数据分析方法（外教版）

发表于 2025-06-02 更新于 2025-08-10 分类于学习阅读次数：本文字数： 101k 阅读时长 ≈ 3:03

数据分析方法（外教版）

课件总结

Week 1

first_week.pdf - 第一周内容回顾与基础

幻灯片内容翻译与概览

幻灯片 1: Stats 201 - 背景检查 (Yes/No 问题)

大家都学过 Stats 210 吗？
我们在 Stats 210 中是否讲授了线性回归？
你了解以下概念吗？
- 估计 (Estimation)
- 假设检验 (Hypothesis testing)
- 置信区间 (Confidence interval)
你听说过线性/二项/泊松回归吗？
气泡备注: 我敢打赌你以为你懂这三个概念。目标是推动你更好地理解它们，而不仅仅是应付考试。它们是任何初级统计/数据科学课程的核心。它们的定义和使用方式塑造了所有早期/传统的从数据中提取信息的方法。

幻灯片 2: 数据分析是关于什么的？

理解一个变量
- 中心或离散程度
理解两个或多个变量
- 它们之间的关系

幻灯片 3: 什么是相关性 (Correlation)？

相关性是衡量两个变量线性相关的程度。
皮尔逊系数 ρX,Y=σXσYcov(X,Y)=σXσYE[(X−μx)(Y−μy)]

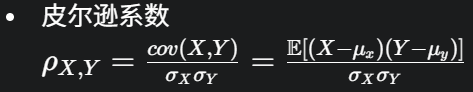
幻灯片 4: 那么关联性 (Association) 呢？相关性 vs 关联性

(图示展示了不同类型的相关性和关联性散点图：强正相关、弱正相关、关联（曲线）、无关联；强负相关、弱负相关、关联（曲线）、无关联)
- 要点: 相关性主要指线性关系，而关联性是更广泛的概念，可以包括非线性关系。

幻灯片 5: 那么因果关系 (Causality) 呢？相关性/关联性 vs 因果关系

(图示：无关联；关联；相关性；因果关系)
(示例图：炎热干燥的夏天天气可能同时导致冰淇淋销量增加和晒伤人数增加。冰淇淋销量和晒伤人数之间可能存在相关性，但它们之间不一定是直接的因果关系，而是都由天气这个共同因素引起。)
- 要点: 相关性或关联性不等于因果关系。

幻灯片 6: 快速回顾

第1章: 介绍，术语，符号 (对应教材 STATS201 book SWU 2023.pdf 第1章)
第2章: 线性模型 - 基础 (对应教材 STATS201 book SWU 2023.pdf 第2章)
第3章: 零模型 vs t检验 (对应教材 STATS201 book SWU 2023.pdf 第3章)

幻灯片 7: 真伪判断题

(题目及解析见后续单独整理的文档)

幻灯片 8: 多项选择题

(题目及解析见后续单独整理的文档)

幻灯片 9: 简答题 (R输出解读)

(题目及解析见后续单独整理的文档)
R输出截图: 展示了一个简单线性回归 summary(lm(y~x)) 的结果，包括：
- Call: 模型公式。
- Residuals: 残差的最小值、第一四分位数、中位数、第三四分位数、最大值。
- Coefficients:
  - (Intercept) (截距) 和 x (斜率) 的估计值 (Estimate)、标准误 (Std. Error)、t值 (t value)、p值 (Pr(>|t|))。
  - 显著性代码 (Signif. codes)。
- Residual standard error: 残差标准误，自由度。
- Multiple R-squared: R平方 (决定系数)。
- Adjusted R-squared: 调整后的R平方。
- F-statistic: F统计量，自由度，p值 (用于检验整个模型的显著性)。

幻灯片 10: 什么是置信区间 (Confidence Interval)？

置信区间 (CI) 是对未知参数的一系列估计。
参数未知但固定，也就是说，它不是随机的！
CI 是在一定的置信水平下根据不确定性计算出来的。
理论结果 - 抽样分布:
- 假设误差项 ϵi∼iidNormal(0,σ2) (注意幻灯片中 σ 未平方，但标准理论中误差项方差为 σ2)。
- β^0∼Normal(β0,σ0)，其中 σ0=σ2(n1+∑(xi−xˉ)2xˉ2)。
- β^1∼Normal(β1,σ1)，其中 σ1=∑(xi−xˉ)2σ2。
- 当 σ 未知时，使用 t 分布：
  - σ^0β^0−β0∼tn−2
  - σ^1β^1−β1∼tn−2
  - σ^2=n−21∑(yi−y^i)2 (残差方差的无偏估计)。

幻灯片 11: 回顾检验与置信区间的二分法

(图示：标准正态/t分布图，中间是接受域，两边黄色区域是拒绝域，对应于双边检验。)
气泡备注 (关于“零模型的置信区间是否总比简单线性模型的置信区间窄”的问题): 错误。虽然实践中通常如此，但理论上可以构建反例。零模型的标准误（用于估计总体均值 μY 的CI）是 s/n。简单线性模型中对条件均值 E[Y∣x0] 的预测的标准误是 sn1+∑(xi−xˉ)2(x0−xˉ)2。当 x0 远离 xˉ 或 x 的散布程度小时，SLR的CI可能更宽。

幻灯片 12: 真伪判断题

(题目及解析见后续单独整理的文档)

幻灯片 13: 不确定性 (Uncertainty)

(图示1：相同置信水平，不同估计量。估计量 μ2 的置信区间比 μ1 的宽，表明 μ2 的不确定性更大。)
(图示2：相同估计量，不同置信水平。99% 置信区间比 95% 置信区间宽。)

幻灯片 14: 多项选择题

(题目及解析见后续单独整理的文档)

知识点梳理 (first_week.pdf)

这份第一周的课件主要是对统计学基础知识进行回顾和铺垫，特别是针对线性回归的核心概念。

统计推断三大基石:
- 估计 (Estimation): 对未知总体参数进行估计，包括点估计和区间估计。
- 假设检验 (Hypothesis Testing): 根据样本信息判断对总体的某个假设是否成立。强调了p值的正确定义：在原假设为真的前提下，观察到当前样本或更极端结果的概率。
- 置信区间 (Confidence Interval): 提供参数估计的一个区间范围，并伴随一个置信水平。其频率学派解释是：如果重复抽样多次并构造多个这样的区间，那么大约有（例如）95%的区间会包含真实的参数值。参数本身是固定的，区间是随机的。
变量间关系:
- 数据分析目标: 理解单个变量的分布特征（中心、离散度）和多个变量之间的关系。
- 相关性 (Correlation): 特指两个变量间的线性关系强度和方向，常用皮尔逊相关系数衡量。
- 关联性 (Association): 比相关性更广泛，包括线性和非线性关系。
- 因果关系 (Causality): 强调相关不等于因果，需要警惕混淆变量和 spurious correlation（伪相关）。
简单线性回归 (SLR) 核心概念:
- 模型假设: Yi=β0+β1xi+ϵi，其中误差项 ϵi 独立同分布于 N(0,σ2)。这是理解和正确应用SLR的前提。
- R输出解读:
  - summary(lm_object) 提供了系数估计、标准误、t统计量、p值、R平方、F统计量等关键信息。
  - 统计显著性: 通常通过斜率 β1 的p值判断。若p值小于预设的显著性水平（如0.05），则认为解释变量与响应变量之间存在显著的线性关系。
  - 实际显著性: 除了统计显著性，还需要考虑效应的大小（如斜率的绝对值）和模型的解释能力（如R平方）在特定应用场景下是否有实际意义。
- 参数估计的抽样分布与置信区间:
  - β^0 和 β^1 的抽样分布在理论上是正态的（或当 σ2 用样本估计时为t分布）。
  - 置信区间公式基于这些抽样分布。
置信区间的性质:
- 置信区间的宽度受置信水平、样本量和数据变异性的影响。
- 更高的置信水平（如99% vs 95%）会导致更宽的置信区间。
- 更大的不确定性（如更大的标准误）会导致更宽的置信区间。

与R代码和教材的联系:

lecture_1.R 中的 t.test(), cor(), lm(), summary(), confint(), predict() 等函数操作都与本周课件回顾的概念直接相关。
教材 STATS201 book SWU 2023.pdf 的第1章（线性回归入门）、第2章（简单线性回归基础）和第3章（零模型与t检验的等价性）是本周回顾内容的详细展开。

这部分内容为后续学习更复杂的模型打下了坚实的基础，强调了对基本统计概念的准确理解和对模型假设的重视。

Week 2

幻灯片内容翻译与概览

幻灯片 1: (概率与参数估计的思考题 - 续)

(牌堆示例图，与 first_week.pdf 幻灯片1类似，继续探讨随机性、固定参数和概率的概念。)
- 文字: "你可能认为两者都是随机的，相应的概率也可以定义为p值。但回想一下，我们假设一个是未知但固定的。"
- 牌桌:
  - 双方随机 (Both Random): P(T=K)=1/13 (老师抽到K的概率)
  - 双方固定 (Both fixed): P(T=K∣T=K)=1 (老师是K，已知老师是K的概率)
  - 一个随机，一个固定 (One random, one fixed): P(Same∣T=K,S=Q)=0 (老师是K，学生是Q，牌面相同的概率)
  - 一个随机，一个未知但固定 (How about 1 random and 1 unknown but fixed?): 这是统计推断的核心情景，我们观察随机样本，推断固定的总体参数。
- "After" vs "Before": 暗示了数据观察前后对参数认识的改变（从先验到后验的贝叶斯思想，或频率学派中参数固定但我们通过数据估计它）。
- 核心问题: "理解潜在的随机性从何而来。" (通常来自抽样过程和个体变异)。

幻灯片 2: (置信区间的频率学派解释 - 续)

(与 first_week.pdf 幻灯片2类似的图示，多条置信区间围绕着真实的总体均值，有的包含有的不包含。)
- 文字: "样本均值 (sample mean) -> 置信区间 (Confidence Interval) -> 包含真实均值 (includes true mean) / 不包含真实均值 (misses true mean)"
- 文字: "真实的总体均值 (TRUE population mean)"
- 文字: "新样本均值 (new sample mean) -> 新置信区间 (new CI)"

幻灯片 3: 线性模型 - 在重复抽样下

(一个从左到右的红色粗箭头，象征着从数据收集到模型建立再到推断的整个过程，是在“重复抽样”的理论框架下进行的。)
- 文字: "进行实验 (Conduct experiment) -> 收集数据 (Collect data) -> 找到一些有意义的数字 (Find some meaningful numbers) -> 计算均值 (Compute mean) -> 计算置信区间 (Compute CI)"

幻灯片 4: 关键组成部分是什么？

(与 first_week.pdf 幻灯片4和 fourth_week.pdf 幻灯片1类似的流程图，再次强调线性模型的构成要素。)
- 数据 (Data) -> 参数估计 (β^0,β^1,…) -> 置信区间 (Confidence Interval) / 假设检验 (Hypothesis Testing) / 估计 (Estimation)
- 数据 (Data) + 模型 (Model) -> (加入新数据 (New Data)) -> 预测 (Prediction) / 预测区间 (Prediction Interval)
- 估计方法: 最大似然 (Maximum Likelihood) / 最小二乘法 (Least-squares)
- 假设 (Assumptions) (例如：误差独立同正态分布，线性，方差齐性) -> 检查假设的工具和违反假设时的补救措施 (Tools to check assumptions and remedies for assumption violations)

幻灯片 5: 什么是分类变量？

分类变量是具有两个或多个互斥类别的变量。
例如：
- 一个是/否的二元变量。
- 水果类型的变量。
- 年龄组的变量。
通常没有内在顺序，即名义变量 (nominal)。
- 名义变量是没有明确顺序的变量。
如果有明确顺序，则称为有序变量 (ordinal)。
气泡备注: 本课程我们只处理名义分类变量。

幻灯片 6: 一个分类预测变量 - 模型结构是什么？

线性模型: Yi∼Normal(μi,σ)
对比:
- 数值预测变量 x: μi=β0+β1xi
  - x 每变化一个单位，Y的均值变化 β1 个单位。
- 二元预测变量 z (0/1编码): μi=β0∗+β1∗zi
  - 这等价于：
    - 当 zi=0 时, μi=β0∗ (基准组均值)
    - 当 zi=1 时, μi=β0∗+β1∗ (另一组均值)
  - β1∗ 代表 z=1 (如"Yes") 相对于 z=0 (如"No") 对截距的额外影响，即两组均值之差。
  - 文字: "当z为Yes（即z=1）而不是No时，会在截距上增加一个额外的分量。"

幻灯片 7: 幂律线性模型 - 解释

回顾对数线性模型 log(Yi)=β0+β1xi+ϵi, 其中 ϵi∼iidNormal(0,σ2):
- 模型可以写成 μlog(y)=β0+β1x，则 Y 的中位数 median(Y)=eβ0+β1x=eβ0eβ1x。
- x 每增加一个单位， Y 的中位数乘以 eβ1 (即增加 100×(eβ1−1) )。
回顾对数-对数 (幂律) 模型 log(Yi)=β0∗+β1∗log(xi)+ϵi, 其中 ϵi∼iidNormal(0,σ2):
- 模型可以写成 μlog(y)=β0∗+β1∗log(x)，则 Y 的中位数 \text{median}(Y) = e^{\beta_0^} x^{\beta_1^} = \alpha x^{\beta_1^*}。
- 如果 x 变为 1.01x (增加1%)，则新的中位数与原中位数的比值为 \frac{\alpha (1.01x)^{\beta_1^ } } {\alpha x^{\beta_1^ } } = 1.01^{\beta_1^*}。
- 根据泰勒展开，1.01^{\beta_1^} \approx 1 + \beta_1^ \times 0.01。
- 所以，x 每增加1%， Y 的中位数大约增加 β1∗。

幻灯片 8: 简单线性模型 - 模型方程、斜率的CI、均值和个体Y的CI/PI (复习)

模型: Yi=β0+β1xi+ϵi, xi是数值型, ϵi∼iidNormal(0,σ2)。
R代码: fit = lm(y~x, data=df), confint(fit)。
- 斜率置信区间解释: "我们估计 x 每增加一个单位， y 的均值变化在 -0.24 到 0.12 之间。" (示例数据)
预测: new.df = data.frame(x=1), predict(fit, new.df, interval="confidence") 和 predict(fit, new.df, interval="prediction")。
- 均值置信区间和个体预测区间解释: "我们估计当 x=1 时，y 的均值在 -0.35 到 0.17 之间，而一个特定的 y 值在 -1.84 到 1.66 之间。" (示例数据)

幻灯片 9: 分类预测变量 (二元) (复习)

模型: Yi=β0+β1zi+ϵi, zi是二元变量, ϵi∼iidNormal(0,σ2)。
二元变量系数的CI解释: "我们估计 z 为1/是 (Yes) 而不是否 (No) 会使得 y 的均值增加 -0.55 到 0.13 个单位。" (示例数据)
均值和个体Y的CI/PI解释: "我们估计当 z=1 时，y 的均值在 -0.37 到 0.12 之间，而一个特定的 y 值在 -1.86 到 1.61 之间。" (示例数据)

幻灯片 10: 二次模型 (复习)

模型: Yi=β0+β1xi+β2xi2+ϵi, xi是数值型, ϵi∼iidNormal(0,σ2)。
用途: 通常用于处理由于非线性关系导致的拟合不足。
系数的CI解释不那么直接有意义。
均值和个体Y的CI/PI解释方法保持不变。
R代码: fit = lm(y ~ x + I(x^2), data=df)。
均值和个体预测区间解释: "我们估计当 x=1 时，y 的均值在 -0.35 到 0.18 之间，而一个特定的 y 值在 -1.84 到 1.67 之间。" (示例数据)
气泡备注: 你不仅需要单独理解第8至14页（此处指幻灯片编号）的解释。但也需要能将其扩展到混合情况，例如乘法模型中的二次项，或对数线性模型中的分类变量等。

幻灯片 11: 乘法对数线性模型 (复习)

模型: log(Yi)=β0+β1xi+ϵi, xi是数值型, ϵi∼iidNormal(0,σ2)。
斜率的CI解释 (反转换后): "我们估计 x 每增加一个单位， y 的中位数增加 -41.6% 到 36.5%。" (示例数据)
中位数和个体Y的CI/PI解释 (反转换后): "我们估计当 x=1 时，y 的中位数在 0.12 到 0.43 之间，而一个特定的 y 值在 0.0036 到 14.45 之间。" (示例数据)

幻灯片 12: 乘法对数线性模型 (含分类变量) (复习)

模型: log(Yi)=β0+β1zi+ϵi, zi是二元变量, ϵi∼iidNormal(0,σ2)。
系数的CI解释: "我们估计 z 为1/是 (Yes) 而不是否 (No) 会使得 y 的中位数增加 -67.6% 到 66.6%。" (示例数据)
中位数和个体Y的CI/PI解释: "我们估计当 z=1 时，y 的中位数在 0.12 到 0.40 之间，而一个特定的 y 值在 0.0035 到 13.86 之间。" (示例数据)

幻灯片 13: 幂律模型 (Log-log) (复习)

模型: log(Yi)=β0+β1log(xi)+ϵi, xi是正数值型, ϵi∼iidNormal(0,σ2)。
斜率的CI解释: "我们估计 x 每增加一个百分比， y 的中位数大约增加 -0.20% 到 0.19%。" (示例数据)
中位数和个体Y的CI/PI解释: "我们估计当 x=1 时，y 的中位数在 0.16 到 0.42 之间，而一个特定的 y 值在 0.0041 到 16.05 之间。" (示例数据)

幻灯片 14: Log-log模型的近似解释 (复习)

"x 增加1% 导致 y 的中位数大约增加 β1 " 这个解释是基于泰勒展开的近似：1.01β1−1≈β1×0.01。
当变化较大时（如 x 增加50%），不应使用此近似。应计算 1.5β1−1。

幻灯片 15: 什么是交互作用 (Interaction)？ (复习)

“交互作用”描述了一个变量 z 改变了另外两个变量 y 和 x 之间关系的情况。
(图示1：空气温度和物种对体温的交互作用 - 不同物种体温随空气温度变化的趋势线不平行。)
(图示2：加糖后时间和搅拌对咖啡甜度的交互作用 - 搅拌会加速糖溶解，从而改变甜度随时间变化的曲线。)

幻灯片 16: 线性模型 - 二元变量z (交互作用的引入) (复习)

假设数值变量 y 和 x 之间的关系取决于二元变量 z。
最简单的方法是使用两个模型 (等价于一个包含交互作用的单一模型): Yi={β0+β1xi+ϵiif zi=0, (β0+β2)+(β1+β3)xi+ϵiif zi=1, 这等价于 Yi=β0+β1xi+β2zi+β3xizi+ϵi。其中 β2 是截距的差异，β3 是斜率的差异。

知识点梳理 (second_week.pdf)

这份第二周的课件主要是对第一周介绍的各种线性模型形式（简单线性、含分类变量、二次项、对数转换、幂律模型）进行系统性的复习和总结，重点在于模型方程的统一理解和参数解释的规范化，并再次强调了交互作用的概念。

统计推断的本质与随机性:
- 通过“抽牌”的例子，引导学生思考统计推断中“未知但固定”的参数与“随机”的样本数据之间的关系，强调理解随机性的来源是正确进行统计推断的基础。
- 再次通过图形展示置信区间的频率学派含义：多次重复实验，置信区间会围绕真实参数波动，其中一定比例（如95%）的区间会包含该参数。
线性模型的通用框架与关键组件:
- 重申了线性模型分析的基本流程：从数据出发，通过参数估计（如最大似然、最小二乘）建立模型，然后进行假设检验、置信区间估计、预测等。
- 强调了模型假设的重要性，以及检查假设和处理违规情况的必要性。
分类预测变量的模型结构:
- 明确了名义分类变量和有序分类变量的区别，并指出本课程主要关注名义分类变量。
- 详细解释了当模型中包含一个二元分类预测变量（如0/1编码）时，模型 μi=β0∗+β1∗zi 中，β0∗ 代表基准组的均值，β1∗ 代表另一组相对于基准组的均值差异。
各种线性模型形式的解释范式总结:
- 简单线性模型 (Y∼Xnumeric): 解释斜率 β1 对 Y 均值的影响。
- 含二元分类变量的模型 (Y∼Zbinary): 解释指示变量系数 β1 对 Y 均值的差异影响。
- 二次模型 (Y∼X+X2): 重点在于描述曲线关系和进行预测，单个系数的解释意义不大。
- 对数线性模型 (log(Y)∼Xnumeric): 解释 X 的单位变化对 Y 中位数的乘性影响或百分比变化。
- 对数线性模型 (含分类变量 log(Y)∼Zbinary**): 解释分类变量不同水平下 Y 中位数的比率或百分比差异**。
- 幂律模型 (log(Y)∼log(Xnumeric)): 解释 X 的百分比变化对 Y 中位数的百分比变化的影响（弹性概念）。强调了1%近似解释的局限性，对于较大百分比变化需要精确计算。
交互作用的再强调:
- 再次定义交互作用：一个变量改变了另外两个变量之间的关系。
- 通过代数形式解释了包含一个数值变量和一个二元分类变量的交互作用模型，说明它等价于为分类变量的每个水平拟合一条具有不同截距和斜率的直线。

与R代码和教材的联系:

本周课件内容是对 lecture_1.R 到 lecture_6.R 中涉及的各种模型解释方法的一个高度概括和对比总结。
它系统性地对应了教材 STATS201 book SWU 2023.pdf 中第1-8章关于不同线性模型形式的解释部分。例如，第1、2章的简单线性回归，第4章的曲线拟合（二次模型），第5章的二元分类变量，第6章的乘法模型（对数线性），第7章的幂律模型，以及第8章的交互作用模型。

这份课件的核心价值在于提供了一个统一的框架来理解和解释不同类型的线性模型及其变体，帮助学生巩固之前学习的知识点，并为后续更复杂的模型（如多重回归、GLM）做好准备。它强调了不仅要会拟合模型，更要会正确地解释模型结果。

Week 3

幻灯片内容翻译与概览

幻灯片 1: 执行摘要 (Executive Summary) - 示例1 (Exam vs Test & Attendance 交互模型 - 复习)

我们想要量化学生的考试分数与出勤率和测试分数之间的关系。
测试分数和考试分数之间存在明显的线性关系，但这种关系在规律出勤和非规律出勤的学生之间有所不同。
我们估计，非规律出勤学生每额外获得一分测试分数（满分20分），其期望考试分数将增加1.8到3.7分。
对于规律出勤的学生，每测试分数对应的期望考试分数额外增加0.04到2.2分。
$^+$ 由于两组的斜率不同，我们需要单独讨论每个斜率。

幻灯片 2: 方法与假设检查 (Method and Assumption Checks) - 示例1 (复习)

由于我们有两个解释变量，一个是数值型，一个是因子型，我们拟合了一个线性模型，该模型为每个出勤组使用了不同的截距和斜率（即交互作用模型）。
所有模型假设均得到满足。
我们不能移除交互作用项 (P值 = 0.043)。
我们的最终模型解释了学生考试分数变异性的63%（中等程度），其形式为： Exami=β0+β1×Testi+β2×Attendi+β3×Attendi×Testi+ϵi, 其中 Attendi=1 如果学生 i 规律出勤，否则为0，并且 ϵi∼iidN(0,σ2)，β0,β1,β2,β3 是固定但未知的参数。

幻灯片 3: (奥卡姆剃刀与模型复杂度 - 复习)

当样本量相对较小时，我们常常面临两个或多个具有相似解释能力模型的情况。
我们更喜欢一个更简单的模型，即具有较少假设/参数的模型。
复杂性就像构建模型的成本。我们知道总能实现完美拟合，即饱和模型，但这将耗费一切！
一个好的模型应该始终平衡拟合优度和复杂性。
当面临具有相似解释能力模型时，最终取决于成本。
核心思想: 假设、限制和变量数量。数据大小。奥卡姆剃刀支持更简洁（优雅）的解决方案，该方案能持续解释我们现在观察到的现象。保持简单 (Keep it simple!)
(图示：地心说 vs 日心说，日心说模型更简单且解释力更强。)

幻灯片 4: 方法与假设检查 - 示例2 (Thyroid drug experiment - 无交互作用，最终简化模型 - 复习)

探索性图表建议，为解释小鼠甲状腺重量，我们首先拟合了包含解释变量药物治疗和体重的线性模型及其交互作用。但交互作用项不显著 (P值=0.11)。
移除了交互作用项后重新拟合模型。然而，治疗效应不显著 (P值=0.37)，因此也被移除。
小鼠被随机分配到各组，测量是相互独立的。
所有其他模型假设均得到满足。一个潜在的影响点被调查过，但考虑到其位置以及该数据集极小的规模（16个观测值），我们将忽略它。
我们的最终模型是 thyroidi=β0+β1×weighti+ϵi，其中 ϵi∼iidN(0,σ2)，β0,β1 是固定但未知的参数。
我们的模型解释了甲状腺重量变异性的大约82%。

幻灯片 5: 执行摘要 - 示例2 (复习)

我们想要评估一种新开发的旨在增加甲状腺重量（毫克）的药物的效果。
我们唯一能报告的是，体型较大的小鼠拥有较大的甲状腺。我们可以报告这种效应的大小，但由于它不是研究问题的一部分，所以我们不这样做。
我们没有证据相信这种药物能增加小鼠甲状腺的期望大小。

幻灯片 6: 什么是 Anova (方差分析)？

Analysis of Variance (方差分析)
它基于分解响应变量的方差。
它可以用来“削减 (shave)”我们的模型，即决定我们是否可以移除一个变量。

幻灯片 7: 为什么不（总是）使用T检验？ (在多重回归/ANOVA情境下)

(R代码示例：y ~ x * z，其中x是数值，z是二元(0/1)指示变量)
- x = rnorm(100); z = c(rep(0, 50), rep(1, 50))
- y = 0.5 + 0.1*x + rnorm(100, sd = 0.1) (注意这里生成y时没有包含z或x:z的效应，所以理论上z和x:z的系数应为0)
- df = data.frame(y=y, x=x, z=z)
- summary(lm(y ~ x*z, data=df))
(输出 summary() 的 Coefficients 部分，显示了 (Intercept), x, z, x:z 的t检验结果。在这个模拟数据中，z 和 x:z 的p值可能会随机地显得显著或不显著。)
气泡备注 (指向 x:z 的t检验): 在这种情况下 (指交互作用项只有一个参数，如两个二元因子或一个数值一个二元因子的交互)，T检验足够了。
批注 (指向所有系数的t检验): 这些T检验中的每一个都在测试，在模型中存在其他系数的情况下，该系数是否为零。

幻灯片 8: 一次削减一个beta (模型简化过程 - 基于t检验)

(R代码示例：summary(lm(y ~ x+z, data=df))，即从 x*z 模型中移除了不显著的交互作用项 x:z 后的模型)
(输出显示 z 的t检验不显著)
文字: “下一步是削减掉z。”
(圈出 Multiple R-squared: 0.4819)
文字: “R平方之前是0.4829” (指包含交互作用时，移除不显著项对R平方影响很小，但调整R平方可能提高，自由度增加)。

幻灯片 9: 无论哪种方式，结论相同 (关于移除顺序)

(R代码示例：summary(lm(y ~ x + x:z, data=df))，这是一个不寻常的模型形式，包含了 x 和 x:z 但没有 z 的主效应。通常不推荐这样做，除非有强理论依据。标准做法是遵循层次原则，如果包含交互项，则其组成的主效应也应包含在内。)
(输出显示 x:z 的t检验不显著)
文字: “下一步是削减掉交互作用项。” (这与幻灯片7的结论一致，即交互作用不显著)

幻灯片 10: 根据奥卡姆剃刀

(R代码示例：summary(lm(y ~ x, data=df))，进一步简化模型，只剩下x，假设之前的步骤已确定z和交互作用均不显著。)
文字: “这是一个更好的模型。” (前提是简化是合理的)

幻灯片 11: 超过两个类别 (多水平因子)

(R代码示例：创建一个有3个水平(0,1,2)的因子z，并拟合 lm(y ~ z, data=df))
- z = c(rep(0, 25), rep(1, 25), rep(2, 50))
- y = 1 + ifelse(z==2, 0.1, 0) + rnorm(100, sd = 0.1) (这里生成y时，z=0和z=1的均值相同，z=2的均值高0.1)
- df = data.frame(y=y, z=factor(z))
- summary(lm(y~z, data=df))
(输出 summary() 显示了 (Intercept) (对应z=0的均值)，z1 (z=1与z=0的均值差)，z2 (z=2与z=0的均值差) 的t检验结果。)
文字 (指向 z1 的p值 (0.339) 和 z2 的p值 (1.43e-06)): “对于z是否有用，没有总体结论！” (因为一个比较不显著，一个显著，t检验无法告诉我们z这个因子作为一个整体是否有用。)
文字 (指向右侧): “我们想要检验 H0:β~1=β~2=0” (这里 β~1,β~2 指的是与因子z相关的参数，即 z1 和 z2 的系数，暗示需要一个整体检验，即F检验。)

幻灯片 12: 如果组间均值的变异性很大，z可能有用

(图示：Y对Z的条状图/散点图，显示了三组(z=0,1,2)的均值 yˉ0,yˉ1,yˉ2 和总体均值 yˉ )
组间方差 (Between-group variance): VarBetween=k−11∑j=1k(yˉj−yˉ)2 (这里k是组数，幻灯片用3-1)

幻灯片 13: 如果组内均值的变异性很小，z可能有用

(与幻灯片12类似的图示)
组内方差 (Within-group variance): VarWithin=N−k1∑j=1k∑i=1nj(yij−yˉj)2 (N是总样本量, nj是第j组样本量)
F统计量: F=VarWithinVarBetween (更准确地说是 MSBetween/MSWithin，均方)

幻灯片 14: F检验在summary输出中 (针对整个模型) vs anova()

(幻灯片11中 summary(lm(y~z, data=df)) 的完整输出)
F-statistic: 16.23 on 2 and 97 DF, p-value: 8.336e-07。这个F检验是针对整个模型（即因子z作为一个整体）是否显著的检验。
文字 (指向p值): “检验 H0:β1=β2=0 的p值” (这里 β1,β2 指的是与因子z的非基准水平相关的系数)。
结论: F检验回答了一个特定的系数集合是否同时为零的问题。它回答了一个模型/分类变量是否有用的问题。

幻灯片 15: F对于F值多大才算大？ (F分布)

可以证明F比率/F统计量服从F分布。
F分布由两个参数 d1 (分子自由度) 和 d2 (分母自由度) 定义。
为了判断因子z是否有用 (对于单因素ANOVA):
- d1=类别数−1
- d2=总数据点数−类别数
有了F统计量的分布，我们就可以正式检验 H0:β1=β2=⋯=βk=0 (k是与因子相关的非基准水平系数个数)。

幻灯片 16: 一般的F检验 (使用 anova() 函数)

anova(lm(y~z, data=df)) 输出显示因子 z (作为一个整体) 的F检验结果，与 summary() 中的F检验结果一致（对于单因子模型）。
anova(lm(y ~ z*x, data=df)) (幻灯片中为 y ~ z+x+z:x，应理解为包含交互作用的模型) 输出序贯方差分析表 (Type I SS)。
- 在这种表中，每个项（如 z, x, z:x）的F检验是在调整了模型中位于它前面的项之后进行的。因此，变量进入模型的顺序会影响其F检验的P值。

幻灯片 17: (解释变量的变异性对斜率估计稳定性的影响 - 复习)

简单线性模型中，斜率的标准误 SE(β^1)=∑(xi−xˉ)2σ。
如果解释变量 xi 的散布程度 (∑(xi−xˉ)2) 很小（即 xi 值非常集中），则 SE(β^1) 会很大，导致 β^1 的估计非常不稳定。
(图示：左图显示解释变量 xi 变异性小，多次抽样得到的回归线非常不稳定。右图显示解释变量 xi 变异性大，回归线相对稳定。)

幻灯片 18: (多重共线性简介 - 复习)

一般来说，解释/预测变量的配置可能会导致多重共线性 (multicollinearity)，从而影响模型/估计量标准误的稳定性。
当模型中有多个数值解释变量 x 和 z 时，它们之间的相关性会影响模型的稳定性。

知识点梳理 (third_week.pdf)

这份第三周的课件重点回顾和深化了模型选择的策略，特别是奥卡姆剃刀原则的应用，并详细介绍了方差分析 (ANOVA) 和 F检验在评估多水平因子变量或一组解释变量整体显著性时的核心作用。同时，它也再次提及并强调了多重共线性对模型稳定性的潜在影响。

模型选择与奥卡姆剃刀 (Occam's Razor):
- 原则: 在多个具有相似解释能力的模型中，应选择最简单的那个（即参数最少的）。强调了在拟合优度和模型复杂性之间进行权衡。
- 实践: 通常通过逐步移除模型中不显著的项（基于t检验或F检验的p值）来简化模型。
- 示例: 课件通过甲状腺药物实验的案例（从交互作用模型逐步简化到仅含体重的主效应模型）和模拟的R代码 (y ~ x*z -> y ~ x+z -> y ~ x) 演示了这一过程。
- 对应教材 STATS201 book SWU 2023.pdf 第9章 (第14-20页) 的模型选择部分。
方差分析 (ANOVA) 与 F检验:
- ANOVA的本质: 将响应变量的总变异分解为由不同解释变量（或因子水平）引起的变异和残差变异。
- F检验的用途:
  - 检验多水平因子的整体显著性: 当一个分类解释变量有三个或更多水平时，summary()输出中对各指示变量的t检验只能说明该水平与基准水平的差异是否显著，而不能判断该因子变量作为一个整体是否对响应变量有显著影响。此时需要F检验（通常由anova()函数或summary()输出中的F-statistic提供）来检验与该因子相关的所有系数是否同时为零。
  - 检验交互作用的整体显著性: 对于包含多个因子或数值与因子交互作用的模型，F检验可以评估整个交互作用部分的显著性。
  - 比较嵌套模型: F检验可以用来比较一个复杂模型和一个简化模型（复杂模型的子集），判断移除的项是否显著影响模型的拟合优度。
- F统计量的构造: 其基本思想是比较组间（或模型解释的）变异与组内（或残差）变异。F统计量服从F分布，其形状由分子自由度 (df1) 和分母自由度 (df2) 决定。
- anova() 函数: 在R中，anova(lm_object) 会生成一个方差分析表。对于包含多个解释变量的模型，它通常给出的是序贯F检验 (Type I Sum of Squares)，这意味着变量进入模型的顺序会影响其F检验的p值。
- 对应教材 STATS201 book SWU 2023.pdf 第9章 (第18, 23页) 和第11章 (第12页) 关于 anova() 的使用。
解释变量的配置与模型稳定性:
- 再次强调了简单线性回归中解释变量 x 的散布程度 (∑(xi−xˉ)2) 对斜率估计稳定性的重要性。如果 x 的值域很窄，斜率估计的标准误会很大。
- 引出了多重共线性的概念：当模型中存在多个解释变量，并且它们之间高度相关时，会导致参数估计不稳定，标准误增大，难以解释单个变量的独立效应。

与R代码和教材的联系:

lecture_7.R 中的教学方法案例 (teach.df) 完美地演示了从交互作用模型开始，通过 anova() 检验交互作用，然后简化到主效应模型，并使用 relevel() 进行不同基准的比较，这些都与本周课件的核心内容一致。
lecture_8.R 中的婴儿出生体重案例，虽然主要目标是多重回归，但也涉及了模型简化和变量选择的思想。
教材 STATS201 book SWU 2023.pdf 第9章（不含交互作用的模型）和第11章（单因素ANOVA）是本周课件的主要理论和实践依据。

这份课件通过回顾、实例和理论讲解，帮助学生理解模型选择的逻辑，掌握使用F检验评估因子和交互作用整体效应的方法，并初步认识到解释变量间关系对模型稳定性的影响。

Week 4

幻灯片内容翻译与概览

幻灯片 1: 回顾线性模型

(与 second_week.pdf 幻灯片4类似的流程图，展示线性模型的各个组成部分和流程。)
- 数据 (Data) → 参数估计 (β^0,β^1,…) → [置信区间 (Confidence Interval) / 假设检验 (Hypothesis Testing) / 估计 (Estimation)]
- 数据 (Data) + 模型 (Model) → (加入新数据 (New Data)) → [预测 (Prediction) / 预测区间 (Prediction Interval)]
- 估计方法: 最大似然 (Maximum Likelihood) / 最小二乘法 (Least-squares)
- 假设 (Assumptions): Yi=β0+β1xi+ϵi, ϵi∼iidN(0,σ2); 线性性 (Linearity); 方差齐性 (EOV / Constant Variance); 正态性 (Normality)。

幻灯片 2: 假设检验与置信区间的局限性

显著性水平（例如，通常为5%或95%水平）仅适用于单个检验或估计，而不适用于一系列检验或估计。(多重比较问题)
仅当该估计或检验不是由数据本身所启发或建议时，它们才是合适的。(数据窥探/p-hacking问题)
气泡备注: 回想一下课堂上的两个模拟研究 (可能指第一类错误率的膨胀和数据驱动的假设)。

幻灯片 3: 关于二项分布、正态分布、泊松分布的故事

棣莫弗关于赌博问题的研究引出了第一个钟形曲线（正态分布的早期形式，作为二项分布的近似）。
伽利略到高斯关于天文观测中误差的研究（误差理论，正态分布）。
二项分布 (Binomial): P(Y=y)=(yn)py(1−p)n−y, y∈0,1,...,n (离散)。
正态分布 (Normal): fY(y)=2πσ21exp(−2σ2(y−μ)2), y∈(−∞,∞) (连续)。
中心极限定理 (Central Limit Theorem): 若 Yi 是来自任何分布的独立同分布随机变量，均值为 μ，方差为 σ2，则当 n→∞ 时，它们的和（或均值）∑i=1nYi 近似服从正态分布。
泊松分布 (Poisson): y∈0,1,2,3,.... 泊松的二项分布极限定理得到了泊松分布：若 pn 是一系列在 (0, 1] 之间的实数，使得序列 npn 收敛到一个有限的极限 μ，则 limn→∞(yn)pny(1−pn)n−y=y!μyexp(−μ)。

幻灯片 4: 如果n或均值很小怎么办？

(图1：Normal Vs Poisson (mu=0.5)) 当泊松分布的均值 μ 很小时（如0.5），其分布是高度右偏的，与对称的正态分布差异显著。
(图2：Normal Vs Binomial (n=6, p=0.75)) 当二项分布的试验次数 n 较小，或成功概率 p 接近0或1时，其分布也会偏斜，与正态近似差异较大。

幻灯片 5: 在回归模型中的价值 (普通LM处理非正态数据的局限性)

左图 (Poisson data): 真实数据是泊松分布（随x指数增长的均值）。如果用普通线性模型（如多项式回归，图中红线）去拟合，可能在数据范围内看似可以，但模型形式不正确。蓝线（泊松回归）能更好地捕捉指数趋势。
右图 (Beyond Observed Poisson data): 展示了外推的危险。普通线性模型（红线）在外推时可能产生非常不合理（甚至为负）的预测，而基于正确分布假设的泊松回归（蓝线）外推更为稳健。

幻灯片 6: 解释不同类型的回归模型 (总结)

线性回归模型 (Linear regression model):
- Yi∼Normal(μi,σ2), μi=β0+β1xi.
- 解释: x 每增加一个单位，Y 的均值增加 β1 个单位。
对数线性模型 (Log-linear model, Y取对数):
- log(Yi)∼Normal(μi,σ2), μi=β0+β1xi (这里 μi=E[log(Yi)]).
- 解释: x 每增加一个单位，Y 的中位数乘以 exp(β1) (即增加 100×[exp(β1)−1] )。
幂律模型 (Power Law model, Y和X均取对数):
- log(Yi)∼Normal(μi,σ2), μi=β0+β1log(xi). $Y_i=\beta_0x_i^{\beta_1}$
- 解释: x 每增加1%，Y 的中位数大约增加 β1。
- 幂律模型 (log(Y)∼log(X)): 在这个模型中，解释变量 X 也进行了对数转换。因此，系数 β1 反映的是当 log(X) 发生一个单位变化时，log(Y) 的期望值会发生 β1 的变化。然而，在实际解释中，我们通常更关心原始变量 X 的相对变化（即百分比变化）*所带来的影响。例如，我们想知道当* X *增加1%时，*Y *的中位数会如何变化。如果* X *增加1%，那么新的* X新=X×(1+0.01)=1.01X*。此时，*log(X新)−log(X旧)=log(1.01X)−log(X)=log(1.01)*。根据模型，*log(Y) *的变化量是* Δlog(Y)=β1×Δlog(X)=β1×log(1.01)*。所以，*log(Y中位数,旧Y中位数,新)=β1log(1.01)=log((1.01)β1)*。两边取指数得到* Y中位数,旧Y中位数,新=(1.01)β1****。对于小的百分比变化**** r****（例如**** r=0.01 *代表1%），根据泰勒展开近似，*(1+r)β1≈1+β1r****。因此，*(1.01)β1≈1+β1×0.01*。****
泊松回归模型 (Poisson regression model):
- Yi∼Poisson(μi), log(μi)=β0+β1xi.
- 解释: x 每增加一个单位，Y 的均值乘以 exp(β1) (即增加 100×[exp(β1)−1] )。
Logistic回归模型 (Logistic regression model):
- Yi∼Binomial(ni,pi), logit(pi)=β0+β1xi.
- 解释: (见幻灯片8)
广义线性模型 (GLM) 通式:
- Yi∼某种指数族分布(θi), g(θi)=β0+β1xi (g(⋅) 是连接函数)。

幻灯片 7: Logit - 几率的对数 (Odds 和 Log-Odds)

几率 (Odds): o=O(Y=1)=P(Y=0)P(Y=1)=1−pp。
概率与几率转换: p=o+1o。
对数几率 (Logit): η=Logit(p)=log(o)=log(1−pp)。
Logit的反函数 (Logistic函数): p=1+exp(η)exp(η)。
概率 p∈[0,1] 对应几率 o∈[0,∞)，对应对数几率 η∈(−∞,∞)。

幻灯片 8: 解释包含数值和分类变量的GLM

模型形式 (以包含一个数值变量 xi 和一个二元分类变量 zi 为例，可能还有交互作用): g(θi)=β0+β1xi+β2zi(+β3xizi for interaction)
泊松回归解释:
- 当 z 固定时，x 每增加一个单位，Y 的均值增加 100×[exp(β1)−1]。
- 当 x 固定时，若 z=1 (相比于 z=0)，Y 的均值高出 100×[exp(β2)−1]。
- 交互作用: 当 z=1 时，x 每增加一个单位，Y 的均值增加 100×[exp(β1+β3)−1]。交互作用本身解释复杂，常需结合图形。
Logistic回归解释:
- 当 z 固定时，x 每增加一个单位，Y=1 的几率 (Odds) 增加 100×[exp(β1)−1]。
- 当 x 固定时，若 z=1 (相比于 z=0)，Y=1 的几率高出 100×[exp(β2)−1]。
- 交互作用: 当 z=1 时，x 每增加一个单位，Y=1 的几率增加 100×[exp(β1+β3)−1]。
注意: 当分类变量有三个或更多类别时，应使用ANOVA/卡方检验（针对GLM是偏差分析中的似然比检验或Wald检验的推广）来评估其总体显著性，而不是单个指示变量的z检验（或t检验）。

知识点梳理 (fourth_week.pdf)

这份第四周的课件是广义线性模型 (GLM) 的一个重要总结和扩展，它回顾了线性模型的局限性，引入了GLM处理非正态响应（特别是计数和比例数据）的必要性，并系统地对比了不同模型（包括普通线性模型及其对数转换形式、泊松回归、Logistic回归）的解释框架。

传统线性模型 (LM) 的回顾与局限:
- 再次强调LM的核心假设（误差正态、独立、同方差，关系线性）。
- 指出传统假设检验和置信区间的局限性，特别是多重比较问题（一系列检验会使第一类错误率膨胀）和数据窥探（由数据启发的检验可能导致假阳性）。
常见离散分布及其与正态分布的关系:
- 回顾了二项分布和泊松分布的概率质量函数和适用场景。
- 通过中心极限定理和泊松的二项极限定理建立了它们与正态分布的联系。
- 通过图形清晰展示了当参数（二项分布的n，泊松分布的 $\mu$ ）较小时，这些离散分布与正态近似的差异，强调了在这些情况下直接使用基于正态假设的LM是不合适的。
- 对应教材 STATS201 book SWU 2023.pdf 第13章 (第20-27页) 和第15章 (第4-6页)。
广义线性模型 (GLM) 的引入与优势:
- 动机: 当响应变量是计数（Poisson）或比例/二元（Binomial）时，LM的假设不满足。直接对这类数据使用LM或简单地对其进行对数转换都有其局限性（如log(0)问题，预测值超出范围，方差结构不匹配）。
- GLM结构:
  1. 随机部分: 响应变量 Yi 服从某个指数族分布（如Poisson, Binomial）。
  2. 系统部分: 解释变量的线性组合 ηi=β0+β1xi1+…。
  3. 连接函数 (Link Function) g(⋅): 连接响应变量的期望值 E[Yi]=μi 与线性预测子 ηi，即 g(μi)=ηi。
- 对应教材 STATS201 book SWU 2023.pdf 第13章 (第29-31页) 对GLM的介绍。
特定GLM模型及其解释:
- 泊松回归 (Poisson Regression):
  - 用于计数数据。
  - 连接函数: 对数连接，log(μi)=ηi。
  - 解释: 解释变量每改变一个单位，响应变量的均值 μi 乘以 exp(βj)。
  - 对应教材第13章。
- Logistic回归 (Logistic Regression):
  - 用于二元数据 (0/1) 或比例数据。
  - 连接函数: Logit连接，logit(pi)=log(1−pipi)=ηi。
  - 解释: 解释变量每改变一个单位，事件发生的几率 (Odds) pi/(1−pi) 乘以 exp(βj)。
  - 对应教材第15章。
- 课件系统对比了普通LM、对数转换LM、泊松回归和Logistic回归在解释系数时的不同侧重点（均值 vs 中位数 vs 几率）和形式（加性 vs 乘性）。
包含分类变量和交互作用的GLM解释:
- 当GLM中包含数值和分类解释变量（及其交互作用）时，解释方法与LM中的类似，但需要将效应最终转换回响应变量的原始尺度（均值或几率）的乘性变化或百分比变化。
- 强调了交互作用使得解释变得复杂，通常需要结合具体水平进行描述或可视化。
- 提醒对于多水平分类变量，需要进行整体显著性检验（如偏差分析中的卡方检验或F检验）。

与R代码和教材的联系:

lecture_10.R 和 lecture_11.R 中的代码实例（CRAN数据、地震数据、鲷鱼数据、篮球数据、挑战者号数据、黑线鳕数据）完美地演示了本周课件中介绍的Poisson回归和Logistic回归的应用，包括模型拟合 (glm())、参数解释、过离散处理 (family=quasipoisson 或 quasibinomial)、预测 (predictGLM()) 以及与传统LM的对比。
教材 STATS201 book SWU 2023.pdf 的第13章（泊松模型）、第14章（泊松模型实例）、第15章（二项模型）和第16章（列联表分析）是本周课件内容的详细理论基础和应用案例。

这份课件是整个课程从传统线性模型过渡到更广泛的广义线性模型的关键，它不仅介绍了GLM的理论框架，更重要的是教会学生如何根据数据类型选择合适的模型并正确解释模型结果。

在对数线性模型 (log(Y)=β0+β1X) 和幂律模型（或称对数-对数模型，log(Y)=β0+β1log(X)) 中，虽然响应变量 Y 都进行了对数转换，使得我们关注的是 Y 的中位数的相对变化（乘性或百分比），但由于解释变量 X 的处理方式不同，导致了系数 β1 解释上的核心差异。

辨析原因：

关键在于解释变量 X 在模型中是原始尺度还是对数尺度。

对数线性模型 (log(Y)∼X):

模型中 X 是其原始单位。因此，我们考察的是当 X 发生一个绝对单位的变化时（例如，年龄增加1岁，温度升高1摄氏度），log(Y) 会发生 β1 的变化。

由于 log(Y新中位数)−log(Y旧中位数)=β1，这意味着 log(Y新中位数/Y旧中位数)=β1，所以 Y新中位数/Y旧中位数=exp(β1)。

因此，Y 的中位数会变为原来的 exp(β1) 倍，或者说变化了 (exp(β1)−1)×100。这里解释的是 X 每单位绝对变化对 Y 中位数的乘性或百分比影响。

幂律模型 (log(Y)∼log(X)):

模型中 X 也被取了对数。因此，我们考察的是当 log(X) 发生一个单位变化时，log(Y) 会发生 β1 的变化。log(X) 变化一个单位，近似对应于 X 本身发生一个较大的乘性变化（乘以 e≈2.718 倍）。

然而，在解释幂律模型时，我们更常关注 X 发生一个小的相对百分比变化（例如1%）时的影响。如果 X 增加1%，即 X 变为 1.01X，那么 log(X) 的变化量是 log(1.01X)−log(X)=log(1.01)。

根据模型，log(Y) 的变化量是 β1×Δ(log(X))=β1×log(1.01)。

所以，Y新中位数/Y旧中位数=exp(β1×log(1.01))=(1.01)β1。

对于小的百分比变化（如1%，即0.01），根据泰勒展开近似，(1+r)β1≈1+β1r。所以 (1.01)β1≈1+β1×0.01。

这意味着 Y 的中位数大约变化了 (β1×0.01)×100。这里解释的是 X 每1%的相对变化对 Y 中位数的百分比影响，这个 β1 就是所谓的弹性系数。

总结来说：

在对数线性模型中，由于 X 未取对数，我们解释的是 X 绝对变化一个单位的影响。

在幂律模型中，由于 X 也取了对数，我们通常解释的是 X 相对变化一个百分点的影响。

举例说明：

假设我们研究广告投入 (Advertising, 单位：万元) 对产品销量 (Sales, 单位：万件) 的影响。

如果我们拟合了对数线性模型: log(Sales)=2.5+0.05×Advertising

这里的 β^1=0.05。

解释: 广告投入每增加1万元，产品销量的中位数预计会乘以 exp(0.05)≈1.0513 倍，即大约增加 (1.0513−1)×100。

如果我们拟合了幂律模型 (对数-对数模型): log(Sales)=1.8+0.6×log(Advertising)

这里的 β^1=0.6。

解释: 广告投入每增加1%，产品销量的中位数预计大约会增加 0.6。这意味着销量的广告弹性是0.6。

在这个例子中，两种模型中的系数 0.05 和 0.6 的含义是完全不同的，因为它们对应的是解释变量不同类型的变化（绝对单位变化 vs. 百分比变化）。选择哪种模型取决于我们对变量间关系的理论假设以及数据的实际表现。

题目总结

first week

判断题 (幻灯片 7)

题目: 在假设检验中，如果我们拒绝原假设，那么备择假设必定为真。
- 判断: 错误。
- 解析: 统计推断是基于概率的。拒绝原假设意味着我们有足够的证据表明原假设不太可能为真，因此我们选择相信备择假设。然而，这并不排除我们犯了第一类错误（Type I error），即错误地拒绝了一个真实的原假设。我们永远不能100%确定备择假设为真，只能说数据更支持备择假设。
题目: 在假设检验中，通常所说的p值是原假设为真的概率。
- 判断: 错误。
- 解析: 这是一个非常常见的对p值的误解。p值是在假定原假设（H0）为真的条件下，观察到当前样本统计量或更极端统计量的概率。它衡量的是样本数据与原假设之间的一致性程度，而不是原假设本身为真的概率。
题目: 在假设检验中，通常所说的p值是“如果原假设为真，在重复试验中观察到与我们所见数据一样极端或更极端的数据的概率”。
- 判断: 正确。
- 解析: 这正是p值的准确定义。它描述的是在原假设成立的世界里，我们当前观察到的数据（或比它更不利于原假设的数据）出现的可能性有多大。如果这个可能性很小（即p值很小），我们就倾向于怀疑原假设的真实性。

多项选择题 (幻灯片 8)

题目: 一个简单线性模型的潜在假设是： A. Yi∼Normal(0,σ2) B. Yi=β0+β1xi+ϵi 其中 ϵi∼Normal(0,σ2) C. Yi=β0+β1xi+ϵi 其中 ϵi∼iidNormal(0,σ2) D. Yi=β0+β1xi+ϵi 其中 ϵi∼iidNormal(0,σi2)

正确选项: C
解析:
- A 选项: 错误。该选项描述的是响应变量 Yi 本身服从均值为0的正态分布，这通常不符合实际情况，并且没有体现解释变量 xi 的作用。在线性回归中，我们假设的是误差项 ϵi 服从正态分布。
- B 选项: 错误。虽然正确描述了模型结构和误差项 ϵi 服从均值为0、方差为 σ2 的正态分布，但它遗漏了误差项之间独立同分布 (iid - independently and identically distributed) 的重要假设。
- C 选项: 正确。这个选项完整且准确地表述了简单线性回归模型的核心假设：响应变量 Yi 是解释变量 xi 的线性函数加上一个误差项 ϵi，并且这些误差项是独立同分布的，服从均值为0、方差恒为 σ2 的正态分布。
- D 选项: 错误。σi2 表示误差项的方差随观测值 i 的不同而变化，这描述的是异方差性 (heteroscedasticity)。简单线性回归的标准假设是同方差性 (homoscedasticity)。

简答题 (R输出解读练习) (幻灯片 9)

背景: 给定以下R输出的摘要信息：

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max
-0.44158 -0.12497 -0.01459  0.11600  0.60595

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 99.99212    0.01343  7445.8   <2e-16 ***
x            0.06885    0.01308     5.263  3.68e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1895 on 198 degrees of freedom
Multiple R-squared:  0.1227,    Adjusted R-squared:  0.1183
F-statistic: 27.7 on 1 and 198 DF,  p-value: 3.675e-07

题目: 当 x=0.5 时，给出 y 的预测值。
- 解析:
  - 预测值 y^=β^0+β^1x。
  - 从输出中可知，β^0=99.99212 (截距的Estimate)，β^1=0.06885 (x的Estimate)。
  - 所以，当 x=0.5 时，y^=99.99212+0.06885×0.5=99.99212+0.034425=100.026545。
  - (课件中手写备注的计算 99.9212×0.06885×0.5=3.44 是错误的，它似乎将截距、斜率和x值相乘了，这不符合线性回归的预测方式。)
题目: 判断 x 和 y 之间的线性关系是否统计显著。请说明理由。
- 解析:
  - x 和 y 之间的线性关系是统计显著的。
  - 理由：我们关注解释变量 x 的系数（即斜率 β1）是否显著不为零。原假设是 H0:β1=0。从R输出的 Coefficients 部分可以看到，变量 x 对应的p值 (Pr(>|t|)) 是 3.68×10−7 (即 3.68e-07)。这个p值远小于常见的显著性水平（如 α=0.05, 0.01 或 0.001）。因此，我们有非常强的统计证据拒绝原假设，结论是 x 的系数（斜率）显著不为零，表明 x 和 y 之间存在统计上显著的线性关系。
题目: 判断 x 和 y 之间的线性关系是否实际显著。请说明理由。
- 解析:
  - 判断实际显著性需要结合具体情境和领域知识，仅从统计输出无法直接给出明确的“是”或“否”的答案。
  - 理由：
    - 统计显著性: 如上所述，关系是统计显著的。
    - 效应大小 (Effect Size): 斜率的估计值 β^1=0.06885。这意味着 x 每增加一个单位，y 的均值预计增加约0.069个单位。这个效应的大小是否具有实际意义，取决于 x 和 y 的单位以及它们所代表的实际量。例如，如果 y 是以百万美元计的利润，x 是广告投入（单位：万美元），那么 x 每增加一万美元，利润均值增加0.069百万美元（即6.9万美元），这可能被认为是实际显著的。但如果 y 是学生成绩（百分制），x 是学习时间（小时），那么学习时间每增加一小时，成绩均值增加0.069分，这个效应可能就太小了，不具有实际显著性。
    - 模型解释力 (Explanatory Power): R2=0.1227 (Multiple R-squared)，这意味着模型中的 x 解释了 y 总变异的约12.27%。这个解释比例相对较低，表明模型中还有大量未被 x 解释的 y 的变异。在某些领域，12%的解释力可能被认为有一定价值，但在其他领域可能被认为不足。
    - 结论: 要判断实际显著性，需要将这些统计结果（效应大小、模型解释力）放回具体的应用背景中进行评估。课件中的气泡备注也强调了这一点：“它是否足够大取决于上下文...是否足够大是主观的，并取决于单位。所以这里的重点是展示你理解这一点，而不是给出一个具体的数字或‘是/否’的答案。”
题目: 计算斜率的95%置信区间。
- 解析:
  - 斜率 β1 的95%置信区间可以使用公式：β^1±tα/2,n−p×SE(β^1)。
  - 从R输出中：β^1=0.06885，SE(β^1)=0.01308。
  - 自由度 df=n−p=198 (其中 n 是样本量，p 是参数个数，这里 p=2，包括截距和斜率)。
  - t0.025,198 的临界值。课件中使用了近似值1.97。我们可以用R精确计算：qt(0.975, df=198) 结果约为 1.9719。
  - 使用课件的1.97：
    - 下限: 0.06885−1.97×0.01308=0.06885−0.0257676=0.0430824≈0.0431
    - 上限: 0.06885+1.97×0.01308=0.06885+0.0257676=0.0946176≈0.0946
  - 所以，斜率的95%置信区间约为 (0.0431, 0.0946)。由于该区间不包含0，这也进一步证实了斜率是统计显著的。

判断题 (幻灯片 12)

题目: 在线性回归模型中，斜率的置信区间总是比截距的置信区间宽。
- 判断: 错误。
- 解析: 正如课件提示和之前的解析所述，置信区间的宽度取决于标准误。截距的标准误受 xˉ2 和样本量的影响，而斜率的标准误受 x 的散布程度 ∑(xi−xˉ)2 的影响。两者没有固定的宽度比较关系。例如，如果数据经过中心化处理使得 xˉ=0，截距的标准误会减小，其置信区间可能会比斜率的窄。
题目: 在一个简单线性回归模型中，均值的置信区间总是比使用零模型计算的置信区间宽。
- 判断: 错误。
- 解析: 此处“均值的置信区间”若指对特定 x0 处条件均值 E[Y∣x0] 的置信区间，其宽度与 x0 离 xˉ 的距离有关。当 x0=xˉ 时，该置信区间的宽度可能比零模型（仅估计总体均值 μY）的置信区间窄，特别是如果SLR的残差标准误 σ^ 小于零模型的残差标准误（通常如此）。如果 x0 远离 xˉ，则SLR的均值置信区间可能更宽。因此，该表述不总是成立。
题目: 对于两个不同置信水平的置信区间，较高置信水平的那个更宽。
- 判断: 正确。
- 解析: 为了以更高的置信度（如99% vs 95%）包含真实参数，置信区间需要覆盖更广的可能值范围，因此区间会更宽。这是因为较高置信水平对应于t分布或正态分布中更大的临界值。

多项选择题 (幻灯片 14)

题目: 假设 (1.93, 2.43) 是简单线性回归斜率 β1 的95%置信区间。以下哪个陈述是正确的？ A. 我们有95%的把握确信 β1 在1.93和2.43之间。 B. β1 在1.93和2.43之间的概率是95%。 C. β1 在1.93和2.43之间的概率是0.95。 D. 以上所有。 E. 以上皆非。

正确选项: A
解析:
- A 选项: 正确。这是对置信区间的标准频率学派解释。它表达了我们对这个具体计算出的区间能够包含真实、固定但未知的参数 β1 的信心程度。
- B 和 C 选项: 错误。在频率学派统计中，真实参数 β1 是一个固定的值，它没有概率分布。概率0.95是与构造区间的方法的长期可靠性相关的，而不是与这个特定的、已经计算出来的区间相关的。

来自 `2024_test_sol.pdf` (2024年春季测试题解析)

A部分：判断题 (Question 1)

(a) 题目 (3分): 在线性回归中，μi 的置信区间可能不包含 yi，但是 Yi=β0+β1xi+ϵi 的预测区间必须包含 yi，前提是 μi=E[Yi] 且 (xi,yi) 是用于构建线性模型的观测数据点。

判断: 错误 (✓ FALSE)
解析:
- μi=E[Yi∣xi] 是给定 xi 时 Y 的条件均值。其置信区间是针对这个均值的，而不是针对单个观测值 yi 的。因此，单个观测值 yi 完全可能落在其对应均值的置信区间之外，因为 yi=μi+ϵi，包含了随机误差 ϵi。
- 预测区间是针对一个新的、未观测到的 Y 值的。即使 (xi,yi) 是用于建模的观测数据点，我们为这个 xi 构造的预测区间是针对“如果再来一个具有相同 xi 的新观测 Ynew”的区间。这个区间同样因为包含未来观测的随机性，不保证必须包含原始的 yi。任何一个具体的 yi 都可能因为其特定的误差项 ϵi 而落在为其对应 xi 构建的预测区间之外。预测区间描述的是新观测值可能落入的范围，具有一定的概率（如95%），而不是对已观测数据点的必然包含。

(b) 题目 (3分): 以下R输出与给定的R命令一致。 ```R > predict(LM.fit, new.pred.df, interval = "predict") fit lwr upr 1 15.19726 12.87092 17.52360

> predict(LM.fit, new.pred.df, interval = "confidence")
fit      lwr      upr
1 15.19726  9.67879 20.71573
```

判断: 错误 (✓ FALSE)
解析:
- 对于相同的拟合值 (fit = 15.19726)，预测区间 (prediction interval) 总是比置信区间 (confidence interval) 更宽。这是因为预测区间不仅要考虑对均值估计的不确定性，还要考虑单个观测值围绕其均值的随机波动。
- 在给出的输出中，第一个命令是获取预测区间，其区间为 (12.87092, 17.52360)，宽度为 17.52360−12.87092=4.65268。
- 第二个命令是获取置信区间，其区间为 (9.67879, 20.71573)，宽度为 20.71573−9.67879=11.03694。
- 这里，预测区间的宽度 (4.65268) 小于置信区间的宽度 (11.03694)，这与理论相悖。因此，该R输出与给定的R命令不一致。

(c) 题目 (3分): 在线性回归中，假设 β1 是斜率，β^1 是对应的最大似然估计 (MLE)，那么即使简单线性回归模型的等方差假设不满足，E[β^1]=β1 仍然成立，前提是所有其他常规假设都满足。

判断: 正确 (✓ TRUE)
解析:
- 在线性回归模型中，最小二乘估计量 (OLS estimator) β^1（在高斯误差假设下也等同于最大似然估计量 MLE）的无偏性 (E[β^1]=β1) 依赖于以下核心假设：
  1. 模型线性于参数。
  2. 解释变量 X 是固定的（非随机的），或者与误差项 ϵ 无关 (E[Xϵ]=0)。
  3. 误差项的期望为零 (E[ϵi]=0)。
- 等方差假设 (homoscedasticity)，即 Var(ϵi)=σ2 对所有 i 都成立，主要影响的是 β^1 的方差表达式以及基于此方差的推断（如标准误、t检验、置信区间）的有效性和最优性（根据高斯-马尔可夫定理，OLS在同方差下是最佳线性无偏估计BLUE）。
- 如果仅仅是等方差假设不满足（即存在异方差），而其他假设（特别是 E[ϵi∣X]=0）仍然成立，那么 β^1 仍然是无偏的 (E[β^1]=β1) 和一致的。只是它不再是BLUE，其标准误的常规计算公式也不再准确。

B部分：多项选择题 (Question 2)

(a) 题目 (4分): 考虑一个对数-线性回归模型 log(yi)=β0+β1xi+ϵi，其中 ϵi∼Normal(0,σ2)，并且 β^1=1。假设 x 的值增加一个单位，那么以下哪个陈述是正确的？ *

☐ Yi 的期望对数值不会改变。 (The log of expected Yi would not change.)

☐ Yi 的期望对数值会增加1个单位。 (The log of expected Yi would increase by 1 unit.) 等价于log(EYi)但是要正确是得expect of log(Yi)即E(log(Yi))

☐ Yi 的期望对数值会增加2.7个单位。 (The log of expected Yi would increase by 2.7 unit.)

☐ Yi 的期望值会增加2.7个单位。 (The expected Yi would increase by 2.7 unit.)

☐ Yi 的期望值会增加170%。 (The expected Yi would increase by 170%.)

✓ 以上皆非。 (None of the above.)

正确选项: ✓ 以上皆非。
解析:
- 模型是 log(Yi)=β0+β1xi+ϵi。由于 ϵi∼Normal(0,σ2)，所以 log(Yi) 服从正态分布，其期望为 E[log(Yi)]=β0+β1xi。
- 当 xi 增加一个单位时，E[log(Yi)] 会增加 β1 个单位。题目中给出 β^1=1，所以 E[log(Yi)] 的估计值会增加1个单位。
  - 选项“Yi 的期望对数值不会改变”是错误的。
  - 选项“Yi 的期望对数值会增加1个单位”是正确的陈述，但需要注意这里说的是 E[log(Yi)] 而不是 log(E[Yi])。
- 对于原始尺度的 Yi，由于对数正态分布的性质，E[Yi]=E[eβ0+β1xi+ϵi]=eβ0+β1xiE[eϵi]=eβ0+β1xieσ2/2。
- 当 xi 增加一个单位到 xi+1 时，新的期望值 E[Ynew]=eβ0+β1(xi+1)eσ2/2。
- E[Ynew]/E[Yold]=eβ1。
- 如果 β^1=1，则 E[Yi] 的估计值会乘以 e1≈2.718。
- 这意味着 E[Yi] 的估计值会增加 (e1−1)×100。
- 选项“Yi 的期望值会增加2.7个单位”是错误的，因为是乘以约2.718，而不是增加2.7个单位（除非原期望为1）。
- 选项“Yi 的期望值会增加170%”接近正确答案171.8%，但题目通常要求精确。
- 关键点: 题目问的是“Yi 的期望对数值” (E[log(Yi)]) 还是“对数期望 Yi” (log(E[Yi]))。对于对数线性模型，我们通常解释的是 Yi 的中位数的变化，即中位数乘以 eβ1。如果假设 log(Yi) 的中位数等于其均值（因为正态分布对称），那么 Yi 的中位数会乘以 eβ1。
- 如果将“Yi 的期望对数值”理解为 E[log(Yi)]，那么它会增加 β1=1 个单位。
- 如果题目严格要求对 E[Yi] 的影响，那么是增加约171.8%。
- 由于选项中没有一个完全精确匹配 E[log(Yi)] 增加1单位，或者 E[Yi] 增加171.8%，或者中位数乘以 e1，所以选择“以上皆非”是最稳妥的。如果选项中有“Yi 的中位数会乘以约2.718倍”或“Yi 的中位数会增加约171.8%”，那将是更好的答案。
- 进一步辨析：在课程中，对于 log(Y)=β0+β1X+ϵ 模型，通常解释为 X 每增加一个单位，Y 的中位数乘以 eβ1。因为如果 log(Y) 服从正态分布，那么 Y 服从对数正态分布，其中位数是 eE[log(Y)]=eβ0+β1X。当 X 增加1时，中位数变为 eβ0+β1(X+1)=(eβ0+β1X)×eβ1。所以中位数乘以 e1≈2.718。这意味着中位数增加了约171.8%。
- 结论：选项中没有一个准确描述中位数的变化，也没有准确描述均值的变化。因此“以上皆非”是最佳答案。至少出现median才好说这东西有可能正确

C部分：简答题 (Question 3)

背景: 一个简单线性回归模型在R中拟合，输出摘要如下：

> summary(sim.fit) # 假设 sim.fit 是 lm(y ~ x) 的结果
Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max
-5.2822 -2.2645 -0.6545  1.7332  8.5444

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  8.72815    0.81354   10.73  2.15e-15 ***
x            1.96983    0.07611   25.88   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.07 on 58 degrees of freedom
Multiple R-squared:  0.9203,    Adjusted R-squared:  0.9189
F-statistic: 669.9 on 1 and 58 DF,  p-value: < 2.2e-16

(a) 题目 (1分): 数据框中有多少个数据点？

解析:
- 根据残差标准误 (Residual standard error) 那一行，自由度 (degrees of freedom) 是58。
- 对于简单线性回归模型 Y=β0+β1X+ϵ，有两个参数被估计 (β0 和 β1)。
- 残差自由度 dfresidual=n−p，其中 n 是数据点数量，p 是模型中参数的数量（包括截距）。
- 所以，58=n−2。
- 因此，n=58+2=60。
- 答案: 数据框中有60个数据点。

(b) 题目 (4分): 计算原假设 H0:β1=2 的t统计量。

解析:
- t统计量的计算公式为: T=SE(β^1)β^1−β1,0，其中 β1,0 是原假设中 β1 的值。
- 从R输出中可知：
  - 斜率的估计值 β^1=1.96983 (x的Estimate)。
  - 斜率的标准误 SE(β^1)=0.07611 (x的Std. Error)。
  - 原假设中 β1,0=2。
- 计算t统计量： T=0.076111.96983−2=0.07611−0.03017≈−0.3963999
- 答案: t统计量约为 -0.396。

(c) 题目 (4分): 在5%的显著性水平下，是否有证据反对 H0:β1=2？请说明理由。

解析:
- 判断: 没有足够的证据反对 H0:β1=2。
- 理由1 (基于t统计量):
  - 我们计算得到的t统计量 T≈−0.396。
  - 自由度为 df=58。
  - 对于双边检验，在5%的显著性水平下，我们需要比较 ∣T∣ 与 t0.025,58 的临界值。
  - qt(0.975, 58) 约等于 2.0017。
  - 因为 ∣−0.396∣=0.396<2.0017，所以t统计量的值没有落在拒绝域内。
  - 因此，我们不拒绝原假设 H0:β1=2。
- 理由2 (基于置信区间，如题目解析中所示):
  - 首先计算 β1 的95%置信区间：β^1±t0.025,58×SE(β^1)。
  - 1.96983±2.0017×0.07611=1.96983±0.15234
  - 置信区间为 (1.96983−0.15234,1.96983+0.15234)=(1.81749,2.12217)。
  - (题目解析中使用了近似的1.96作为t临界值，得到区间 (1.820654, 2.119006))。
  - 由于假设值 β1=2 包含在这个95%置信区间内（例如，2 在 (1.82, 2.12) 之间），我们没有足够的证据在5%的显著性水平下拒绝原假设 H0:β1=2。
- 答案: 没有足够的证据在5%的水平上反对 H0:β1=2，因为计算得到的t统计量绝对值远小于相应的t分布临界值，或者因为值2落在了斜率的95%置信区间内。

Question 4 (8分) - 药物滥用治疗效果研究

背景: 一项随机试验研究了对药物使用者进行住宿治疗的效果。大量受试者被随机分配接受3个月或6个月的治疗。其中，364人复吸。对于复吸的个体，研究者有兴趣估计每种治疗结束后到复吸的典型天数，以及两种治疗在复吸时间上的差异。数据框 drug.df 包含以下变量：

treat: 治疗分配 (Short 或 Long，分别对应3个月和6个月的治疗)
time: 治疗后到复吸的时间（天）

输出信息:

drug.df$treat 被转换为因子，水平为 "Short", "Long"。
原始 time 和 log(time) 按 treat 分组的箱线图和描述性统计。
- 原始 time 数据右偏明显。
- log(time) 数据看起来更对称，更接近正态。

对 log(time) 拟合线性模型 drug.loglm = lm(log(time) ~ treat, data=drug.df) 的系数摘要：

            Estimate Std. Error t value  Pr(>|t|)
(Intercept)   4.6823     0.06769   69.170 9.587e-211 ***
treatLong     0.2936     0.09763    3.007  2.819e-03 **

反转换后的置信区间 exp(confint(drug.loglm)):

               2.5%   97.5%
(Intercept)  94.559 123.404  (这是Short组复吸时间中位数的CI)
treatLong     1.107   1.625  (这是Long组相对于Short组复吸时间中位数的比率的CI)

(a) 题目 (1分): 为什么在分析前对复吸时间进行对数转换是合理的？

解析:
- 从提供的箱线图和描述性统计可以看出，原始的复吸时间 (time) 数据是高度右偏的 (例如，Short组均值162远大于中位数105)。对于右偏数据，中位数通常是比均值更好的典型值度量。
- 对数转换后 (log(time)) 的数据显示出更好的对称性，更接近正态分布的假设，这使得线性模型的假设（如误差正态性、方差齐性）更容易得到满足。
- 答案: 因为原始的复吸时间数据表现出明显的右偏性，对数转换有助于使数据分布更对称，更接近线性模型所要求的正态性假设，并且在这种情况下，模型结果（反转换后）通常解释为中位数效应，这对于偏态数据更为稳健和有意义。

(b) 题目 (4分): 写两句话（如同写执行摘要一样），一句量化短期和长期治疗在复吸天数上的差异，另一句量化短期治疗的复吸天数。

解析:
- 第一句 (差异): treatLong 的系数估计是0.2936，其指数 e0.2936≈1.341。置信区间为 (1.107, 1.625)。这意味着长期治疗组的复吸时间中位数是短期治疗组中位数的1.107到1.625倍。换算成百分比增加是 (1.107−1)×100 到 (1.625−1)×100。
  - 答案句1: 我们估计，接受长期（6个月）治疗的个体，其复吸时间的中位数比较短（3个月）治疗的个体高出10.7%到62.5%。
- 第二句 (短期治疗): 短期治疗是基准组 (treat="Short")，其复吸时间对数值的期望由截距估计。截距的估计值是4.6823。其反转换后的置信区间是 (94.559, 123.404)。
  - 答案句2: 对于接受短期治疗的个体，其复吸时间的中位数估计在95天到123天之间。
- (题目解析中给出的答案是：我们估计，长期（6个月）治疗的复吸时间中位数比短期（3个月）治疗高11%到63%。短期治疗的复吸时间中位数在95到123天之间。这与我们的计算基本一致。)

(c) 题目 (3分): 写出获取长期治疗后复吸时间置信区间的R命令。

解析:

长期治疗 (treat="Long") 不是基准组。我们需要为 treat="Long" 创建一个新的数据框，然后使用 predict() 函数在对数尺度上获得预测值和置信区间，最后进行指数反转换。

答案:

new.df <- data.frame(treat = factor("Long", levels = c("Short", "Long")))
# 或者如果 treat 已经是因子且 "Long" 是其一个水平: new.df <- data.frame(treat = "Long")
exp(predict(drug.loglm, newdata = new.df, interval = "confidence"))

或者使用 predictGLM (如果这是一个线性模型且 s20x 包已加载，但题目中是 lm):

# 如果 drug.loglm 是 lm 对象，predictGLM 可能不直接适用，除非 s20x 对其有封装
# 更标准的是手动计算或使用 predict.lm 的结果
# 以下是基于 predict.lm 的标准做法
pred_log_long <- predict(drug.loglm, newdata = data.frame(treat = "Long"), interval = "confidence")
exp(pred_log_long)

(题目解析中给出的R命令是正确的。)

来自 `test_sol(2).pdf` (2025年春季测试题解析 - 即今年的测试)

A部分：判断题 (Question 1)

(a) 题目 (3分): 在一个简单线性回归模型中，如果所有模型假设都满足且决定系数 R2 为0.9，那么响应变量Y和解释变量X必须有很强的线性关联。

判断: 正确 (✓ TRUE)
解析:
- 决定系数 R2 衡量的是解释变量 X 能够解释响应变量 Y 总变异的百分比。R2=0.9 意味着 X 解释了 Y 变异的90%。
- 在简单线性回归中，R2=(corr(X,Y))2，所以如果 R2=0.9，则相关系数 r=0.9≈±0.9487。
- 相关系数的绝对值接近1（如0.9487）表明 X 和 Y 之间存在非常强的线性关联。
- 前提是“所有模型假设都满足”，这确保了 R2 和相关系数的解释是有效的。

(b) 题目 (3分): 在线性回归中，summary输出中斜率的t检验的p值是斜率为零的概率。p-value是观测到极端数据的概率，概率越小说明越有可能成立，但是不能把p-value和某某某成立的概率绑定在一起

判断: 错误 (✓ FALSE)
解析:
- 这是一个对p值的常见误解。p值是在**原假设为真（即斜率为零）**的前提下，观察到当前样本数据（或更极端数据）的概率。
- 它不是“斜率为零的概率”。在频率学派统计中，总体参数（如真实的总体斜率）被认为是固定的未知常数，它没有概率分布，因此不能说它等于某个特定值的概率是多少。

(c) 题目 (3分): 在线性回归中，μi 的置信区间可能比 Yi=β0+β1xi+ϵi 的预测区间更宽，前提是所有常规假设都满足且 (xi,yi) 是用于构建线性模型的观测数据点。

判断: 错误 (✓ FALSE)
解析:
- μi=E[Yi∣xi] 是给定 xi 时 Y 的条件均值。其置信区间是针对这个均值的。
- Yi 的预测区间是针对一个新的、单个的观测值 Ynew（在给定的 xi 处）的。
- 预测区间总是等于或宽于对应 xi 处的均值置信区间。这是因为预测区间不仅包含了对均值估计的不确定性（这部分与均值置信区间相同），还额外包含了单个观测值围绕其均值的随机波动 ϵi 的不确定性。
- 因此，均值的置信区间不可能比预测区间更宽。

B部分：多项选择题 (Question 2)

(a) 题目 (4分): 考虑一个对数-对数线性模型 log(yi)=β0+β1log(xi)+ϵi，其中 ϵi∼Normal(0,σ2) 且 β^1=0.1。以下哪个陈述是正确的？

☐ Yi 的期望对数值如果 x 增加1个单位将不会改变。 (The log of expected Yi would not change if x was increased by 1 unit.)

☐ Yi 的期望对数值如果 x 增加1个单位将增加10%。 (The expected log of Yi would increase by 10% if x was increased by 1 unit.)

☐ Yi 的期望对数值如果 x 增加1个单位将增加0.1。 (The log of expected Yi would increase by 0.1 if x was increased by 1 unit.)

☐ Yi 的中位数如果 x 增加1%将增加10%。 (The median of Yi would increase by 10% if x was increased by 1%.)

☐ Yi 的对数中位数如果 x 增加1%将增加0.1%。 (The median of log of Yi would increase by 0.1% if x was increased by 1%.)

✓ 以上皆非。 (None of the above.)

正确选项: ✓ 以上皆非。
解析:
- 模型是 log(Yi)=β0+β1log(xi)+ϵi。
- 我们通常解释的是 xi 百分比变化对 Yi 中位数百分比变化的影响。
- 当 xi 增加1%时，Yi 的中位数大约增加 β1。题目中 β^1=0.1，所以当 xi 增加1%时，Yi 的中位数大约增加 0.1。
- 让我们逐个分析选项：
  - “Yi 的期望对数值如果 x 增加1个单位将不会改变。” 错误。这里 x 是绝对变化，且模型中是 log(x)。E[log(Yi)] 会改变。
  - “Yi 的期望对数值如果 x 增加1个单位将增加10%。” 错误。E[log(Yi)] 的变化是 β1×Δ(log(x))，不是简单的百分比。
  - “Yi 的期望对数值如果 x 增加1个单位将增加0.1。” 错误。E[log(Yi)] 的变化是 β1(log(x+1)−log(x))=0.1log((x+1)/x)，这不等于0.1。
  - “Yi 的中位数如果 x 增加1%将增加10%。” 错误。应该是增加约 0.1。
  - “Yi 的对数中位数如果 x 增加1%将增加0.1%。” 错误。Yi 的对数中位数是 E[log(Yi)]。当 x 增加1% (即 x 变为 1.01x) 时，log(x) 变为 log(1.01x)=log(1.01)+log(x)。所以 E[log(Yi)] 的变化是 β1log(1.01)=0.1×log(1.01)≈0.1×0.00995≈0.000995。这不是0.1%。
- 正确的陈述应该是：“Yi 的中位数如果 x 增加1%将大约增加 0.1。” 由于选项中没有这个陈述，所以选择“以上皆非”。

C部分：简答题 (Question 3)

背景: 一个二次回归模型 y∼x+I(x2) 在R中拟合，输出摘要如下：

> summary(lm(y ~ x + I(x^2)))
Call:
lm(formula = y ~ x + I(x^2))

Residuals:
    Min      1Q  Median      3Q     Max
-4.6231 -0.9615  0.0118  0.9832  3.9852

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  0.13947    0.05791   2.408 0.016200 *
x            0.14603    0.04736   3.083 0.002103 **
I(x^2)      -0.13152    0.03512  -3.744 0.000191 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.478 on 997 degrees of freedom
Multiple R-squared:  0.02245,   Adjusted R-squared:  0.02049
F-statistic: 11.45 on 2 and 997 DF,  p-value: 1.212e-05

(a) 题目 (1分): 数据框中有多少个数据点？

解析:
- 根据残差标准误 (Residual standard error) 那一行，自由度 (degrees of freedom) 是997。
- 模型是 Y=β0+β1X+β2X2+ϵ，有3个参数被估计 (β0,β1,β2)。
- 残差自由度 dfresidual=n−p，其中 n 是数据点数量，p 是模型中参数的数量。
- 所以，997=n−3。
- 因此，n=997+3=1000。
- 答案: 数据框中有1000个数据点。

(b) 题目 (5分): 计算 β2 (即 x2 的系数) 的95%置信区间。

解析:
- β2 的95%置信区间公式为：β^2±tα/2,n−p×SE(β^2)。
- 从R输出中可知：
  - x2 的系数估计值 β^2=−0.13152 (I(x^2)的Estimate)。
  - x2 的系数标准误 SE(β^2)=0.03512 (I(x^2)的Std. Error)。
  - 自由度 df=n−p=997。
- t0.025,997 的临界值。当自由度很大时（如大于100或200），t分布非常接近标准正态分布，所以可以使用 z0.025=1.96 作为近似。用R精确计算：qt(0.975, df=997) 结果约为 1.9623。题目解析中使用了1.96。
- 使用1.96：
  - 下限: −0.13152−1.96×0.03512=−0.13152−0.0688352=−0.2003552≈−0.20
  - 上限: −0.13152+1.96×0.03512=−0.13152+0.0688352=−0.0626848≈−0.06
- 所以，β2 的95%置信区间约为 (-0.20, -0.06)。
- 步骤评分点:
  - 1分: 知道公式 β^2±tα/2×SE(β^2)。
  - 1分: 正确读取 β^2=−0.13152。
  - 1分: 正确读取 SE(β^2)=0.03512。
  - 1分: 知道学生t分布可以被正态分布近似，因此 tα/2≈1.96。
  - 1分: 最终答案 (-0.20, -0.06)。

(c) 题目 (3分): 在5%的显著性水平下，是否有证据反对 H0:β2=−0.1？请说明理由。

解析:
- 判断: 没有足够的证据反对 H0:β2=−0.1。
- 理由 (基于置信区间):
  - 我们在 (b) 中计算出 β2 的95%置信区间约为 (-0.20, -0.06)。
  - 原假设的值 β2,0=−0.1。
  - 因为 −0.1 包含在置信区间 (−0.20,−0.06) 内 (即 −0.20<−0.1<−0.06)。
  - 当原假设的值落在参数的置信区间内时，我们没有足够的证据在相应的显著性水平下拒绝原假设。
- 步骤评分点:
  - 1分: 正确判断“没有证据”。
  - 1分: 知道使用置信区间与假设检验的对应关系。
  - 1分: 知道因为 −0.1∈(−0.20,−0.06)，所以在5%水平下没有证据反对。

Question 4 (8分) - FEV (用力呼气量) 研究

背景: 研究吸烟与用力呼气量 (FEV) 的关系。FEV是肺功能指标。数据来自654名3-19岁青少年。变量：

fev: FEV测量值。
ht: 身高 (英寸)。
smoke: 1为吸烟者，0为不吸烟者。

输出信息:

三个 trendscatter 图：fev~ht, log(fev)~ht, log(fev)~log(ht)。
三个模型的残差对拟合值图 (plot(fit, which=1))：
- fit1 = lm(fev ~ ht*smoke, ...)
- fit2 = lm(log(fev) ~ ht*smoke, ...) (对数线性模型)
- fit3 = lm(log(fev) ~ log(ht)*smoke, ...) (对数-对数模型)
三个模型的系数置信区间 (原始尺度和反转换后的百分比变化尺度)。

(a) 题目 (2分): 根据给定的输出，选择最佳模型。请说明理由。

解析:
- 选择: 对数线性模型 (fit2 = lm(log(fev) ~ ht*smoke, ...)) 似乎是最佳的。
- 理由:
  - 从趋势散点图来看：
    - fev~ht (左图) 显示出明显的曲线关系（向上弯曲）和异方差性（随身高增加，FEV的变异性增大）。这表明简单线性模型 fit1 可能不合适。
    - log(fev)~ht (中图) 使得关系看起来更接近线性，并且散点的垂直散布（方差）似乎更均匀。
    - log(fev)~log(ht) (右图) 也显示了线性关系，但与中图相比，其改善程度可能不那么明显，或者说中图的线性关系已经足够好。
  - 从残差图来看（虽然题目中只展示了 fit1 的一个残差图，但假设可以参考所有）：
    - fit1 (线性模型) 的残差图（题目中展示的第一个残差图）显示出明显的曲线模式（可能是U型或倒U型）和扇形散布（异方差），表明线性假设和等方差假设均不满足。
    - 根据题目解析的提示“对数线性模型在散点图和残差图中都略优于对数-对数模型”，我们可以推断 fit2 (对数线性模型) 的残差图表现最好，即残差随机分布在0附近，没有明显模式，且方差较为恒定。
    - fit3 (对数-对数模型) 的残差图可能也比 fit1 好，但可能不如 fit2。
- 答案: 对数线性模型 (fit2 = lm(log(fev) ~ ht*smoke, ...)) 似乎是最佳选择。理由是，原始的散点图和线性模型 (fit1) 的残差图都显示出曲线关系和拟合不足（或异方差）。而对数线性模型 (fit2) 的散点图（log(fev)~ht）和其对应的（未完全展示但可推断的）残差图表现出更好的线性关系和方差齐性，它在改善模型假设方面略优于对数-对数模型 (fit3)。

(b) 题目 (3分): 对于您选择的模型，写三句话（如同写执行摘要一样），第一句说明是否存在交互作用，第二句说明吸烟的影响，第三句量化身高的影响。

解析 (假设选择了 fit2 = lm(log(fev) ~ ht\*smoke, ...) 作为最佳模型):
- 我们需要查看 fit2 的 summary() 输出（题目未直接给出，但给出了其置信区间 confint(fit2)）。从 confint(fit2) 的输出中，ht:smoke 项的置信区间是 (-0.01409994, 0.009512541)。这个区间包含了0，表明交互作用项不显著。
- 如果交互作用不显著，我们通常会移除它并拟合主效应模型 lm(log(fev) ~ ht + smoke, ...)。但题目要求基于“你选择的模型”，而 fit2 是包含交互作用的。如果严格按 fit2 解释：
  - 第一句 (交互作用): FEV与身高之间的关系对于吸烟者和非吸烟者来说是相同的（或者说，没有足够的证据表明这种关系因吸烟状况而异，因为交互作用不显著）。
  - 第二句 (吸烟影响): 在控制了身高后，吸烟状况对FEV的中位数没有显著影响（因为 smoke 主效应的置信区间 (-0.63357410, 0.921653364) 对应的指数减1后包含0，表明OR的CI包含1）。
  - 第三句 (身高影响): 控制吸烟状况后，身高每增加一英寸，FEV的中位数预计增加5.1%到5.6%（来自 ht 项的置信区间 (0.05014065, 0.054451541)，反转换为百分比变化 100×(eCI−1)）。
- 更合理的做法 (如果允许模型简化): 由于交互作用不显著，应简化模型为 lm(log(fev) ~ ht + smoke, ...)。然后根据简化模型的 summary() 来解释 smoke 和 ht 的主效应。
  - 假设简化后 smoke 仍不显著，ht 显著。
  - 第一句 (交互作用): FEV与身高之间的关系对于吸烟者和非吸烟者来说是相同的。
  - 第二句 (吸烟影响): 在控制了身高后，我们没有发现吸烟状况对FEV有显著影响。
  - 第三句 (身高影响): 我们估计，身高每额外增加一英寸，FEV的中位数会增加X%到Y% (这里的X和Y来自简化模型后 ht 系数的置信区间并反转换)。
- 题目解析中给出的答案似乎是基于 fit1 (线性模型 fev ~ ht\*smoke) 或简化后的 fit2 (如果交互和smoke主效应都不显著，则简化为 log(fev) ~ ht)，并且混合了解释：
  - “用力呼气量和身高之间的关系对于吸烟者和非吸烟者是相同的。” (这暗示交互作用不显著)
  - “在给定的数据中，我们没有发现吸烟对用力呼气量有任何影响。” (这暗示吸烟主效应不显著)
  - “我们估计身高每额外增加一英寸，用力呼气量的均值会增加0.12到0.14个单位。” (这是对 fit1 中 ht 系数的解释，针对均值，且假设交互和吸烟都不显著)
  - “我们估计身高每额外增加一英寸，用力呼气量的中位数会增加5.1%到5.6%。” (这是对 fit2 中 ht 系数的解释，针对中位数，且假设交互和吸烟都不显著)
  - “我们估计身高每增加1%，用力呼气量的中位数会增加3.0%到3.3%。” (这是对 fit3 中 log(ht) 系数的解释)
- 选择最佳答案句 (基于题目解析倾向于简化模型后的解释):
  1. FEV与身高之间的关系对于吸烟者和非吸烟者是相同的。
  2. 在给定的数据中，我们没有发现吸烟对FEV的中位数有显著影响。
  3. 我们估计，身高每额外增加一英寸，FEV的中位数会增加5.1%到5.6%。 (选择与 fit2 对应的解释)

(c) 题目 (3分): 写下模型 fit3 的方程/公式，如同你在“方法与假设检查”部分所写的那样。

解析:
- fit3 是对数-对数模型，包含身高和吸烟状况的交互作用：lm(log(fev) ~ log(ht)*smoke, ...)。
- 模型方程可以写为： log(fevi)=β0+β1log(hti)+β2smokei+β3(log(hti)×smokei)+ϵi
- 其中：
  - fevi 是第 i 个个体的用力呼气量。
  - hti 是第 i 个个体的身高。
  - smokei 是一个指示变量，如果第 i 个个体吸烟则为1，否则为0。
  - ϵi∼iidNormal(0,σ2) 是误差项。
  - β0,β1,β2,β3 是固定但未知的模型参数。
- 步骤评分点:
  - 1分: 写出模型的基本形式 log(fevi)=⋯+ϵi。
  - 1分: 正确包含所有项，包括交互作用项 β3smokei⋅log(hti)，并说明误差项 ϵi∼Normal(0,σ2) 以及参数是固定但未知的。
  - 1分: 正确定义指示变量 smokei (例如，吸烟为1，不吸烟为0)。

代码总结

Lecture 1

这个lecture主要介绍了R语言在统计分析中的一些基本操作和概念，特别是围绕简单线性回归的初步探讨。

数据生成与描述:
- 使用 rnorm() 从正态分布中生成随机样本。
- 计算样本均值 (
```
mean()
```
  ,
```
sum()/length()
```
  ) 作为总体均值
```
true.mu
```
  的最大似然估计 (MLE)。这与教材
```
STATS201 book SWU 2023.pdf
```
  第1章介绍的通过R分析数据的概念一致。
单样本t检验:
- 使用 t.test(y, mu = value) 进行单样本t检验，用于检验总体均值是否等于某个特定值。代码中用 pi 是一个占位符，实际应为数值。
- 提及了估计、假设检验和置信区间都可以通过
```
t.test()
```
  函数获得，并强调了样本量对检验效能和置信区间宽度的影响。这部分内容与教材第3章“零线性模型与单样本t检验的等价性”相关。
相关性分析:
- 使用 plot(x,y) 绘制散点图来可视化两个变量之间的关系。
- 使用 cor(x,y) 计算皮尔逊相关系数，用以衡量线性关联的强度和方向。
- 通过实例（y的均值依赖于x，或y的标准差依赖于x的绝对值）强调了相关系数仅能捕捉线性关联，对于非线性关系（如异方差引起的扇形散点图），相关系数可能很低，即使变量间存在明显模式。

简单线性回归 (Simple Linear Regression):

引入 s20x 包，这是课程特定的包。
使用
```
data.frame()
```
创建数据框，这是R中存储表格数据的常用结构。对应教材第1章“将数据导入R - 创建数据框”部分。
使用
```
lm(y ~ x, data = data.df)
```
构建简单线性模型Y=β0+β1X+ϵ。这是本课程的核心内容之一，教材第1章“如何拟合直线到您的数据 - 简单线性模型”和第2章“简单线性回归的基础”详细讨论了这一点。

summary(fit)

  函数提供了模型系数的估计值、标准误、t统计量、p值以及模型的R2、F统计量等重要信息。教材第1章和第2章均有详细解释 。

- 手动计算 R2

   (

(TSS-RSS)/TSS

)，并与

summary(fit)

     中的结果对比。教材第1章“模型对预测有多好？ - R2”部分有讲解 。

5. **模型诊断 (Model Diagnostics)**:

   - `plot(fit, which = 1)` 生成残差对拟合值图，用于检查模型的**线性假设**和**方差齐性 (EOV)** 假设。
   - `normcheck(fit)` (来自`s20x`包) 或 `plot(fit, which = 2)` (标准R的Q-Q图) 用于检查残差的**正态性假设**。
   - `plot(fit, which = 4)` 生成Cook's距离图，用于识别**强影响点**。
   - 这些诊断方法是评估模型适用性的关键步骤，教材第2章“模型假设的标准检查 - 独立性、EOV和正态性”以及“使用cooks20x检查不当影响点”部分有详细说明 。

6. **模型解释与预测**:

   - `summary(fit)` 中的系数（斜率）解释。
   - `confint(fit)` 计算模型参数（截距和斜率）的置信区间（95%）。
   - `predict(fit, newdata = ..., interval = "confidence")` 计算给定新 x 值时，E[Y∣x] 的置信区间。
   - `predict(fit, newdata = ..., interval = "prediction")` 计算给定新 x 值时，单个 Y 值的预测区间。
   - 这些内容对应教材第1章“如何使用拟合模型进行预测”和第2章“置信区间和预测区间”。

7. **配对t检验的等价性**:

   - `t.test(x, y, paired = TRUE)` 执行配对t检验。
   - `t.test(x-y)` 对差值进行单样本t检验，其结果与配对t检验等价。
   - `summary(lm(x-y ~ 1, data = data.df))` 表明对差值拟合一个只有截距的模型（零模型），其截距的检验也与单样本t检验等价。这部分内容与教材第3章“零线性模型与单样本t检验的等价性”紧密相关 。

```R
# 真实参数未知但固定
true.mu = 3
# 从正态分布生成一个样本
y = rnorm(100, mean = true.mu, sd = 1)
# true.mu 的最大似然估计 (MLE)
mean(y)
sum(y) / length(y)
# 假设检验 H_0: mu_y = pi (这里的pi应理解为一个特定的常数值，例如3.14159...，但在t检验中通常用于表示总体均值假设值)
# 注意：实际代码中 t.test(y, mu = pi) 会引发错误，因为pi是内置常量。通常会用一个数值，如 t.test(y, mu = 3)
t.test(y, mu = pi) # 概念上是检验均值是否等于某个值，但pi的使用在此处不标准，除非pi被重新赋值

# 估计/假设检验/置信区间
# 上述函数 (t.test) 均可提供
# 注意检验的效能 (power)
# 以及置信区间的宽度
# 会随着样本量的改变而改变

# 生成两个独立的变量用于展示关系
y = rnorm(100, mean = 3, sd = 1)
x = rnorm(100, mean = 0, sd = 1)
plot(x,y) # 绘制散点图
# 皮尔逊相关系数
cor(x,y)
# 创建一些依赖关系
y = rnorm(100, mean = x, sd = 1) # y 的均值依赖于 x
plot(x,y)
cor(x,y)
# 注意相关性仅能
# 捕捉线性关联
x = rnorm(1000, mean = 0, sd = 1)
y = rnorm(1000, mean = 0, sd = abs(x)) # y 的标准差依赖于 x 的绝对值，创建了非线性关联 (异方差性)
plot(x,y)
cor(x,y) # 尽管存在明显模式，但线性相关系数可能接近0

library(s20x) # 本课程需要此包
y = rnorm(100, mean = 3, sd = 1)
x = rnorm(100, mean = 0, sd = 1)
data.df = data.frame(y=y,x=x) # 创建数据框
fit = lm(y~x, data = data.df) # 构建线性模型 y = beta0 + beta1*x
summary(fit) # 给出参数估计等信息
# R^2 (决定系数)
TSS = sum((y - mean(y))^2) # 总平方和 (Total Sum of Squares)
RSS = sum((y-fitted.values(fit))^2) # 残差平方和 (Residual Sum of Squares)
(TSS- RSS)/TSS # 计算 R^2，应与 summary(fit) 中的 R-squared 一致

# 残差图
plot(fit,which = 1) # 1. 残差 vs. 拟合值图，用于检查线性性和方差齐性 (EOV)
normcheck(fit) # 3. 正态性检验图 (通常是Q-Q图和残差直方图)
# plot(fit,which = 2) # 理论上 which=2 是 Q-Q plot，但 s20x 的 normcheck 更常用
plot(fit,which = 4) # 4. Cook's距离图，用于识别强影响点
# 如何解释斜率
summary(fit) # 回归系数的估计值、标准误、t值、p值
# 置信区间
confint(fit) # 参数的置信区间及其解释
# 预测区间
new.df = data.frame(x=pi) # 创建新的x值用于预测，同样pi的使用需注意
predict(fit, newdata = new.df, # 对给定x值的均值y的置信区间
        interval = "confidence")
predict(fit, newdata = new.df, # 对给定x值的单个y的预测区间
        interval = "prediction")

# t.test 中的参数
t.test(x,y,paired = TRUE) # 配对t检验
t.test(x-y) # 这等同于对差值进行单样本t检验 (检验差值的均值是否为0)
# 与零模型相同
summary(lm(x-y~1, data = data.df)) # 对差值拟合截距模型，其截距的t检验与单样本t检验等价

Lecture 2

这个lecture深入探讨了简单线性回归的基础 (The basics of simple linear regression)，重点在于理解模型参数的估计、推断（置信区间和预测区间）以及模型诊断。这与教材 STATS201 book SWU 2023.pdf 第2章的内容高度吻合。

参数估计与标准误:
- 首先通过模拟生成已知真实参数 (beta0, beta1, sd) 的数据。
- 使用 lm(y~x) 拟合模型。
- 手动从公式计算残差标准误 (
```
sigmahat
```
  ) 和斜率的标准误 (
```
sigma1hat
```
  )，并与
```
summary(fit)$sigma
```
  和
```
summary(fit)$coeff[2,2]
```
  的输出进行比较，帮助理解这些估计量是如何得到的。这对应教材第2章中关于最小二乘法拟合模型后，如何得到参数估计及其标准误差的讨论。
参数的置信区间:
- 手动计算斜率 beta1hat 的95%置信区间，使用公式 β^1±tα/2,n−p×SE(β^1)。
- 将其与
```
confint(fit)
```
  函数的结果进行比较，验证手动计算的正确性。这在教材第2章“参数和拟合值的置信区间，以及个体预测的预测区间”部分有详细描述。
- 通过模拟 (for循环) 展示了置信区间的覆盖率 (coverage probability) 概念：在多次重复抽样和构建置信区间的过程中，大约有95%的95%置信区间会包含真实的参数值。
预测区间与均值置信区间:
- 区分对条件均值 E[Y∣x] 的置信区间 (
```
interval = "confidence"
```
  ) 和对单个新观测值 Ynew 的预测区间
  
  (
```
interval = "prediction"
```
  )。教材第2章对此有详细解释。
- 预测区间总是比均值置信区间更宽，因为它额外考虑了单个观测的随机波动 ϵ。
- 通过模拟展示了预测区间的覆盖率，即大约95%的95%预测区间会包含真实的未来观测值。
拟合值与残差:
- fitted.values(simple.fit) 或 coef(simple.fit)[1] + coef(simple.fit)[2] * sim_data$x 用于获取拟合值 y^。
- sim_data$y - yhat 计算残差 e=y−y^。
- 这些概念是模型诊断的基础，教材第2章“拟合值和残差”部分有所提及。

模型诊断图:

plot(simple.fit, which = 1)

  ：残差对拟合值图，用于检查线性性和方差齐性 (EOV)。教材第2章“检查模型假设 - 独立性、EOV和正态性” 。

- `trendscatter(res ~ yhat)` (来自 `s20x` 包)：提供了另一种检查线性性和EOV的方法。

- ```
  normcheck(simple.fit)

 (来自 

s20x

 包)：用于检查残差的正态性。教材第2章 。

cooks20x(simple.fit)

(来自 

s20x

      包)：用于检查强影响点。教材第2章“使用cooks20x检查不当影响点” 。

   - 强调了样本量对诊断工具敏感性的影响：小样本时诊断图可能过于敏感。

6. **违反模型假设的情况**:

   - 模拟了违反方差齐性 (`sd = x`) 和违反残差正态性 (`error = error^2`) 的情况，并观察了这些违反对模型诊断图和回归线的影响。
   - 指出在违反EOV时，回归线可能仍接近真实情况，但违反正态性（特别是当它导致均值结构改变时）可能会使回归线偏离真实情况。

```r
# 真实且未知的参数
beta0 = 100
beta1 = 0.05
# 解释变量
x = 1:200
# 真实均值
mu = beta0 + beta1*x
# 响应变量 (带有随机误差)
y = rnorm(200, mean = mu, sd = 10)
# 构建模型
fit = lm(y~x)
summary(fit)
# 从公式计算估计的标准差 sigma_hat (残差标准误)
sqrt(sum((y - fitted.values(fit))^2)/(200-2)) # (n-p)，这里 p=2 (beta0, beta1)
# 从summary对象中提取估计的标准差 sigma_hat
sigmahat = summary(fit)$sigma
# 从公式计算斜率估计的标准误 sigma1_hat
sqrt(sigmahat^2/sum((x-mean(x))^2))
sigma1hat = summary(fit)$coeff[2,2] # summary(fit)$coefficients 是系数矩阵，[2,2]是斜率的标准误
# 提取斜率的估计值 beta1_hat
beta1hat = summary(fit)$coeff[2,1] # [2,1]是斜率的估计值
# 手动计算 beta1_hat 的95%置信区间下限和上限
beta1hat + qt(0.025, df = 198) * sigma1hat # df = n-p = 200-2 = 198
beta1hat + qt(0.975, df = 198) * sigma1hat
# 与R内置函数结果比较
confint(fit)

rm(list=ls()) # 清除工作空间中的所有对象
# 置信区间的覆盖率模拟
count = 0
N = 10000 # 模拟次数
for (i in 1:N){
  # 观测数量
  sample.size = 30
  # 预测变量
  x = 1:sample.size;
  # 真实截距和斜率
  beta0 = 5; beta1 = 2;
  # 真实误差项
  error = rnorm(n = sample.size, mean = 0, sd = 3)
  # 响应变量
  y = beta0 + beta1 * x + error;
  # 存入数据框
  sim_data = data.frame(x=x, y=y);
  # 拟合简单线性模型
  simple.fit = lm(formula = y~x, data = sim_data)
  # 获取斜率beta1的置信区间
  beta1.CI = confint(simple.fit)[2, ] # 提取斜率的置信区间
  # 如果真实beta1包含在计算得到的置信区间内，则计数
  count = count + as.numeric((beta1.CI[1] <= beta1) & (beta1<=beta1.CI[2]))
}
count / N # 计算覆盖率，应接近0.95

# 预测区间
new.df = data.frame(x = 7) # 给定新的x值
# 点预测值
predict(simple.fit, newdata = new.df, interval = "none") # 或者不指定 interval
# 对 E[y|x=7] = beta0 + beta1 * 7 的置信区间
predict(simple.fit, newdata = new.df, interval = "confidence")
# 对单个y (当x=7时) 的预测区间
predict(simple.fit, newdata = new.df, interval = "prediction")
# y的条件均值 (真实值)
beta0 + beta1 * 7
# 某个随机误差
(error = rnorm(n = 1, mean = 0, sd = 3))
# 某个真实的y值
beta0 + beta1 * 7 + error

# 95%预测区间的思想类似于95%置信区间
count = 0
N = 1000 # 模拟次数
sample.size = 30
x = 1:sample.size;
beta0 = 5; beta1 = 2;
new.df = data.frame(x = 7) # 新的x值
for (i in 1:N){
  error = rnorm(n = sample.size, mean = 0, sd = 3) # 生成样本误差
  y = beta0 + beta1 * x + error; # 生成样本y
  sim_data = data.frame(x=x, y=y);
  simple.fit = lm(formula = y~x, data = sim_data) # 拟合模型
  x7.PI = predict(simple.fit, newdata = new.df, interval = "prediction")[2:3] # 获取预测区间的下限和上限
  error = rnorm(n = 1, mean = 0, sd = 3) # 为新的观测值生成一个随机误差
  true.Y = beta0 + beta1 * 7 + error # 真实的新的Y值
  # 如果真实的Y值包含在预测区间内，则计数
  count = count + as.numeric((x7.PI[1] <= true.Y) & (true.Y<=x7.PI[2]))
}
count / N # 计算覆盖率，应接近0.95

rm(list=ls()) # 清除工作空间
library(s20x) # 加载s20x包
# 观测数量 20
sample.size = 20
# 预测变量
x = 1:sample.size;
# 真实截距 5 和斜率 2
beta0 = 5; beta1 = 2;
# 真实误差 Normal(0, sigma = 3)
error = rnorm(n = sample.size, mean = 0, sd = 3)
# 响应变量
y = beta0 + beta1 * x + error;
# 存入数据框
sim_data = data.frame(x=x, y=y);
# 拟合简单线性模型
simple.fit = lm(formula = y~x, data = sim_data)
# 提取估计的截距和斜率
coef(simple.fit)
# 拟合值，即给定x的条件y值，
# 其中x值是原始数据中观测到的
coef(simple.fit)[1] + coef(simple.fit)[2] * sim_data$x
# R中的内置函数
yhat = fitted.values(simple.fit)
# 残差
res = sim_data$y - yhat
# 将所有内容放入同一个数据框
sim_data$yhat = yhat
sim_data$res = res
head(sim_data) # 显示数据框前几行
# 绘制两个变量的散点图
plot(y~x, data = sim_data)
# 绘制估计的回归线
abline(coef(simple.fit), col = "red")
# 绘制真实的双变量关系线
abline(c(5, 2), col = "blue", lty = 2) # c(intercept, slope)
# 检查线性性和方差齐性 (EOV)
plot(simple.fit, which = 1)
# 更多用于线性性和EOV的可视化辅助
trendscatter(res ~ yhat) # s20x包的函数，残差对拟合值的趋势散点图
# 正态性检查
normcheck(simple.fit) # s20x包的函数
# 强影响点检查
cooks20x(simple.fit) # s20x包的函数

# 样本量 200
sample.size = 200
# 当样本量较小时，我们用于
# 线性性、EOV和正态性的诊断工具可能过于敏感 (假阳性)
# 当样本量足够大时，它们更可靠

# 违反EOV (方差齐性) 的情况
error = rnorm(n = sample.size, mean = 0, sd = x) # 误差标准差随x变化
# 非恒定的散点，Q-Q图也可能偏离
# 注意回归线仍然离真实情况不远
# eovcheck中的误差带是不正确的 (可能是指s20x包中eovcheck函数的特定行为)

# 违反正态性的情况
error = error^2 # 使误差项非正态 (卡方分布)
# 非恒定的散点，Q-Q图和直方图都表明有问题
# 回归线不再接近真实情况

Lecture 3：曲线拟合与分类解释变量 (Fitting Curves and Categorical Explanatory Variables)

这个lecture主要涵盖了两个重要主题：1) 使用线性模型拟合曲线关系，特别是二次多项式回归；2) 处理双水平分类解释变量。

拟合曲线关系 (Fitting Curves):
- 识别曲线关系
  
  ：通过散点图 (
```
plot()
```
  ,
```
trendscatter()
```
  ) 和简单线性回归的残差对拟合值图 (
```
plot(fit, which=1)
```
  ) 来识别数据中是否存在非线性（曲线）趋势。如果残差图显示出系统性模式（如U形或倒U形），则表明简单线性模型可能不适用。这部分对应教材
```
STATS201 book SWU 2023.pdf
```
  第4章“使用线性模型拟合曲线”的引言部分。
- 二次模型：当检测到曲线关系时，可以尝试添加解释变量的二次项 (如X2) 到模型中，即
  
  Y=β0+β1X+β2X2+ϵ。在R中，这通过
```
I(Assign^2)
```
  实现，
```
I()
```
  函数确保
```
^2
```
  按数学上的平方运算执行，而不是R公式中的特殊含义。教材第4章对此有详细讨论。
- 模型比较与可视化：比较简单线性模型和二次模型的残差图，看后者是否更好地消除了系统性模式。通过 lines() 和 predict() 函数在原始散点图上绘制两个模型的拟合线，直观比较拟合效果。
- 模型外推风险：强调了将模型用于解释变量范围之外的数据进行预测（外推）是非常危险的，因为模型的形式在数据范围之外可能完全不适用。

处理双水平分类解释变量 (2-level Categorical Explanatory Variable):

数据类型转换：分类数据在R中应为因子 (factor)

类型。如果原始数据是字符型，需要使用
```
as.factor()
```
进行转换。
```
str()
```
和
```
summary()
```
函数可以帮助查看和理解因子变量的结构和水平。这部分内容与教材第5章“具有2级分类（因子）解释变量的线性模型”的开始部分以及第1章中处理数据框的部分相关。
因子水平顺序：可以使用 factor(variable, levels = c("level_preferred_as_baseline", "other_level")) 来改变因子水平的顺序，这将影响 lm() 函数中选择哪个水平作为基准水平 (baseline level)。
可视化：对于一个数值响应变量和一个二元分类解释变量，plot(Y ~ X_factor) 会自动生成并排的箱线图 (boxplots)，这是比较两组分布的有效方式。summaryStats(Y, X_factor) (来自s20x包) 可提供按组的描述性统计。
模型拟合与解释：
- 可以直接在 lm() 中使用因子型解释变量，如 lm(Exam ~ Attend, data = Stats20x.df)。R会自动为因子变量创建指示变量 (indicator variables, or dummy variables)。如果因子有k个水平，通常会创建k-1个指示变量，其中一个水平作为基准。
- 对于双水平因子（如"No", "Yes"），如果"No"是基准，则模型是 E[Exam]=β0+β1×IAttend=Yes。β0是"No"组的均值Exam，β1是"Yes"组相对于"No"组的均值Exam的差异。教材第5章详细解释了这一点。
- 也可以手动创建数值指示变量 (0/1)，然后用其进行回归，结果是等价的，但这通常不如直接使用因子方便。
模型诊断：对于这类模型，线性性假设通常不是主要关注点（因为解释变量只有两个有效值）。但方差齐性 (EOV) 和残差的正态性仍然需要通过 plot(fit, which=1) 和 normcheck(fit) 进行检查。
置信区间与预测区间：predict() 函数可以用于获取各组的均值置信区间和个体预测区间。

rm(list=ls()) # 清除工作空间
library(s20x) # 加载s20x包
getwd() # 获取当前工作目录
# setwd() # 设置工作目录 (如果需要)
Stats20x.df = read.table( # 加载数据
  "STATS20x.txt", header = TRUE)
# 第一步是做探索性分析
plot(Exam~Assign, data = Stats20x.df) # Exam对Assign的散点图
# 有用的s20x绘图函数
trendscatter(Exam~Assign, data = Stats20x.df) # 带趋势线的散点图
# 第一个模型 (简单线性回归)
examassign.fit = lm(Exam~Assign, data = Stats20x.df)
# 检查线性性 + 方差齐性 (EOV)
plot(examassign.fit, which = 1)
# 有一些曲率的迹象
# 添加一个二次项
examassign.fit2 = lm(Exam~Assign+I(Assign^2), data = Stats20x.df) # I()确保^按数学运算处理
# 再次检查线性性 + EOV
plot(examassign.fit2, which = 1)
# 看起来好一些了
# 图片通常是模型的一个很好的展示
plot(Exam~Assign, data = Stats20x.df)
x = 0:20 # 用于评估 beta1_hat + beta2_hat * x 的x取值范围
lines(x, predict(examassign.fit,
                 data.frame(Assign=x)), col = "red") # 绘制简单线性模型拟合线
lines(x, predict(examassign.fit2,
                 data.frame(Assign=x)), col = "blue") # 绘制二次模型拟合线

# 理解模型在数据范围之外的行为
x = seq(-15, 25, by = 0.1) # 更宽的x取值范围
y = predict(examassign.fit2, data.frame(Assign=x)) # 使用二次模型预测
plot(y~x, type = "l", lty = 2) # 绘制整个预测曲线
lines(x[x>0 & x<20], y[x>0 & x<20], col = "blue") # 突出显示原始数据范围内的拟合
abline(v=range(Stats20x.df$Assign), lty = 2, col = "grey") # 标记原始数据x的范围
abline(h=c(0, 100), lty = 2, col = "grey") # 标记y的合理范围 (如考试分数0-100)
# 在数据范围之外使用模型总是存在风险的

rm(list=ls()) # 清除工作空间
library(s20x) # 加载s20x包
Stats20x.df = read.table(
  "STATS20x.txt", header = TRUE)
# 二元分类变量
head(Stats20x.df$Attend) # 查看Attend变量的前几行
# 字符型
summary(Stats20x.df$Attend) # 字符型变量的summary给出长度、类别、模式
# 将字符型转换为因子型
Stats20x.df$Attend = as.factor(
  Stats20x.df$Attend)
# 存储方式不同
str(Stats20x.df$Attend) # 查看因子型变量的结构，会显示levels
head(Stats20x.df$Attend)
summary(Stats20x.df$Attend) # 因子型变量的summary给出各level的频数
# 我们可以改变level的顺序
Stats20x.df$Attend = factor(
 Stats20x.df$Attend, level = c("Yes", "No")) # 将"Yes"设为第一个level (基准level会改变)
summary(Stats20x.df$Attend) # "Yes"在前，"No"在后
head(Stats20x.df$Attend)
# Summary已经能提供很多信息了
summaryStats(Stats20x.df$Exam,
             Stats20x.df$Attend) # s20x包函数，按Attend分组计算Exam的描述统计
# 绘图更直观
plot(Exam~Attend, data = Stats20x.df) # 自动生成箱线图
# Hack数据格式以便使用trendscatter
Stats20x.df$Attend2 = as.numeric(
  Stats20x.df$Attend == "Yes") # 创建数值型指示变量 (Yes=1, No通常为0，但这里取决于因子顺序)
# 上面代码取决于Attend的因子水平顺序。如果"Yes"是第一水平，则Yes为1，No为2。
# 如果要Yes=1, No=0，且原始因子水平是c("No", "Yes")，则应为 as.numeric(Stats20x.df$Attend == "Yes")
# 或者更稳妥的是: Stats20x.df$Attend2 = ifelse(Stats20x.df$Attend == "Yes", 1, 0)
with(Stats20x.df, table(Attend,Attend2)) # 交叉表验证转换
trendscatter(Exam~Attend2, data = Stats20x.df) # 使用数值化的Attend2绘图
# 简单地对关系建模
examattend2.fit = lm(Exam~Attend2, data = Stats20x.df) # 使用数值型指示变量建模
summary(examattend2.fit)
# 注意相似之处和不同之处
examattend.fit = lm(Exam~Attend, data = Stats20x.df) # 直接使用因子型变量建模
summary(examattend.fit) # R会自动处理因子变量的哑变量编码
# 在这种情况下不需要线性性检查 (因为解释变量只有两个点)
plot(examattend.fit, which = 1) # 残差图仍然可以看方差齐性
# EOV (方差齐性)
summaryStats(Stats20x.df$Exam, Stats20x.df$Attend) # 按组查看标准差
# 正态性
normcheck(examattend.fit)
# 强影响点
cooks20x(examattend.fit)
# 解释
coef(summary(examattend.fit)) # 系数解释
confint(examattend.fit) # 置信区间
# 在这种情况下，两种类型的CI密切相关
preds.df = data.frame(Attend = c("No", "Yes")) # 注意level顺序
predict(examattend.fit, preds.df, interval = "confidence") # 对均值的置信区间
predict(examattend.fit, preds.df, interval = "prediction") # 对个体的预测区间

Lecture 4：数据转换 (Data Transformations) - 特别是Log转换

这个lecture的核心是数据转换 (Data Transformations)，特别是对数转换 (log transformation) 在处理右偏数据、非线性关系以及解释模型时的应用。这与教材 STATS201 book SWU 2023.pdf 第6章“乘法线性模型 (Multiplicative linear models)” 紧密相关。

处理右偏数据与正态性:
- 许多现实世界的数据（尤其是涉及金额、计数的数据，如房价 Houses.df$price、理发花费 hair.df$hair）是右偏 (right-skewed) 的。
- 直接对这类数据拟合线性模型可能会违反正态性假设和方差齐性假设。
- 对数转换 log()通常可以使右偏数据更对称，更接近正态分布，从而满足线性模型的假设。如
```
lm(log(price)~1, data=Houses.df)
```
  后
```
normcheck()
```
  显示改善。教材第6章 (第13页) 展示了对数转换如何使房价数据更接近正态。
均值 vs. 中位数:
- 对于高度偏斜的数据，中位数 (median) 通常比均值 (mean) 更能代表数据的“典型”或中心趋势。
- 当对响应变量 Y 进行对数转换拟合模型 log(Y)=β0+β1X+ϵ 时，反转换 exp(β^0+β^1X) 得到的是 Y 的中位数估计，而不是均值估计。
- 因此，通过
```
exp(confint(LoggedPriceNull.fit))
```
  得到的置信区间是针对总体中位数的。教材第6章 (第14-17页) 详细解释了为何对数转换后的推断是关于中位数的。
- 代码中还演示了使用自助法 (bootstrap) 来估计均值的置信区间，并与基于CLT的confint(HousesNull.fit)结果比较。
处理非线性关系 (对数线性模型):
- 当响应变量与解释变量之间的关系不是直线，而是曲线（特别是指数增长或衰减型，如马自达汽车价格随车龄 price ~ age 的关系），对响应变量取对数 (log(price) ~ age) 可能使关系线性化。
- 这种模型 log(Y)=β0+β1X+ϵ 称为对数-线性模型 (log-linear model)。
- 拟合后，需要检查残差图 (
```
plot(LogPriceAge.fit, which = 1)
```
  ) 和正态性 (
```
normcheck(LogPriceAge.fit)
```
  ) 是否在新尺度上满足假设。教材第6章 (第35-37页) 展示了马自达数据的这个过程。
解释对数转换后的模型系数:
- 对于对数-线性模型
  
  log(Y)=β0+β1X:
  - β^1 表示当 X 改变一个单位时，log(Y) 的平均变化。
  - exp(β^1) 表示当 X 改变一个单位时，Y 的中位数的乘性因子。
  - (exp(β^1)−1)×100% 表示当 X 改变一个单位时，Y 的中位数的百分比变化。
- 代码中演示了如何计算和解释车龄每增加一年，马自达汽车价格中位数的百分比下降 (
```
100 * (exp(confint(LogPriceAge.fit)[2,])-1)
```
  )。教材第6章 (第44页) 有详细的解释。
- 对于多年变化，如5年折旧，可以通过 (exp(β^1))5
  
  或exp(5×β^1)来估计累积的乘性效应。教材第6章 (第47-49页)讨论了多年折旧。
对数转换与分类解释变量:
- 当解释变量是分类变量时（如性别 sex），对数转换同样适用。
- 模型 log(Y)=β0+β1Isex=male 中，exp(β^1) 表示男性相对于女性（基准组）Y 中位数的比率。
- (exp(β^1)−1)×100% 是男性相对于女性 Y 中位数的百分比差异。
- 代码中分析了理发花费 log(hair) 与性别 sex 的关系。

library(s20x) # 加载s20x包
Houses.df = read.table("AkldHousePrices.txt", header = TRUE) # 读取奥克兰房价数据
head(Houses.df$price) # 查看房价数据前几行 (单位：千美元)
# 正态性存疑
hist(Houses.df$price, breaks=20,main="",xlab="Price ($1000)") # 绘制房价直方图
abline(v = c(mean(Houses.df$price), median(Houses.df$price)),
       col = c("blue", "green"), lwd = 2) # 添加均值和中位数线
summary(Houses.df$price) # 房价的描述统计
HousesNull.fit=lm(price~1, data=Houses.df) # 拟合空模型 (仅截距)
normcheck(HousesNull.fit) # 对原始房价数据的残差进行正态性检验 (等同于对数据本身)
nrow(Houses.df) # 样本量是合理的 (94)
# 模拟样本均值 (自助法 Bootstrap)
# 注意：代码中 House.df$price 应该是 Houses.df$price (笔误)
bootstrappedMeanPrices = double(10000) # 初始化一个长度为10000的向量
for (i in 1:10000){
  tmp.vec = sample(Houses.df$price, # 此处修正了变量名
                   size = nrow(Houses.df),
                   replace = TRUE) # 有放回抽样
  y.bar = mean(tmp.vec) # 计算重抽样样本的均值
  bootstrappedMeanPrices[i] = y.bar
}
hist(bootstrappedMeanPrices) # 根据中心极限定理 (CLT)，样本均值的分布应接近正态
quantile(bootstrappedMeanPrices, c(.025, .975)) # Bootstrap置信区间
confint(HousesNull.fit) # 基于正态假设的均值置信区间 (与t检验结果一致)

# Log转换
LoggedPriceNull.fit=lm(log(price)~1, data=Houses.df) # 对log(price)拟合空模型
normcheck(LoggedPriceNull.fit) # 检查log(price)的正态性
confint(LoggedPriceNull.fit) # log尺度上均值(也是中位数)的置信区间
exp(confint(LoggedPriceNull.fit)) # 反转换回原始尺度，得到中位数的置信区间

Mazda.df = read.table("mazda.txt", header = T) # 读取马自达汽车数据
head(Mazda.df)
# 我们需要自己创建一个名为age的新变量
Mazda.df$age = 91 - Mazda.df$year # 数据收集于1991年
head(Mazda.df)
# 绘制数据散点图
trendscatter(price ~ age, data = Mazda.df) # s20x包函数，价格对车龄的趋势散点图
# 简单线性模型
PriceAge.fit = lm(price ~ age, data = Mazda.df)
plot(PriceAge.fit, which = 1) # 残差图，违反线性性假设
normcheck(PriceAge.fit) # 同时伴有正态性问题
# 尝试二次模型
PriceAge.quad.fit = lm(price ~ age+I(age^2), data = Mazda.df)
plot(PriceAge.quad.fit, which = 1) # 线性性可以了，但是...
normcheck(PriceAge.quad.fit) # 并没有解决正态性问题 (通常是异方差)
# 对price取log可以移除非线性趋势
trendscatter(price ~ age, data = Mazda.df) # 原始数据
trendscatter(log(price) ~ age, data = Mazda.df) # log(price) vs age
LogPriceAge.fit = lm(log(price) ~ age, data = Mazda.df) # 对数线性模型
plot(LogPriceAge.fit, which = 1) # 线性性和EOV看起来都不错了
normcheck(LogPriceAge.fit) # 正态性也可以了
cooks20x(LogPriceAge.fit) # 没有过分影响的点
summary(LogPriceAge.fit) # 现在如何解释斜率？

# 反转换 (Backtransform)
exp(confint(LogPriceAge.fit)) # 获取截距和斜率(的指数)的置信区间
# 反转换为百分比差异
100 * (exp(confint(LogPriceAge.fit)[2,])-1) # 对斜率的解释：车龄每增加1年，价格中位数变化的百分比
# 对斜率的解释: exp(beta1_hat) 是车龄增加1年时，价格中位数的乘性因子。
# (exp(beta1_hat) - 1) * 100% 是百分比变化。

# 5年内
# exp(confint(LogPriceAge.fit)[2,])^5 # 这是 (exp(beta1))^5 的置信区间，表示5年后的乘性因子
# 100 * (exp(confint(LogPriceAge.fit)[2,])^5 - 1) # 5年后价格中位数的总百分比变化
# 应该是 100 * (exp(5 * confint(LogPriceAge.fit)[2,]) - 1)
# 或者解释为：5年车龄的马自达汽车的中位数价格
# 预计比原始价值低52.76%到58.9%。(这里原文解释的是5年内的总折旧率)
# 更准确的说法: 5年车龄的马自达汽车的价值是新车价值的 exp(5*beta1_hat) 倍。
# 其置信区间是 exp(5 * lower_beta1) 到 exp(5 * upper_beta1)。
# 或者说，相比于车龄X的车，车龄X+5的车的价格中位数会变为原来的 exp(5*beta1) 倍。
# 所以这里原文的注释可能指 (exp(beta1_CI_lower))^5 和 (exp(beta1_CI_upper))^5
# 表示5年折旧的累积效应。
# 如教材P48所示，解释为 "the median price of Mazdas drops between 52.8% and 58.9% over 5 years"
# 计算方式是 100 * (exp(confint(LogPriceAge.fit)[2,])^5 - 1) 或 100 * (exp(5 * confint(LogPriceAge.fit)[2,]) -1)
# 后者更常见于直接解释5年总变化。前者是每年变化率的5次累积。
# 在教材P49， Case Study 6.1 中使用的是 exp(5 * confint(LogPriceAge.fit)[2,]) - 1
# 而代码中是 exp(confint(LogPriceAge.fit)[2,])^5 - 1。这两个在数值上可能略有差异但概念相似。

survey.df = read.table("survey.txt", header = TRUE, stringsAsFactors = T) # 读取调查数据
# 为了使事情稍微不那么混乱，我们将数据放入其自己的数据框中
hair.df = with(survey.df, data.frame(hair = hair, sex = sex)) # 提取理发花费和性别
plot(hair ~ sex, data = hair.df) # 理发花费对性别的箱线图
# 女性在理发上的花费似乎比男性多。
# 我们可以看到数据是相当右偏的。方差齐性似乎也有问题。
# 也许取对数会有帮助。
plot(log(hair) ~ sex, data = hair.df) # log(理发花费) 对 性别的箱线图
# 对数尺度/对数线性模型
hair.fit = lm(log(hair) ~ sex, data = hair.df)
plot(hair.fit, which = 1) # 残差图
normcheck(hair.fit) # 正态性检查
cooks20x(hair.fit) # 强影响点检查
summary(hair.fit)
# 将反转换后的输出列绑定在一起
cbind(exp(coef(hair.fit)), exp(confint(hair.fit))) # 估计值和置信区间 (中位数尺度)
100*(exp(confint(hair.fit)) - 1) # 百分比差异解释
pred.df = data.frame(sex = c("female", "male")) # 注意因子水平顺序
exp(predict(hair.fit, pred.df, interval = "confidence")) # 预测各性别理发花费中位数的置信区间

Lecture 5：幂律模型 (Power Law Models)

这个lecture主要讲解幂律模型 (Power law linear models)，通常通过对响应变量和解释变量都进行对数转换来实现。这与教材 STATS201 book SWU 2023.pdf 第7章“幂律线性模型” 的内容一致。

幂律关系:
- 当变量之间的关系被假设为 Y=αXβ1 形式时，称为幂律关系。这种关系在生物学（如体重与长度）、物理学等领域很常见。
- 对这个等式两边取对数，得到 log(Y)=log(α)+β1log(X)。令β0=log(α)，则模型变为log(Y)=β0+β1log(X)。这正是关于log(Y)和 log(X)的一个简单线性模型，也称为对数-对数模型 (log-log model)。教材第7章 (第9-10页) 推导了这个过程。
- 代码中以鲷鱼的重量 (wgt) 与长度 (len) 为例，展示了原始尺度上非线性的关系，而在双对数尺度上 (log(wgt) ~ log(len)) 呈现线性关系。
模型拟合与诊断:
- 使用 lm(log(wgt) ~ log(len), data=Snap.df) 拟合模型。
- 与简单线性回归一样，需要进行模型诊断：
  - plot(Snap.lm, which=1)：检查残差图的线性性和方差齐性。
  - normcheck(Snap.lm)：检查残差的正态性。
  - cooks20x(Snap.lm)：检查强影响点。
- 教材第7章 (第12-14页) 展示了这些诊断步骤。
模型解释:
- 在对数-对数模型log(Y)=β0+β1log(X)中，斜率β1有特殊的解释：
  - β1 表示 X 每改变1%，Y 的中位数大约改变 β1% (这是一个近似，仅在 β1 较小且百分比变化较小时较准确)。
  - 更精确地，如果 X 变为 kX（即 X 乘以因子 k），则 Y 的中位数变为 kβ1Ymedian。也就是说，Y 的中位数被乘以 kβ1。
  - 代码中演示了当长度增加1% (即 k=1.01) 时，重量中位数乘以 1.01β1。以及当长度增加50% (即 k=1.5) 时，重量中位数乘以 1.5β1。教材第7章 (第24-26页) 详细解释了这种解释方法。
预测:
- 在对数尺度上进行预测，然后使用 exp() 函数反转换回原始尺度，得到的是响应变量 Y 的中位数的点估计和区间估计。
- predict(Snap.lm, newdata, interval="confidence") 后取指数，得到的是给定 log(X) 时 E[log(Y)] (即 log(Median(Y))) 的置信区间。
- predict(Snap.lm, newdata, interval="prediction") 后取指数，得到的是给定 log(X) 时单个新 log(Y) 值的预测区间，反转换后是单个新 Y 值的预测区间（通常解释为中位数的预测）。
- 教材第7章 (第19页) 演示了如何预测30cm鲷鱼的重量中位数。
特定假设检验:
- 可以对斜率 β1 进行特定值的假设检验，例如，在生物学中，重量通常与长度的立方成正比（如果形状保持不变），这意味着在对数-对数模型中，β1 可能接近3。
- 代码中演示了如何手动计算t统计量和p值来检验H0:β1=3。这在教材第7章 (第20-21页) 也有提及。

总而言之，Lecture 5 介绍了如何通过双对数转换来处理幂律关系，将其转化为线性模型进行分析，并重点讲解了这种模型下系数的独特解释方式。

Snap.df=read.table("SnapWgt.txt",header=TRUE) # 读取鲷鱼(Snapper)重量数据
str(Snap.df) # 查看数据结构 (len: 长度, wgt: 重量)
plot(wgt~len, data = Snap.df) # 绘制重量对长度的散点图
plot(log(wgt)~log(len), # 绘制 log(重量) 对 log(长度) 的散点图
     data=Snap.df,
     xlab="log(Length)",
     ylab="log(Weight)")
Snap.lm=lm(log(wgt)~log(len),data=Snap.df) # 拟合对数-对数模型 (幂律模型)
plot(Snap.lm,which=1) # 残差对拟合值图，检查线性性和EOV
normcheck(Snap.lm) # 正态性检查
cooks20x(Snap.lm) # 强影响点检查
summary(Snap.lm) # 查看模型摘要
# 在对数尺度上绘图
plot(log(wgt)~log(len),
     data=Snap.df,
     xlab="log(Length)",
     ylab="log(Weight)")
abline(coef(Snap.lm),lty=5, col="red") # 添加拟合线
# 在原始尺度上绘图
plot(wgt~len, data = Snap.df)
pred.df = data.frame(len = 20:90) # 创建用于预测的长度序列
Snap.pred = exp(predict(Snap.lm, pred.df)) # 预测log(wgt)并反转换回wgt (中位数)
lines(pred.df$len, Snap.pred, col="red") # 在原始尺度图上添加拟合曲线
# 预测
Pred.df=data.frame(len=30) # 预测长度为30cm的鲷鱼
# 长度为30cm的鲷鱼的重量中位数
exp(predict(
  Snap.lm,Pred.df,
  interval="confidence")) # 对log(wgt)的均值(即log(中位数))进行区间估计，然后反转换
# 一条长度为30cm的鲷鱼的重量 (个体预测)
exp(predict(
  Snap.lm,Pred.df,
  interval="prediction")) # 对单个log(wgt)进行区间预测，然后反转换

# 重量和长度的关系是立方的吗？ (即检验 log(len) 的系数是否为3)
summary(Snap.lm) # 查看 log(len) 的系数估计值和标准误
confint(Snap.lm) # 查看 log(len) 系数的置信区间，看是否包含3
# 对应的p值是多少？(用于检验 H0: beta1 = 3)
beta1 = coef(Snap.lm)[2] # 提取 log(len) 的系数估计值
seBeta1 = summary(Snap.lm)$coefficients[2,2] # 提取 log(len) 系数的标准误
hyp = 3 # 假设的系数值
tstat = (beta1 - hyp)/seBeta1 # 计算t统计量
tstat
pval = 2 * (1 - pt( # 计算双边p值
  abs(tstat),
  df = nrow(Snap.df) - 2)) # df = n - p (p=2, 截距和斜率)
pval

# 如何解释beta1 (log(len)的系数)
confint(Snap.lm)[2,] # log(len)系数的置信区间
# 如果x增加1%，那么y的中位数大约增加beta1%。
# (1+0.01)^beta1_hat approx 1 + beta1_hat*0.01
# 所以y的中位数乘以 (1+0.01)^beta1_hat，即增加了 ((1+0.01)^beta1_hat - 1)*100%
1.01^confint(Snap.lm)[2,] # x增加1% (乘以1.01)，y的中位数乘以的因子范围
# 对于大的百分比变化不适用这种近似解释
# 如果x增加50% (乘以1.5)
1.5^confint(Snap.lm)[2,] # y的中位数乘以的因子范围
# (1.5^confint(Snap.lm)[2,] - 1) * 100% 是y的中位数增加的百分比范围

Lecture 6：包含数值和因子解释变量的线性模型 (Linear Models with Numeric and Factor Explanatory Variables) - 交互作用模型

这个lecture主要讨论了包含一个数值解释变量和一个因子（分类）解释变量的线性模型，特别是交互作用模型 (interaction model)。这与教材 STATS201 book SWU 2023.pdf 第8章“包含数值和因子解释变量的线性模型第1部分：交互作用模型” 的内容相对应。

交互作用的概念与可视化:
- 当一个数值解释变量（如 Test 分数）对响应变量（如 Exam 分数）的影响取决于另一个因子解释变量（如 Attend 是否出勤）的水平时，就存在交互作用。
- 通过绘制不同因子水平下的散点图和拟合线来可视化交互作用。例如，
```
plot(Exam ~ Test, pch = substr(Attend, 1, 1), col = ...)
```
  后，分别为
```
Attend="Yes"
```
  和
```
Attend="No"
```
  的学生群体绘制拟合的回归线。如果这两条线不平行，则暗示可能存在交互作用。教材第8章 (第4-9页)展示了类似的可视化。
构建交互作用模型:
- 在R的 lm() 函数中，交互作用可以通过 X1 * X2 的形式指定，这等价于 X1 + X2 + X1:X2。其中 X1 是数值变量，X2 是因子变量，X1:X2 是交互作用项。
- 模型形式为
  
  Y=β0+β1X1+β2IX2=level2+β3(X1×IX2=level2)+ϵ
  
  (以
```
X2
```
  为双水平因子为例)。
  - 对于基准水平 (如 Attend="No"，IAttend=Yes=0)：Y=β0+β1X1+ϵ。
  - 对于另一水平 (如 Attend="Yes"，IAttend=Yes=1)：Y=(β0+β2)+(β1+β3)X1+ϵ。
  - β3 代表了因子不同水平下，数值变量 X1 的斜率差异。如果 β3 显著不为零，则表明存在交互作用。
- 教材第8章 (第11-17页) 详细解释了模型的构建和参数含义。
模型诊断:
- 与之前的线性模型一样，需要检查残差图 (
```
plot(fit, which=1)
```
  for EOV and linearity for each group's fit), 正态性 (
```
normcheck(fit)
```
  ), 和强影响点 (
```
cooks20x(fit)
```
  ). 教材第8章 (第18-20页)也强调了这些步骤。

解释交互作用模型:

summary(fit) 会给出交互作用项 (Test:AttendYes) 的系数、标准误、t值和p值。
如果交互作用项显著 (p值较小)，则表明数值变量的效应确实因因子变量的水平而异。此时，不能孤立地解释主效应（如Test或Attend的系数），而应分别描述在因子各水平下数值变量的效应。
例如，对于Attend="No"的学生，Test每增加1分，Exam平均增加 β^Test 分。对于Attend="Yes"的学生，Test每增加1分，Exam平均增加 β^Test+β^Test:AttendYes 分。

confint(fit)

      可以给出所有参数（包括交互作用项）的置信区间。教材第8章 (第21-28页及32-35页) 提供了详细的解释和置信区间计算。

5. **不显著的交互作用 (Simpson's Paradox 类似情景)**:

   - 第二个例子（甲状腺重量 `thyroid` vs. 体重 `body` 和处理方式 `trt`）展示了一个重要情况：初始观察 `plot(thyroid ~ trt)` 可能显示因子效应，但在调整了数值协变量 (`body`) 后，并且考虑到交互作用不显著时 (`summary(thyroid.fit)` 显示 `body:trt` 不显著)，主效应模型 (`lm(thyroid ~ body + trt)`) 可能显示因子不再显著。
   - 这是因为因子不同水平间的响应差异可能完全由协变量的差异引起。例如，药物组的老鼠甲状腺较重，可能仅仅因为药物组的老鼠本身就比较重 (`plot(body ~ trt)` 显示药物组老鼠体重较大)。这种情况提示我们在解释因子效应时需要小心控制混淆变量。这部分内容实际上预示了第9章“不含交互作用的模型”的重要性。

总结来说，Lecture 6 教授了如何在包含数值和因子解释变量时考虑和建模它们之间的交互作用，如何解释这种模型，以及在解释时需注意潜在的混淆效应。

```r
library(s20x) # 加载s20x包
Stats20x.df = read.table("STATS20x.txt", header = T) # 读取数据
Stats20x.df$Attend = as.factor(Stats20x.df$Attend) # 将Attend转换为因子
plot(Exam ~ Test, data = Stats20x.df,
     pch = substr(Attend, 1, 1), cex = 0.7, # 点的形状根据Attend的第一个字母 ("Y"或"N")
     col = ifelse(Attend == "Yes", "blue", "red")) # 点的颜色根据Attend的值
# Test分数与Exam分数的散点图，
# 表明在每个出勤组（“Yes”或“No”）内，Test和Exam之间的正相关关系是合理线性的，
# 但两组的斜率可能不同。

## 模型构建和假设检查
examTestAttend.fit = lm(Exam ~ Test * Attend, data = Stats20x.df) # 构建带交互作用的模型
# Test * Attend 等价于 Test + Attend + Test:Attend
plot(examTestAttend.fit, which = 1) # 残差对拟合值图
normcheck(examTestAttend.fit) # 正态性检查
cooks20x(examTestAttend.fit) # 强影响点检查
summary(examTestAttend.fit) # 查看模型摘要
confint(examTestAttend.fit) # 查看系数的置信区间

## 可视化最终模型
predAttend.df = data.frame(Test = 1:21, Attend = "Yes") # 为"Yes"组创建预测数据
predSlackers.df = data.frame(Test = 1:21, Attend = "No") # 为"No"组创建预测数据
plot(Exam ~ Test, data = Stats20x.df,pch = substr(Attend, 1, 1), cex = 0.7,
     col = ifelse(Attend == "Yes", "blue", "red")) # 重新绘制原始散点图
lines(1:21, predict(examTestAttend.fit, predAttend.df), col = "blue", lty = 2) # 绘制"Yes"组的拟合线
lines(1:21, predict(examTestAttend.fit, predSlackers.df), col = "red", lty = 2) # 绘制"No"组的拟合线

thyroid.df = read.table("Thyroid.txt", header = TRUE) # 读取甲状腺数据
head(thyroid.df) # 查看数据前几行
str(thyroid.df) # 查看数据结构
# 为药物组vs对照组创建一个因子变量
thyroid.df$trt = with(
  thyroid.df, factor(
    ifelse(group == 1, "control", "drug"))) # group=1为对照组，否则为药物组
# 这似乎表明药物有用
plot(thyroid ~ trt, data = thyroid.df, xlab = "Treatment", ylab = "Thyroid weights") # 甲状腺重量对处理方式的箱线图
# 当以体重为条件时，效果不明显
plot(thyroid ~ body, type = "n", data = thyroid.df) # 空白散点图框架
text(thyroid.df$body, thyroid.df$thyroid, thyroid.df$group) # 用组别标签绘制点
# 我们应该调整体重差异
thyroid.fit = lm(thyroid ~ body * trt, data = thyroid.df) # 拟合带交互作用的模型
plot(thyroid.fit, which = 1) # 线性性和EOV似乎都还好
normcheck(thyroid.fit) # 正态性可能有问题，可能需要使用模拟
cooks20x(thyroid.fit) # 观测点12是否影响过大？
cooks.distance(thyroid.fit)[12] # 非常接近0.4的阈值
plot(thyroid ~ body, type = "n", data = thyroid.df) # 重新绘制框架
text(thyroid.df$body, thyroid.df$thyroid, 1:16) # 用观测序号绘制点，以识别影响点

# 模型构建和假设检查
summary(thyroid.fit) # 交互作用项不显著
thyroid.fit2 = lm(thyroid ~ body + trt, data = thyroid.df) # 拟合无交互作用（加性）模型
summary(thyroid.fit2) # 调整后的R平方证实了这一点
# 处理(trt)似乎不显著
thyroid.fit3 = lm(thyroid ~ body, data = thyroid.df) # 仅用body拟合模型
summary(thyroid.fit3)
# 为什么`trt`不显著？
plot(body ~ trt, data = thyroid.df, main = "", xlab = "Treatment", ylab = "Mouse weight") # 小鼠体重对处理方式的箱线图
# 图中的差异是由于较重的小鼠甲状腺较重，
# 而药物组的小鼠较重。

Lecture 7

这个lecture继续探讨包含一个数值变量 (IQ) 和一个因子变量 (method) 的线性模型，重点关注当交互作用不显著时的模型简化和解释。这直接对应教材 STATS201 book SWU 2023.pdf 第9章“包含数值和因子解释变量的线性模型第2部分：不含交互作用的模型”。

从交互作用模型到主效应模型:
- 首先，如Lecture 6所示，拟合一个包含交互作用的模型 (
```
lm(lang ~ IQ * method, data = teach.df)
```
  )。
- 使用
```
anova(teach.fit)
```
  来检验交互作用项的显著性。如果交互作用不显著 (P值较大)，则根据奥卡姆剃刀原则 (Occam's Razor)或KISS原则 (Keep It Simple, Statistician)，应移除交互作用项，简化模型。教材第9章 (第14-18页) 详细讨论了模型选择和奥卡姆剃刀。
- 简化后的模型称为主效应模型或加性模型，形式为
```
lm(lang ~ IQ + method, data = teach.df)
```
  。在这个模型中，数值变量 (
```
IQ
```
  ) 的效应（斜率）对于因子变量 (
```
method
```
  ) 的所有水平都是相同的，但因子变量的不同水平有不同的截距。在图形上表现为一组平行线。

解释主效应模型:

summary(teach.fit2)

会给出主效应模型中 

IQ

的系数 (共同斜率) 和 

method

   各水平相对于基准水平的截距差异。 

- 例如，如果基准是 

method1

     ，模型为E[lang]=β0+β1IQ+β2Imethod=2+β3Imethod=3。

     - β1 是IQ对语言分数的共同效应。
     - β0 是 `method1` 组在IQ为0时的期望语言分数 (通常IQ为0无实际意义，所以截距的绝对值解释需谨慎，但差异是有意义的)。
     - β2 是 `method2` 组相对于 `method1` 组的平均语言分数差异 (控制IQ后)。
     - β3 是 `method3` 组相对于 `method1` 组的平均语言分数差异 (控制IQ后)。

   - 教材第9章 (第21页) 描述了这种模型的公式和参数解释。

3. **更改基准水平 (Releveling)**:

   - `summary()` 和 `confint()` 的输出是相对于当前基准水平的。为了得到所有因子水平之间的两两比较的置信区间（例如，`method2` vs `method3`），需要更改基准水平并重新拟合模型。

   - 使用 

relevel(factor_variable, ref = "new_baseline_level")

来更改基准。例如，

teach.df$method = relevel(teach.df$method, ref = "2")

将 

method2

      设为新的基准。 

   - 通过这种方式，可以获得所有配对比较的估计和置信区间。教材第9章 (第28-31页) 演示了如何更改基准水平并解释结果。

4. **比较包含与不包含协变量的模型**:

   - 代码中还比较了包含协变量 `IQ` 的模型 (`teach.fit2`) 和不包含 `IQ`、仅有 `method` 的模型 (`teach.fit5`，即单因素方差分析模型)。
   - 通过比较 R2 或调整后的 R2 (`summary(model)$r.squared`, `summary(model)$adj.r.squared`)，可以看出加入协变量 `IQ` 后模型解释变异的百分比是否提高。
   - 通常，如果协变量与响应变量相关，调整它会使得对因子效应的估计更精确（标准误更小），置信区间更窄。

5. **模型诊断**:

   - 对于最终选择的主效应模型，仍需进行标准的模型诊断，如检查残差图 (`plot(teach.fit2, which = 1)`), 正态性 (`normcheck(teach.fit2)`), 和强影响点 (`cooks20x(teach.fit2)`).

总结：Lecture 7 侧重于在多解释变量（一个数值，一个因子）模型中，当交互作用不显著时，如何简化到主效应模型，并如何通过更改因子基准水平来全面解释因子各水平间的差异。同时，也展示了控制协变量的重要性。

```r
library(s20x) # 加载s20x包
data(teach.df) # 加载s20x包中的teach.df数据集 (教学方法、IQ对语言分数的影响)
head(teach.df) # 查看数据前几行
str(teach.df) # 查看数据结构
# 我们需要将method转换为因子变量
teach.df$method = factor(teach.df$method)
plot(lang ~ IQ, main = "Language Score versus IQ (by method)", # 语言分数对IQ的散点图，按教学方法分组
     pch = as.character(teach.df$method), data = teach.df) # 点的形状根据方法 (1,2,3)
# 看起来有三条平行线。
# 分数随着IQ的增加而增加，方法2的
#得分最高，方法3得分最低。
# 这些单独线条周围的变异性远低于
# 在分开的图中看到的变异性。
# 这里有方差分析 (Anova) 的思想!!!
teach.fit = lm(lang ~ IQ * method, data = teach.df) # 拟合带交互作用的模型
plot(teach.fit, which = 1) # 残差对拟合值图
normcheck(teach.fit) # 正态性检查
cooks20x(teach.fit) # 强影响点检查
anova(teach.fit) # 方差分析表，用于检验交互作用的显著性
teach.fit2 = lm(lang ~ IQ + method, data = teach.df) # 拟合无交互作用 (加性/主效应) 模型
plot(teach.fit2, which = 1) # 新模型的残差图
normcheck(teach.fit2) # 新模型的正态性检查
cooks20x(teach.fit2) # 新模型的强影响点检查
anova(teach.fit2) # 新模型的方差分析表
summary(teach.fit2) # 查看模型摘要
confint(teach.fit2) # 系数的置信区间
# 无交互作用但截距不同
plot(lang ~ IQ, main = "Language Score versus IQ (by method)",
     pch = as.character(teach.df$method), data = teach.df) # 重新绘制散点图
abline(teach.fit2$coef[1], teach.fit2$coef[2], lty = 1) # 为基准方法绘制拟合线 (平行线)
abline(teach.fit2$coef[1] + teach.fit2$coef[3], teach.fit2$coef[2], lty = 2) # 为第二个方法绘制拟合线
abline(teach.fit2$coef[1] + teach.fit2$coef[4], teach.fit2$coef[2], lty = 4) # 为第三个方法绘制拟合线
# 更改基准水平以获得方法1的置信区间 (相对于方法2)
teach.df$method = relevel(teach.df$method, ref = "2") # 将方法2设为基准
teach.fit3 = lm(lang ~ IQ + method, data = teach.df) # 重新拟合模型
# 为什么查看这些模型的截距是有意义的
confint(teach.fit2) # 原基准 (方法1) 下的置信区间
confint(teach.fit3) # 新基准 (方法2) 下的置信区间 (可以得到方法1和方法3相对于方法2的比较)
# 如果不调整IQ会发生什么？(即只用method作为解释变量 - 单因素方差分析)
teach.fit4 = lm(lang ~ method, data = teach.df) # 注意，此时method的基准是"2"
teach.df$method = relevel(teach.df$method, ref = "1") # 将基准改回方法1
teach.fit5 = lm(lang ~ method, data = teach.df)
teach.df$method = relevel(teach.df$method, ref = "3") # 将基准改为方法3
teach.fit6 = lm(lang ~ method, data = teach.df)
confint(teach.fit5) # 仅包含method时，各水平与方法1的比较
confint(teach.fit6) # 仅包含method时，各水平与方法3的比较
summary(teach.fit2)$r.squared # 包含IQ和method的模型的R方
summary(teach.fit5)$r.squared # 仅包含method的模型的R方 (比较R方大小)

summary(teach.fit2)$adj.r.squared # 调整后的R方
summary(teach.fit5)$adj.r.squared # 调整后的R方

Lecture 8：多重线性回归与共线性问题 (Multiple Linear Regression and Multicollinearity)

这个lecture主要涉及多重线性回归 (Multiple Linear Regression)，即模型中包含多个解释变量（可以是数值型或因子型），并初步探讨了多重共线性 (Multicollinearity) 问题。这与教材 STATS201 book SWU 2023.pdf 第10章 “多重线性回归模型” 的内容一致。代码后半部分还涉及了单因素方差分析 (One-way ANOVA) 和 emmeans 包的使用，这与第11章内容相关。

这个lecture主要涵盖多重线性回归 (Multiple Linear Regression) 的模型构建策略、多重共线性 (Multicollinearity) 问题，以及单因素方差分析 (One-way ANOVA) 中的多重比较 (Multiple Comparisons) 问题。

多重线性回归与模型构建策略 (婴儿出生体重案例):
- 初始模型与变量筛选
  
  ：当有多个潜在解释变量时，一种策略是先拟合一个包含所有变量的“完整模型” (
```
lm(bwt ~ ., data = Babies.df)
```
  )，然后逐步剔除不显著的变量。但这种方法可能因多重共线性而出问题。
- 创建新变量
  
  ：有时需要根据理论或数据洞察创建新的解释变量，如从母亲的
```
weight
```
  和
```
height
```
  计算出
```
bmi
```
  。
- 探索性数据分析 (EDA)
  
  ：在构建复杂模型前，使用
```
pairs20x()
```
  (或标准
```
pairs()
```
  ) 和单独的散点图 (
```
plot()
```
  ,
```
lowess()
```
  ) 来检查变量间的关系、识别非线性、异常值和潜在的交互作用。
- 处理特殊关系：婴儿出生体重与孕龄(gestation)的关系呈现“曲棍球棒”形状（先增加后平缓或略降）。代码通过创建一个指示变量 OD (是否逾期，以294天为界) 并拟合交互作用模型 lm(bwt ~ gestation * OD, ...) 来尝试捕捉这种分段线性关系。这在教材第10章 (第17-21页) 有案例说明。
- 逐步回归思想：代码中通过一系列模型 (bwt.fit 到 bwt.fit9) 展示了逐步添加变量并检查其显著性的过程，这是一种模型选择的方法。移除异常影响点 (Babies.df[-c(239, 820), ]) 也是模型构建的重要一步。教材第10章 (第22-43页) 详细演示了婴儿出生体重数据的逐步建模过程。
- 模型诊断
  
  ：对最终选择的模型 (
```
bwt.fit9
```
  ) 进行了残差图、正态性和影响点检查。
多重共线性 (Multicollinearity):
- 当模型中包含高度相关的解释变量时（如同时包含
```
weight
```
  、
```
height
```
  和由它们计算出的
```
bmi
```
  ），会导致参数估计的标准误增大，使得原本可能显著的变量变得不显著。这就是多重共线性问题。
- 代码中 bwt.fit6 的 summary 显示 weight, height, bmi 可能都不显著，而 bwt.fit7 (移除了weight) 中 height 和 bmi 变得显著。这是共线性的一个典型表现。教材第10章 (第38-41页) 讨论了这个问题。
- 解决方法通常是移除导致共线性的变量之一，或使用其他降维技术（本课程未深入）。

单因素方差分析 (One-way ANOVA) (果蝇寿命案例):

当解释变量是一个有多于两个水平的因子时 (如 group)，我们实际上是在进行单因素方差分析。
lm(days ~ group, data = Fruitfly.df) 拟合模型。

anova(ff.fit)

给出总的F检验，判断因子 

group

是否显著影响响应变量 

days

     。 

   - `summary(ff.fit)` 显示各因子水平与基准水平的差异。

   - 这部分内容与教材第11章 “具有单个多于两个水平的因子解释变量的线性模型（单因素方差分析）” 相关。

4. **多重比较问题与 `emmeans` (果蝇寿命案例)**:

   - 当一个因子有多个水平，并且我们想比较所有水平两两之间的均值差异时，会遇到多重比较问题：进行多次假设检验会增加至少犯一次第一类错误（错误地拒绝真实的原假设）的概率。 

   - 模拟代码部分（`for (i in 1:1000){...}`) 试图通过模拟演示在原假设为真（即所有组均值相同）的情况下，随机选择的两个组（特别是均值差异最大的两个组）进行比较时，仍有可能观察到“显著”差异的现象，这突显了多重比较校正的必要性。第二个模拟（关于二次模型参数的置信区间覆盖率）说明了单个参数CI的覆盖率约为95%，但所有参数同时被其CI覆盖的概率会更低。

   - `emmeans` 包 (`library(emmeans)`) 提供了进行多重比较校正的工具。

   - `emmeans(ff.fit, ~group)` 计算各组的估计边际均值。

   - ```
     pairs(emmeans_object, infer=TRUE)

 进行所有两两比较，并默认使用Tukey方法调整p值和置信区间，以控制总体错误率。

教材第11章 (第18-24页) 详细介绍了多重比较问题和使用 emmeans 进行Tukey调整的方法。

总结：Lecture 8 覆盖了多重回归中的实际建模步骤、共线性这一重要问题，并引入了 ANOVA 后进行多重比较的概念和工具，这些都是统计建模中非常核心和实用的技能。

library(s20x) # 加载s20x包
Babies.df = read.table("babies_data.txt", header = T) # 读取婴儿出生体重数据
# 拟合完整模型 (包含所有变量)
bwt.all.fit = lm(bwt ~ ., data = Babies.df) # "."代表数据框中除响应变量外的所有其他变量
summary(bwt.all.fit)
bwt.no.age.fit = lm(bwt ~ .-age, data = Babies.df) # 从模型中移除age变量
summary(bwt.no.age.fit)
# 母亲体重过轻或严重超重
# 会对婴儿健康产生负面影响，
# 但身高或体重都不能直接衡量这一点。
# 让我们从这两个测量值创建BMI (身体质量指数)
Babies.df$bmi = with(Babies.df, weight/(height^2) * 703) # 注意单位转换因子703 (磅/英寸^2)
# 重新拟合新的完整模型 (包含BMI)
bwt.all.fit = lm(bwt ~ ., data = Babies.df) # 再次拟合所有变量，现在包括了bmi
summary(bwt.all.fit)
bwt.no.age.fit = lm(bwt ~ .-age, data = Babies.df) # 再次移除age
summary(bwt.no.age.fit)
# 多重共线性 (当解释变量高度相关时出现的问题)
# 比从完整模型开始更好的方法
# 进行一些探索性分析
pairs20x(Babies.df[, c(1, 2, 4, 5, 6)]) # 绘制数值变量间的成对关系图 (bwt, gestation, age, height, weight)
# 查看成对关系图，
# 我们发现`bwt`与母亲的`height`和`weight`之间关系较弱。
# 婴儿的孕龄(`gestation`)与其出生体重`bwt`之间有更强的关系，
# 这不足为奇，因为孩子在母亲子宫里的时间越长，
# 孩子就有越多的时间获得营养并成长——直到某个点，
# 然后关系某种程度上“变平”。42周 = 42 * 7 = 294天。
# 母亲的`age`与其孩子的`bwt`之间似乎没有任何关系。
# 让我们更深入地研究`bwt`和`gestation`之间的关系。
plot(bwt ~ gestation, data = Babies.df, col = "gray60") # bwt对gestation的散点图
lines(lowess(Babies.df$gestation,Babies.df$bwt), col = "tomato", lwd = 2) # 添加loess平滑曲线
text(152, 120, "?") # 标记可能的异常点
text(185, 115, "?") # 标记可能的异常点
abline(v = 294, col = "steelblue", lwd = 2) # 在294天处画一条垂直线 (孕期转折点)
# 注意，这些图中似乎也有一些“奇怪”的数据点。
which(Babies.df$gestation<200) # 找出孕期小于200天的观测
# 分类(因子)数据变量与婴儿出生体重(`bwt`)之间关系不大。
pairs20x(Babies.df[, c(1, 3, 7)]) # bwt, not.first.born, smokes

# 像之前提到的那样创建OD (Overdue Days，是否逾期)
Babies.df$OD = as.numeric((Babies.df$gestation > 294)) # 如果gestation > 294则为1，否则为0
range(Babies.df$gestation[Babies.df$OD == 0]) # 检查OD=0时的孕期范围
range(Babies.df$gestation[Babies.df$OD == 1]) # 检查OD=1时的孕期范围
bwt.fit = lm(bwt ~ gestation * OD, data = Babies.df) # 拟合孕龄和是否逾期的交互作用模型 (分段线性)
plot(bwt.fit, which = 1) # 线性性和EOV检查
normcheck(bwt.fit) # 正态性检查
cooks20x(bwt.fit) # 影响点检查 (此时会发现239, 820号点影响大)
bwt.fit2 = lm(bwt ~ gestation * OD, data = Babies.df[-239, ]) # 移除239号点后重新拟合
cooks20x(bwt.fit2) # 再次检查影响点 (此时会发现原820号点，现819号点影响大)
bwt.fit3 = lm(bwt ~ gestation * OD, data = Babies.df[-c(239, 820), ]) # 移除239和820号点后重新拟合
cooks20x(bwt.fit3) # 最终影响点检查
summary(bwt.fit3) # 交互作用是显著的

gestation.seq=201:360 # 用于预测的孕期序列
ODdays.seq=ifelse(gestation.seq<=294,0,1) # 对应的OD序列 (注意：这里应该是OD，而不是ODdays)
# 代码中ODdays.seq的定义与前面OD的0/1定义一致，用于指示是否进入第二段。
# 但模型bwt.fit3是用 gestation*OD 拟合的。如果想实现分段斜率，
# 需要创建类似 gestation_after_294 = ifelse(gestation > 294, gestation - 294, 0) 的变量。
# 或者如教材P20所示的 (gestation-294)*OD。
# 当前的 gestation*OD 会产生不同的截距和斜率，但不是典型的分段点斜率突变模型。
# 假设这里的目的是可视化两个不同阶段的线性关系（如果OD是0或1）
fit.seq=predict(bwt.fit3,new=data.frame(gestation=gestation.seq, OD=ODdays.seq))
plot(bwt~gestation,data=Babies.df[-c(239, 820),],ylab="Birth weight (oz)") # 修正笔误，使用清洗后的数据绘图
lines(gestation.seq,fit.seq,col="red"); abline(v=294,lty=2,col="blue")

# 当前模型是什么？逐步添加变量
bwt.fit4 = lm(bwt ~ gestation * OD + weight, data = Babies.df[-c(239, 820), ])
summary(bwt.fit4)
bwt.fit5 = lm(bwt ~ gestation * OD + weight + height, data = Babies.df[-c(239, 820), ])
summary(bwt.fit5)
bwt.fit6 = lm(bwt ~ gestation * OD + weight + height + bmi,
              data = Babies.df[-c(239, 820), ]) # weight和height与bmi同时在模型中，可能导致共线性
summary(bwt.fit6) # 注意weight, height, bmi的显著性可能下降
bwt.fit7 = lm(bwt ~ gestation * OD + height + bmi, # 移除weight，保留height和bmi
              data = Babies.df[-c(239, 820), ])
summary(bwt.fit7)
bwt.fit8 = lm(bwt ~ gestation * OD + height + bmi + not.first.born,
              data = Babies.df[-c(239, 820), ])
summary(bwt.fit8)
bwt.fit9 = lm(bwt ~ gestation * OD + height + bmi + not.first.born + smokes,
              data = Babies.df[-c(239, 820), ]) # 最终模型
summary(bwt.fit9)
plot(bwt.fit9, which = 1) # 最终模型的诊断
cooks20x(bwt.fit9)
normcheck(bwt.fit9)
confint(bwt.fit9) # 最终模型参数的置信区间

# --- 这部分代码切换到果蝇数据，与前面的婴儿体重数据无关 ---
# 在这项研究中，我们观察雄性果蝇的寿命与其
# 生殖活动的关系。
Fruitfly.df = read.csv("Fruitfly.csv", stringsAsFactors=TRUE) # 读取果蝇数据
plot(days ~ group, data = Fruitfly.df) # 寿命对分组的箱线图
# + "G1": 独居雄性,
# + "G2": 与1只感兴趣的雌性同住的雄性,
# + "G3": 与8只感兴趣的雌性同住的雄性,
# + "G4": 与1只不感兴趣的雌性同住的雄性,
# + "G5": 与8只不感兴趣的雌性同住的雄性,
summaryStats(days ~ group, Fruitfly.df) # 按组计算描述统计
ff.fit = lm(days ~ group, data = Fruitfly.df) # 单因素方差分析模型
summary(ff.fit) # 查看模型摘要
anova(ff.fit) # 查看方差分析表

# --- 这部分是关于多重比较问题的模拟，与前面的具体数据集分析目的不同 ---
m = 6 # 类别数量
n = 30 # 每个类别中的样本量
count1 = 0
for (i in 1:1000){ # 模拟1000次
  y = rnorm(m*n, mean = 0, sd = 1) # 生成数据 (所有组均值都为0)
  w = rep(LETTERS[1:m], each = n) # 创建分组变量
  table = aggregate(y, list(w), FUN=mean) # 计算各组均值
  min.index = which.min(table$x) # 找到均值最小的组
  max.index = which.max(table$x) # 找到均值最大的组
  sim_data = data.frame(y=y, w = w)
  # model = lm(formula = y~w, data = sim_data)
  # 将均值最小和最大的组作为对比的基准 (这是一种特定的比较策略，可能用于放大差异)
  w = factor(w, levels = unique(LETTERS[c(min.index,max.index, (1:m)[-c(min.index, max.index)])])) # 重新定义因子水平顺序
  sim_data = data.frame(y=y, w = w)
  model = lm(formula = y~w, data = sim_data)
  summary(model)
  # model = lm(formula = y~w, data = sim_data,
  #           subset = (w==(LETTERS[min.index])|w==(LETTERS[max.index]))) # 这行被注释掉了
  # 检查第二个系数（通常是与基准组的第一个比较）的置信区间是否包含0
  # 这里可能是想看在真实均值无差异的情况下，随机抽样有多少次会“发现”显著差异
  # 注意：这里count1的逻辑比较复杂，它是在测试第二个系数的置信区间是否覆盖0
  # 如果真实情况是所有组均值相同，那么任何比较的真实差异都是0。
  # 如果置信区间包含0，则表示未拒绝H0: diff=0。
  # 所以这里count1如果统计的是 (confint(model)[2,1] < 0 & confint(model)[2,2] > 0)，即区间包含0，
  # 那么 count1/1000 应该是对 "在H0为真时，未能拒绝H0的比例"，但这不直接是alpha或beta。
  # 如果是 !as.numeric(...) 则是在统计第一类错误的发生率。
  # 原始代码 as.numeric(...) 表示CI包含0的次数。
  count1 = count1 + as.numeric(confint(model)[2,1] < 0 & confint(model)[2,2] > 0)
}
count1/1000 # 结果应接近0.95，如果count1是统计“CI包含0的次数”

# --- 另一段模拟代码，关于置信区间覆盖真实参数的比例 ---
sample.size = 20
x = 1:sample.size;
beta0 = 3; beta1 = 0.2; beta2 = 0.1 # 真实参数
m = 10000 # 模拟次数
count0 = 0 # 记录beta0的CI覆盖真实值的次数
count1 = 0 # 记录beta1的CI覆盖真实值的次数
count2 = 0 # 记录beta2的CI覆盖真实值的次数
count = 0 # 记录所有参数的CI同时覆盖真实值的次数
for (i in 1:m){
  error = rnorm(n = sample.size, mean = 0, sd = 3)
  y = beta0 + beta1 * x + beta2 * x^2 + error # 二次模型
  sim_data = data.frame(x=x, y=y)
  model = lm(formula = y~x+I(x^2), data = sim_data) # 拟合二次模型
  # confint(model) # 这里不需要打印
  count0 = count0 + as.numeric(confint(model)[1,1] < beta0 & confint(model)[1,2] > beta0)
  count1 = count1 + as.numeric(confint(model)[2,1] < beta1 & confint(model)[2,2] > beta1)
  count2 = count2 + as.numeric(confint(model)[3,1] < beta2 & confint(model)[3,2] > beta2)
  count = count + as.numeric( # 同时覆盖
    confint(model)[1,1] < beta0 & confint(model)[1,2] > beta0
    &
      confint(model)[2,1] < beta1 & confint(model)[2,2] > beta1
    &
      confint(model)[3,1] < beta2 & confint(model)[3,2] > beta2
  )
}
count0/m # beta0的CI覆盖率，应接近0.95
count1/m # beta1的CI覆盖率，应接近0.95
count2/m # beta2的CI覆盖率，应接近0.95
count/m # 所有参数联合CI覆盖率，会低于0.95 (Bonferroni不等式相关概念)

# --- 回到果蝇数据，使用emmeans进行多重比较 ---
library(emmeans) # 加载emmeans包
Fruitfly.emm = emmeans(ff.fit, ~group) # 计算各组的边际均值
# 查看所有成对比较：
pairs(Fruitfly.emm, infer=TRUE) # infer=T 会给出调整后的p值和置信区间 (默认Tukey)
# 仅查看在5%水平下显著的比较：
Fruitfly.pairs = data.frame(pairs(Fruitfly.emm, infer=T)) # 转换为数据框以便筛选
subset(Fruitfly.pairs, p.value<0.05) # 筛选p值小于0.05的比较

Lecture 9：双因子方差分析 (Two-way ANOVA)

这个lecture深入探讨了包含两个因子（分类）解释变量的线性模型，即双因素方差分析 (Two-way ANOVA)。核心内容包括交互作用的识别、建模、解释以及不同参数化方式的理解。这与教材 STATS201 book SWU 2023.pdf 第12章“包含两个解释因子变量的线性模型（双因素方差分析）”的内容完全对应。

交互作用图 (Interaction Plots):
- 使用
```
interactionPlots(Response ~ FactorA + FactorB, data = df)
```
  (来自
```
s20x
```
  包) 来可视化两个因子变量对一个数值响应变量的联合影响。
- 图中的线条代表一个因子的不同水平，x轴是另一个因子的水平，y轴是响应变量的均值。
- 如果线条不平行，则暗示两个因子之间可能存在交互作用，意味着一个因子对响应变量的影响方式取决于另一个因子的水平。如果线条大致平行，则交互作用可能不显著。
- 教材第12章 (第9-11页) 展示并解释了这种图。
双因素ANOVA模型的拟合与检验:
- 交互作用模型
  
  ：首先拟合包含交互作用项的模型：
```
lm(Exam ~ Attend * Pass.test, data = Stats20x.df)
```
  ，这等价于
```
lm(Exam ~ Attend + Pass.test + Attend:Pass.test, ...)
```
  。
- 检验交互作用
  
  ：使用
```
anova(Exam.fit)
```
  查看方差分析表。交互作用项 (如
```
Attend:Pass.test
```
  ) 的F检验的P值用于判断交互作用是否显著。
- 模型简化
  
  ：如果交互作用不显著 (P值较大)，则根据奥卡姆剃刀原则，移除交互作用项，拟合
  
  主效应模型(或称加性模型)：
```
lm(Exam ~ Attend + Pass.test, data = Stats20x.df)
```
  。然后进一步检查各主效应的显著性。
- 代码中首先分析了 Attend 和 Gender 的模型，发现交互作用不显著，然后逐步简化。之后分析了 Attend 和 Pass.test，发现交互作用显著。
- 教材第12章 (第16页，第33-34页) 讨论了交互作用的检验和模型简化。
模型参数化与解释:
- 参考水平模型 (哑变量编码)：summary(Exam.fit) 显示的系数是相对于各因子的基准水平的。交互作用项的系数表示当两个因子都处于非基准水平时，相对于仅考虑主效应的额外效应或协同效应。教材第12章 (第18页，第40页) 有详细解释。
- 单元格均值模型 (Group Means Model)：通过
```
lm(Exam ~ Attend:Pass.test - 1, ...)
```
  可以直接估计每个因子组合（单元格）的均值。代码中演示了这种模型的系数 (
```
mu_ij
```
  ) 与参考水平模型系数 (
```
beta_k
```
  ) 之间的关系。教材第12章 (第19页) 提到了这种模型。
- 效应模型 (Effects Model)：另一种参数化是将各效应表示为与总体均值的偏差 (主效应 αi,πj) 和交互效应 (alphapiij)。代码中手动计算了这些效应，并与 emmeans 的输出进行了概念上的联系。教材第12章 (第46-48页) 讨论了这种参数化。

多重比较 (Pairwise Comparisons):

当交互作用显著时，通常我们关心的是在某个因子的特定水平下，另一个因子不同水平之间的差异；或者比较特定的因子组合。
emmeans 包用于计算调整后的边际均值 (Estimated Marginal Means) 并进行两两比较。

pairs(emmeans(Exam.fit, ~Attend*Pass.test), infer=T)

      会给出所有因子组合的两两比较，并使用Tukey等方法调整P值和置信区间以控制族错误率 (family-wise error rate)。

   - `displayPairs()` (来自 `s20x` 包) 可以更清晰地展示特定条件下的两两比较。

   - 教材第12章 (第22-25页) 详细介绍了如何使用 `emmeans` 和 `displayPairs`。

总结：Lecture 9 详细介绍了双因素方差分析的完整流程，从可视化交互作用、拟合模型、检验交互作用的显著性，到不同模型参数化的理解和使用 `emmeans` 进行多重比较，这些都是分析具有多个分类预测变量数据的重要方法。

```r
# 我们希望确定规律上课
# 并且通过测试是否与考试成绩相关。
# 我们已经分别看到
# 通过测试和规律上课
# 会增加取得好考试成绩的机会
library(s20x) # 加载s20x包
Stats20x.df = read.table("STATS20x.txt", header = T) # 读取学生数据
head(Stats20x.df) # 查看数据前几行
interactionPlots(Exam ~ Attend + Gender, data = Stats20x.df) # 绘制 Exam 对 Attend 和 Gender 的交互作用图
# 平行线表明没有交互作用
Exam.gender.fit = lm(Exam ~ Attend*Gender, data = Stats20x.df) # 拟合 Attend 和 Gender 的交互作用模型
plot(Exam.gender.fit, which = 1) # 残差图
normcheck(Exam.gender.fit) # 正态性检查
cooks20x(Exam.gender.fit) # 影响点检查
anova(Exam.gender.fit) # 方差分析表，检查交互作用项 Attend:Gender 的显著性
summary(Exam.gender.fit) # 注意这里的p值与anova表中交互作用项的p值应一致
Exam.gender.no.intact.fit = lm(Exam ~ Attend+Gender, data = Stats20x.df) # 如果交互作用不显著，拟合主效应模型
anova(Exam.gender.no.intact.fit) # 主效应模型的方差分析表
summary(Exam.gender.no.intact.fit) # 主效应模型的摘要
Exam.attend.fit = lm(Exam ~ Attend, data = Stats20x.df) # 如果Gender也不显著，进一步简化模型
summary(Exam.attend.fit)

# 现在考虑二元的test结果和出勤情况
# 所以，我们需要使用`Test`变量
# 创建变量`Pass.test`
Stats20x.df$Pass.test = factor(
  ifelse(Stats20x.df$Test >= 10, "pass", "nopass")) # Test>=10为pass，否则为nopass
# 检查新变量`Pass.test`是否正确生成
min(Stats20x.df$Test[Stats20x.df$Pass.test == "pass"])
max(Stats20x.df$Test[Stats20x.df$Pass.test == "nopass"])
interactionPlots(Exam ~ Pass.test + Attend, data = Stats20x.df) # Exam 对 Pass.test 和 Attend 的交互作用图
# 也反过来看交互作用图：
interactionPlots(Exam ~ Attend + Pass.test, data = Stats20x.df) # Exam 对 Attend 和 Pass.test 的交互作用图
# 通过测试的学生的考试分数
# 比未通过测试的学生的分数要高。
# 然而，这种差异对于那些
# 规律上课的学生来说似乎更大，
# 这可以从交互图中不平行的彩色线条看出。
# 换句话说，通过测试的影响似乎
# 因出勤组而异，这表明
# 两个预测变量之间可能存在交互作用。
Exam.fit = lm(Exam ~ Attend * Pass.test, data = Stats20x.df) # 拟合Attend和Pass.test的交互作用模型
# 模型公式也可以是 `Exam ~ Attend + Pass.test + Attend:Pass.test`
plot(Exam.fit,1) # 残差图
normcheck(Exam.fit) # 正态性检查
cooks20x(Exam.fit) # 影响点检查
anova(Exam.fit) # 查看交互作用 Attend:Pass.test 是否显著
1-30968.4/(7630.8+11076.9+909.7+30968.4) # 手动计算R^2 ( (TSS-RSS)/TSS )
summary(Exam.fit) # 模型摘要
# 组均值模型 (无整体截距，为每个组合估计一个均值)
Exam.fitNoBaseline=lm(
  Exam~Attend:Pass.test-1,data=Stats20x.df) # Attend:Pass.test-1 表示所有组合的均值
summary(Exam.fitNoBaseline)
# 参数化：beta (效应编码/哑变量编码) 和 mu_ij (单元格均值编码) 之间的关系 (参考水平)
beta0 = coef(Exam.fit)[1] # 基准组(AttendNo, TestNopass)的均值
beta1 = coef(Exam.fit)[2] # AttendYes相对于AttendNo的效应 (当TestNopass时)
beta2 = coef(Exam.fit)[3] # TestPass相对于TestNopass的效应 (当AttendNo时)
beta3 = coef(Exam.fit)[4] # 交互作用效应
mu11 = coef(Exam.fitNoBaseline)[1] # AttendNo,TestNopass 的均值
print(c(mu11,beta0)) # mu11 应该等于 beta0
mu21 = coef(Exam.fitNoBaseline)[2] # AttendYes, TestNopass 的均值
print(c(mu21,beta1+beta0)) # mu21 应该等于 beta0+beta1
mu12 = coef(Exam.fitNoBaseline)[3] # AttendNo, TestPass 的均值
print(c(mu12,beta2+beta0)) # mu12 应该等于 beta0+beta2
mu22 = coef(Exam.fitNoBaseline)[4] # AttendYes, TestPass 的均值
print(c(mu22,beta3+beta2+beta1+beta0)) # mu22 应该等于 beta0+beta1+beta2+beta3
# 多重比较
library(emmeans) # 加载emmeans包
Exam.pairs = pairs(
  emmeans(Exam.fit, ~Attend*Pass.test), infer=T) # 计算所有处理组合的边际均值并进行两两比较
Exam.pairs
# 效应参数化 (与整体均值的偏差)
mu = mean(Stats20x.df$Exam) # 总体均值
mu1dot = mean(c(mu11,mu12)) # AttendNo的边际均值 (平均了Pass.test的水平)
mu2dot = mean(c(mu21,mu22)) # AttendYes的边际均值
emmeans(Exam.fit,~Attend) # 使用emmeans计算Attend的边际均值
mudot1 = mean(c(mu11,mu21)) # TestNopass的边际均值 (平均了Attend的水平)
mudot2 = mean(c(mu12,mu22)) # TestPass的边际均值
emmeans(Exam.fit,~Pass.test) # 使用emmeans计算Pass.test的边际均值

# 行效应 (Attend的效应)
alpha1 = mu1dot - mu # AttendNo的效应 = AttendNo的边际均值 - 总体均值
alpha2 = mu2dot - mu # AttendYes的效应
# 列效应 (Pass.test的效应)
pi1 = mudot1 - mu # TestNopass的效应
pi2 = mudot2 - mu # TestPass的效应
# 交互作用效应
alphapi11 = mu11 - mu - alpha1 - pi1 # AttendNo & TestNopass 的交互效应
alphapi21 = mu21 - mu - alpha2 - pi1 # AttendYes & TestNopass 的交互效应
alphapi12 = mu12 - mu - alpha1 - pi2 # AttendNo & TestPass 的交互效应
alphapi22 = mu22 - mu - alpha2 - pi2 # AttendYes & TestPass 的交互效应

Lecture 10：广义线性模型 (Generalized Linear Models) - Poisson 和 Binomial 回归

这个lecture主要介绍广义线性模型 (Generalized Linear Models, GLMs)，特别是用于处理计数数据 (count data) 的 Poisson回归和用于处理比例/二元数据 (proportion/binary data) 的 Binomial回归 (Logistic回归)。它强调了在响应变量不满足正态分布和方差齐性假设时，直接使用普通线性模型（LM）的局限性，并引入了GLM作为更合适的工具。这与教材 STATS201 book SWU 2023.pdf 第13章“使用泊松分布建模计数数据”和第15章“使用二项分布建模比例数据”的内容一致。

计数数据的特点与分布:
- Poisson 分布
  
  : 介绍Poisson分布是描述在一定时间或空间内随机独立事件发生次数的经典概率分布，其特点是均值等于方差 (
  
  μ=σ2
  
  )。代码通过
```
dpois()
```
  和
```
rpois()
```
  展示了Poisson分布的形状如何随均值μ变化，并与正态分布进行比较，说明当μ较小时，Poisson分布是右偏的，当μ较大时，它近似于正态分布。这对应教材第13章“泊松分布” (第20-27页)。
- Binomial 分布: 简要提及了二项分布（dbinom()），并与正态分布比较，为后续的Logistic回归做铺垫。
传统线性模型 (LM) 处理计数数据的局限性:
- 直接用LM拟合计数数据（如 y ~ x，其中y是计数）通常不合适，因为计数数据往往存在异方差（方差随均值变化）且响应变量非负整数。残差图会显示问题。
- 对响应变量取对数后用LM拟合 (lm(log(Number) ~ Year, ...)），即对数-线性模型，是一种常用技巧。这种模型解释的是响应变量的中位数的乘性变化。教材第6章已详细讨论。
- 代码通过CRAN R包提交数量的例子，展示了先使用
```
lm(log(Number) ~ Year)
```
  的方法，并解释了其系数和预测。
- 但这种方法也有缺点：log(0)无定义；对数转换可能无法完全解决异方差和正态性问题；影响点在对数尺度上可能与原始尺度不同。教材第13章 (第48页) 讨论了LM处理计数数据的局限性。
Poisson 回归 (GLM):
- 模型形式
  
  : 假设响应变量Y服从Poisson分布，其均值μ=E[Y∣X]与解释变量X的关系通过连接函数 (link function)建立。对于Poisson回归，默认的连接函数是对数连接 (log link): log(μ)=β0+β1X。这意味着μ=exp(β0+β1X)，因此解释变量对均值μ的影响是乘性的。这与教材第13章 (第30页) 的描述一致。
- R实现
  
  : 使用
```
glm(Number ~ Year, family = poisson, data = ...)
```
  。
- 解释: 系数β1的指数exp(β1)表示当X增加一个单位时，响应变量均值μ的乘性变化因子。(exp(β1)−1)×100%是均值的百分比变化。
- 模型诊断 - 过离散 (Overdispersion): Poisson分布假设均值等于方差。如果实际数据中方差远大于均值，则存在过离散。这可以通过比较模型的残差离散度 (Residual Deviance)与其自由度 (Residual df)来初步判断。如果残差离散度 / 自由度 >> 1，或者
```
1 - pchisq(deviance, df.residual)
```
  的p值很小，则可能存在过离散。教材第13章 (第35页) 讨论了此检验。
- 处理过离散 - Quasi-Poisson
  
  : 如果存在过离散，可以使用
```
family = quasipoisson
```
  重新拟合模型。这会调整参数估计的标准误，从而影响p值和置信区间，但系数估计本身不变。教材第13章 (第36-39页) 详细说明了Quasi-Poisson。

GLM的预测:

predict(glm_fit, newdata, type = "link") 给出线性预测子 log(μ^) 的值。

predict(glm_fit, newdata, type = "response")

      给出响应尺度上μ^的值 (exp(log(μ^)))。 

   - `predictGLM()` (来自 `s20x` 包) 可以方便地给出响应尺度上的预测值及其置信区间。

5. **GLM应用于多解释变量**:

   - 数值与因子变量的交互作用 (地震数据)

     : 与LM类似，可以在GLM中包含数值和因子变量及其交互作用，如 

glm(Freq ~ Locn * Magnitude, family = poisson, ...)

  。解释方式也类似，但关注的是对均值的乘性效应和log-odds（对于二项）的线性效应。教材第14章 (第5-11页) 用地震数据为例。 

- 双因子模型 (鲷鱼数据)

  : 类似于双因素ANOVA，但使用 

family = poisson

  。首先检查交互作用，如果不显著则简化为主效应模型。解释时，关注各因子水平对响应变量均值的乘性影响。教材第14章 (第17-22页) 用鲷鱼数据为例。 

  

- ```
  anova(glm_fit, test="Chisq")

 (或 "F" for quasipoisson) 用于检验GLM中各项的显著性，特别是因子变量或交互作用。

总结：Lecture 10 是从传统线性模型向广义线性模型过渡的关键一课，重点介绍了Poisson回归作为分析计数数据的标准方法，包括其模型设定、参数解释、过离散问题的识别与处理，以及如何将其应用于包含多种类型解释变量的场景。

library(s20x) # 加载s20x包
# 二项分布 (Binomial Distribution)
p = 0.75 # 成功的概率
for (i in seq(10, 100, by =5)){ # 试验次数n从10到100，步长为5
  n = i; y = 0:n # 可能的成功次数
  fy = dbinom(y,size = n,prob = p) # 计算二项分布的概率质量函数
  plot(y,fy, type = "h", main = paste0("n=",n)) # 绘制概率分布图
  # 正态分布曲线比较 (二项分布的正态近似)
  lines(y,dnorm(y, mean = n*p, sd = sqrt(n*p*(1-p))), col = "red") # 均值=np, 标准差=sqrt(np(1-p))
  points(y, fy, pch = 19, cex = 0.25, col = "blue")
  legend("topleft", c("Normal", "Binomial"),
         col = c("red","blue"), pch = c(1, 19))
}
# 泊松分布 (Poisson Distribution)
y = seq(0, 100, by = 1) # 可能的计数值
for (mu in seq(0.5, 60, by = 5)){ # 均值mu从0.5到60
  fy = dpois(y,lambda = mu) # 计算泊松分布的概率质量函数
  plot(y,fy, type = "h", main = paste0("mu=",mu))
  # 正态分布曲线比较 (泊松分布的正态近似，当mu较大时)
  lines(y,dnorm(y, mean = mu, sd = sqrt(mu)), col = "red") # 均值=mu, 标准差=sqrt(mu)
  points(y, fy, pch = 19, cex = 0.25, col = "blue")
  legend("topright", c("Normal", "Poisson"),
         col = c("red","blue"), pch = c(1, 19))
}
# 正态分布并非万能
# 当mu很小时，泊松分布与正态分布差异明显
mu = 0.5
y = seq(0, 6, by = 1)
fy = dpois(y,lambda = mu)
ny = dnorm(y, mean = mu, sd = sqrt(mu))
plot(y, ny, type = "b", col = "red", ylab = "fy",
     main = "Normal Vs Poisson (mu=0.5)", ylim = c(0,0.6))
points(y, fy, pch = 19, cex = 0.5, col = "blue")
segments(y,0,y,fy, col = "blue")
legend("topright", c("Normal", "Poisson"),
       col = c("red","blue"), pch = c(1, 19))
# 当n很小或p接近0或1时，二项分布与正态分布差异明显
p = 0.75
n = 6; y = 0:n
fy = dbinom(y,size = n,prob = p)
ny = dnorm(y, mean = n*p, sd = sqrt(n*p*(1-p)))
plot(y,ny, type = "b", col = "red",ylim = c(0,0.4),
     main = "Normal Vs Binomial (n=6,p=0.75)")
points(y, fy, pch = 19, cex = 0.5, col = "blue")
segments(y,0,y,fy, col = "blue")
legend("topleft", c("Normal", "Binomial"),
       col = c("red","blue"), pch = c(1, 19))

# 在回归中差异更大
x = -30:30
beta0 = 0.3
beta1 = 0.1
mu = exp(beta0 + beta1* x) # 泊松回归的均值通常通过指数连接函数建模
y = rpois(length(mu),lambda = mu) # 生成泊松分布的响应变量
sim.df = data.frame(x=x, y=y)
# 必须使用灵活的线性模型 (如果用普通LM)
fit.normal = lm(y~x, data = sim.df) # 普通线性模型
plot(fit.normal, which = 1) # 残差图可能显示异方差和非线性
fit.quadratic.normal = lm(y~x+I(x^2), data = sim.df) # 二次模型
plot(fit.quadratic.normal, which = 1)
fit.cubic.normal = lm(y~x+I(x^2)+I(x^3), data = sim.df) # 三次模型
plot(fit.cubic.normal, which = 1)
fit.quartic.normal = lm(y~x+I(x^2)+I(x^3)+I(x^4), data = sim.df) # 四次模型
plot(fit.quartic.normal, which = 1)
# 通常拟合线会弯弯曲曲
plot(x,y)
lines(x, fitted.values(fit.quadratic.normal), col = "red")
plot(x,y)
lines(x, fitted.values(fit.cubic.normal), col = "red")
plot(x,y)
lines(x, fitted.values(fit.quartic.normal), col = "red")

# 正确的泊松假设
fit.poisson = glm(y~x, family = poisson, data = sim.df) # 使用glm和poisson族
summary(fit.poisson)
beta0;beta1 # 真实参数值
plot(x,y, main = "Poisson data")
lines(x,predict(fit.poisson, type = "response"), col = "blue") # 泊松回归拟合线 (响应尺度)
lines(x, fitted.values(fit.quartic.normal), col = "red") # 普通LM(四次)拟合线
legend("topleft", c("Normal", "Poisson"),
       col = c("red","blue"), lty = 1)
# 不仔细看差别不大
summaryStats(fitted.values(fit.quartic.normal)) # 普通LM的拟合值可能为负
# 当扩展到给定数据范围之外时，问题更大
x.plot = -60:60 # 更宽的x范围用于外推
mu.plot = exp(0.3 + 0.1* x.plot)
y.plot = rpois(length(mu.plot),lambda = mu.plot)
y.pois = predict(fit.poisson, newdata = data.frame(x=x.plot),type = "response")
y.norm = predict(fit.quartic.normal, newdata = data.frame(x=x.plot))
# 普通LM外推非常不可靠
plot(x.plot, y.plot, main = "Beyond Observed Poisson data")
lines(x.plot, y.pois, col = "blue") # 泊松回归外推
lines(x.plot, y.norm, col = "red") # 普通LM外推
legend("topleft", c("Normal", "Poisson"),
       col = c("red","blue"), lty = 1)

# setwd("~/Desktop") # 设置工作目录 (根据用户实际情况)
CRAN.df = read.table("CRAN.txt", header=T) # 读取CRAN R包提交数据
CRAN.df
## 原始y的散点图
plot(Number ~ Year, data = CRAN.df)
## log(y)的散点图
plot(log(Number) ~ Year, data = CRAN.df)
CRAN.fit = lm(log(Number) ~ Year, data = CRAN.df) # 对log(Number)拟合线性模型
plot(CRAN.fit,which=1) # 残差图
normcheck(CRAN.fit) # 正态性检查
cooks20x(CRAN.fit) # 影响点检查
summary(CRAN.fit)
exp(CRAN.fit$coef["Year"]) # 年份的乘性效应因子 (中位数)
## 置信区间
100*(exp(confint(CRAN.fit)) - 1) # 年份效应的百分比变化 (中位数)
predCRAN.df = data.frame(Year = 2017) # 预测2017年
pred2017 = predict(CRAN.fit, predCRAN.df, interval = "confidence")
## 对数尺度上的预测
pred2017
## 反转换得到2017年提交数量的中位数预测
exp(pred2017)

# 泊松拟合
CRAN.pois.fit = glm(Number ~ Year, family = poisson, data = CRAN.df) # 使用glm进行泊松回归
summary(CRAN.pois.fit)
# 如果泊松假设为真，残差应近似标准正态
plot(CRAN.pois.fit, which = 1) # 查看残差图 (注意glm的残差类型与lm不同)
# 离散度检验：原假设是模型充分（即泊松假设适合，特别是均值=方差）
# 通常查看残差离散度 (Residual Deviance) 与自由度的比值
1 - pchisq(402.61,10) # summary(CRAN.pois.fit)$deviance, summary(CRAN.pois.fit)$df.residual
# p值非常小，表明模型不充分，可能存在过离散 (overdispersion)

# 补救措施：使用类泊松 (quasipoisson)
CRAN.quasi.pois.fit = glm(
  Number ~ Year, family = quasipoisson, data = CRAN.df)
summary(CRAN.quasi.pois.fit) # 注意此时会估计一个离散参数 (Dispersion parameter)
# 解释
exp(CRAN.quasi.pois.fit$coef["Year"]) # 年份的乘性效应因子 (均值)
100*(exp(confint(CRAN.quasi.pois.fit))[2,] - 1) # 年份效应的百分比变化 (均值)
100*(exp(confint(CRAN.fit))[2,] - 1) # 与之前log(LM)的结果比较 (解释的是中位数)
# 预测
new.CRAN.df = data.frame(Year = 2017)
predictGLM(CRAN.quasi.pois.fit, new.CRAN.df) # 预测 (默认link尺度，即log(均值))
pred2017.quasi=predict(CRAN.quasi.pois.fit, new.CRAN.df, se.fit=TRUE) # 获取预测值和标准误
# log(均值)的置信区间
lower = pred2017.quasi$fit-1.96*pred2017.quasi$se.fit
upper = pred2017.quasi$fit+1.96*pred2017.quasi$se.fit
# 均值的置信区间
pred2017.ci.mean=exp(c(lower, upper))
pred2017.ci.mean
# exp(predictGLM(CRAN.quasi.pois.fit, new.CRAN.df)) # 等价于上面的手动计算
predictGLM(CRAN.quasi.pois.fit, new.CRAN.df, type="response") # 直接在响应尺度上预测和获取CI

# 泊松回归的预测区间不作考核
# --- 处理数值和分类变量 (地震数据) ---
Quakes.df=read.table("EarthquakeMagnitudes.txt",header=TRUE) # 读取地震数据
Quakes.df$Locn=as.factor(Quakes.df$Locn) # 将地点转换为因子
subset(Quakes.df,subset=c(Locn=="SC"))[1:4,] # 打印南加州前4行
subset(Quakes.df,subset=c(Locn=="WA"))[1:4,] # 打印华盛顿州前4行
plot(Freq~Magnitude,data=Quakes.df,pch=substr(Locn,1,1)) # 频数对震级的散点图，按地点区分
Quake.fit = glm(Freq ~ Locn * Magnitude, # 拟合带交互作用的泊松回归
                 family = poisson, data = Quakes.df)
plot(Quake.fit, which = 1) # 残差图
plot(Quake.fit, which = 4) # Cook's距离图
1 - pchisq(summary(Quake.fit)$deviance, summary(Quake.fit)$df.residual) # 离散度检验 (p值大，模型可接受)
summary(Quake.fit)
# 南加州的震级效应
Quake.cis = confint(Quake.fit)
100*(exp(Quake.cis[3,]) - 1) # 震级每增加1，频数均值变化的百分比 (SC)
# 更改基准到华盛顿州
Quakes.df$Locn2=factor(Quakes.df$Locn,levels=c("WA","SC"))
Quake2.fit=glm(Freq~Locn2*Magnitude,family=poisson,data=Quakes.df)
Quake.WA.ci = confint(Quake2.fit)
100*(exp(Quake.WA.ci[3,]) - 1) # 震级每增加1，频数均值变化的百分比 (WA)
# 展示结果的最佳方式
no.sc = predictGLM(Quake.fit, subset(Quakes.df,subset=c(Locn=="SC")),
                   type="response") # 预测SC的频数均值
mag.sc = subset(Quakes.df,subset=c(Locn=="SC"))$Magnitude
no.was = predictGLM(Quake.fit, subset(Quakes.df,subset=c(Locn=="WA")),
                   type="response") # 预测WA的频数均值
mag.was = subset(Quakes.df,subset=c(Locn=="WA"))$Magnitude
plot(Freq~Magnitude,data=Quakes.df,pch=substr(Locn,1,1))
lines(mag.sc, no.sc[,1], col = "blue") # 绘制SC的拟合线
lines(mag.was, no.was[,1], col = "red") # 绘制WA的拟合线
legend("topright", c("Southern California", "Washington"),
       lty = 1, col = c("blue", "red"))

# --- 鲷鱼数据 (两个分类变量)，类似于双因素方差分析 ---
Snap.df = read.table("SnapperCROPvsHAHEI.txt", header = TRUE) # 读取鲷鱼数据
interactionPlots(Freq ~ Locn * Reserve, data = Snap.df) # 交互作用图 (注意是原始频数)
# 从交互作用模型开始
Snap.glm = glm(Freq ~ Locn * Reserve, family = poisson, data = Snap.df)
summary(Snap.glm)
1 - pchisq(summary(Snap.glm)$deviance, summary(Snap.glm)$df.residual) # 离散度检验 (p值大，模型可接受)
anova(Snap.glm, test="Chisq") # 检验交互作用的显著性 (Chisq检验用于GLM)
Snap2.glm = glm(Freq ~ Locn + Reserve, family = poisson, data = Snap.df) # 如果交互不显著，拟合主效应模型
anova(Snap2.glm, test="Chisq") # 主效应模型的ANOVA表
1 - pchisq(summary(Snap2.glm)$deviance, summary(Snap2.glm)$df.residual) # 再次检查离散度
summary(Snap2.glm)
plot(Snap2.glm, which = 1) # 残差图
100*(exp(confint(Snap2.glm)) - 1) # 解释主效应 (均值的百分比变化)

Lecture 11

这个lecture主要讲解Logistic回归，它是广义线性模型的一种，专门用于处理二元（是/否，0/1）响应变量或比例数据（成功次数/总试验次数）。核心概念包括odds、log-odds以及如何解释模型系数。这与教材 STATS201 book SWU 2023.pdf 第15章“使用二项分布建模比例数据”和第16章“列联表分析” 的内容相关。

这个lecture全面介绍了广义线性模型 (GLM) 的另一个重要分支：Logistic回归，用于分析二元响应变量或比例数据。同时，它也开始引入列联表分析的概念，并展示了Poisson回归和Logistic回归在特定情况下（饱和模型分析关联性）的等价性。

二元数据与Binomial/Bernoulli分布:
- 当响应变量只有两个可能的结果（如成功/失败，是/否，0/1）时，称为二元数据 (binary data)。单次试验服从Bernoulli分布。多次独立重复的Bernoulli试验中成功次数服从Binomial分布。教材第15章 (第4-5页) 对此有介绍。
- 代码中篮球投篮数据 (bb.df) 的 basket 变量 (0或1) 是典型的二元数据。
Odds 和 Log-Odds (Logit):
- Odds (几率)：事件发生的概率与不发生的概率之比，即Odds=p/(1−p)。
- Log-Odds (对数几率，logit)：logit(p)=log(Odds)=log(p/(1−p))。Log-odds的取值范围是(−∞,+∞)，这使得它适合作为线性模型的响应部分。
- 从log-odds反推概率p的函数是logistic函数：p=exp(log-odds)/(1+exp(log-odds))=plogis(log-odds)。
- 教材第15章 (第7-9页) 详细解释了odds和log-odds。

Logistic回归模型:

模型形式：logit(pi)=β0+β1Xi1+...+βkXik。这意味着解释变量与成功概率pi的对数几率呈线性关系。

R实现：

glm(response ~ predictors, family = binomial, data = df)

。

对于未分组的二元数据 (如 bb.df): response 是0/1变量。

对于分组数据

(如

bb.grouped.df

或

Space.df

response

可以是 

cbind(success_count, failure_count)

  。 

- 或者 

response

是成功比例，并使用 

weights = total_count

       参数。 

- 系数解释:

  - βj 表示当其他变量不变时，Xj 每增加一个单位，log(Odds) 的变化量。

  - exp(βj) 表示当其他变量不变时，Xj 每增加一个单位，Odds 的**乘性变化因子 (Odds Ratio, OR)**。

  - (exp(βj)−1)×100% 是 Odds 的百分比变化。

  - 代码中

100*(exp(coef(bb.fit2)[2])-1)

和

100*(exp(bb.ci2[2,])-1)


        就是这种解释。教材第15章 (第27-28页)。

4. **模型诊断与过离散 (针对分组数据)**:

   - 对于分组的二项数据，可以像Poisson回归一样使用残差离散度来检查模型拟合优度。如果

1 - pchisq(deviance, df.residual)


   的p值很小，可能表明存在过离散(或欠离散)。 

- 处理过离散：使用

family = quasibinomial


     。这会调整标准误和p值，但不改变系数估计。 

   - 对于未分组的二元数据，残差图和离散度检验的解释性有限。 

5. **预测**:

   - `predict(glm_fit, newdata, type = "link")` 给出log-odds尺度的预测。

   - ```
     predict(glm_fit, newdata, type = "response")

给出概率尺度的预测。

predictGLM() (来自 s20x 包) 可以方便地给出这两个尺度上的预测值及其置信区间。

挑战者号航天飞机灾难案例:
- 这是一个著名的错误应用线性模型分析比例数据导致灾难性后果的案例。直接对比例数据 (O环损坏数/总数) 用
```
lm()
```
  拟合是错误的，因为它可能预测出小于0或大于1的概率，且未考虑二项分布的特性。
- 正确的做法是使用Logistic回归 (
```
glm(cbind(Failure, 6-Failure) ~ Temp, family = binomial, ...)
```
  )。教材第15章 (第45-52页) 详细描述了此案例。
列联表分析初探:
- 当所有变量都是分类变量时，数据可以总结为列联表 (contingency table)。
- 可以使用
```
xtabs()
```
  创建列联表，并用
```
plot()
```
  (马赛克图) 或
```
barplot()
```
  可视化。
- 关联性研究:
  - Poisson回归方法
    
    : 可以将列联表中的频数作为响应变量，用
```
glm(Freq ~ FactorA * FactorB, family = poisson, ...)
```
    拟合。交互作用项的系数exp(βinteraction)即为Odds Ratio (OR)，表示一个因子水平下，另一个因子不同水平间的odds比率。
  - Logistic回归方法 (等价性)
    
    : 如果将其中一个因子视为响应（如Pass/Fail），另一个因子视为解释变量，用
```
glm(cbind(Pass_counts, Fail_counts) ~ Factor_predictor, family=binomial, ...)
```
    拟合，其解释变量的系数exp(βpredictor)也解释为Odds Ratio，且与Poisson模型交互作用项的OR在饱和模型中是等价的。
  - 代码中演示了对 AttendPass 数据分别用这两种GLM方法以及直接计算OR，结果相似。
  - 教材第16章 (第18-29页) 详细讨论了这种等价性。

总结：Lecture 11 是 GLM 的重要组成部分，系统介绍了 Logistic 回归的原理、实现、解释和预测，并通过实例（包括著名的挑战者号案例）强调了其在处理二元/比例数据时的正确性和重要性。同时，也开始将 GLM 应用于列联表的关联性分析，为更复杂的分类数据分析打下基础。

# Logistic 回归 - 篮球数据示例
library(s20x) # 加载s20x包
bb.df = read.csv("basketball.csv") # 读取篮球投篮数据
head(bb.df, 10) # 查看数据前10行
bb.fit = glm(basket ~ distance * gender, # basket(0或1) 对 距离和性别的交互作用模型
             family = binomial, data = bb.df) # 使用二项分布族 (logistic连接函数是默认)
plot(bb.fit, which = 1, lty=2) # 残差图 (对于未分组二元数据，解释性有限)
summary(bb.fit) # 查看模型摘要
1-pchisq(46.202, 56) # 离散度检验的近似 (对于未分组数据，解释需谨慎)
bb.fit1 = glm(basket ~ distance + gender, family = binomial, data = bb.df) # 移除交互作用
summary(bb.fit1)
bb.fit2 = glm(basket ~ distance, family = binomial, data = bb.df) # 仅保留距离作为预测变量
summary(bb.fit2)
100*(exp(coef(bb.fit2)[2])-1) # 距离每增加1单位，odds变化的百分比
(bb.ci2 = confint(bb.fit2)) # 系数的置信区间 (log-odds尺度)
100*(exp(bb.ci2[2,])-1) # 距离每增加1单位，odds变化百分比的置信区间

# 预测
predn.df=data.frame(distance = 1:3) # 创建新的距离值用于预测
bb.logit.pred = predict(bb.fit2, newdata = predn.df) # 预测 (默认在log-odds尺度，即线性预测子)
bb.logit.pred # 这是在log-odds尺度上
exp(bb.logit.pred) # 转换到odds尺度
exp(bb.logit.pred) / (1+exp(bb.logit.pred)) # 从odds转换到概率尺度 p = odds/(1+odds)
plogis(bb.logit.pred) # 内置函数，从log-odds转换到概率尺度 (logistic函数)
predict(bb.fit2, newdata = predn.df, type="response") # 直接在概率尺度上预测

# 概率的置信区间
bb.logit.predses = predict( # 获取log-odds尺度预测的标准误
  bb.fit2, newdata = predn.df, se.fit = TRUE)$se.fit
# log-odds的置信区间上下限
lower = bb.logit.pred - 1.96*bb.logit.predses
upper = bb.logit.pred + 1.96*bb.logit.predses
ci.logit = cbind(lower, upper) # log-odds的置信区间
# 转换为概率的置信区间
ci.prob = plogis(ci.logit)
# 或者使用s20x包中的predictGLM
predictGLM(bb.fit2, newdata = predn.df, type="link") # log-odds尺度的CI
predictGLM(bb.fit2, newdata = predn.df, type="response") # 概率尺度的CI

# 展示模型
plot(basket ~ distance, xlim = c(0,5), ylim=c(0,1), # 绘制原始0/1数据点
     ylab = "fitted values (Est prob)", data = bb.df)
distance.plot = seq(0,5, by = 0.1) # 创建平滑的距离序列
phat = predict(bb.fit2, newdata = data.frame( # 预测概率
  distance=distance.plot), type = "response")
lines(distance.plot, phat) # 绘制拟合的S形曲线
ci.plot = predictGLM(bb.fit2, newdata = data.frame( # 获取概率的置信带
  distance=distance.plot), type="response")
lines(distance.plot, ci.plot[,2], lty = 2) # 置信带下限
lines(distance.plot, ci.plot[,3], lty = 2) # 置信带上限

# 未分组 vs 分组数据
head(bb.df) # 未分组数据
success.tbl = xtabs(basket~distance+gender, data = bb.df) # 创建成功次数的列联表
success.tbl # 成功次数表
sum(success.tbl[1:6]) # 总成功次数
sum(bb.df$basket) # 与上面应一致
str(success.tbl)
(dist.unique = attr(success.tbl, "dimnames")$distance) # 获取距离的唯一值
(distance = rep(as.numeric(dist.unique), times = 2)) # 重复以匹配性别
(gender.unique = attr(success.tbl, "dimnames")$gender) # 获取性别的唯一值
(gender = rep(gender.unique, each = 3)) # 重复以匹配距离
fail.tbl = xtabs(1-basket~distance+gender, data = bb.df) # 创建失败次数的列联表
bb.grouped.df = data.frame( # 创建分组后的数据框
  success = success.tbl[1:6], fail = fail.tbl[1:6],
  distance = distance, gender = gender)
bb.grouped.fit = glm( # 使用 cbind(success, fail) 作为响应变量
  cbind(success, fail) ~ distance * gender,
  family = binomial,data = bb.grouped.df)
summary(bb.grouped.fit) # 分组数据拟合结果
summary(bb.fit) # 未分组数据拟合结果 (应相同)

# 第三种拟合logistic回归的方式 (使用比例和权重)
bb.grouped.df$n = bb.grouped.df$success + bb.grouped.df$fail # 总试验次数
bb.grouped.df$prop = bb.grouped.df$success/bb.grouped.df$n # 成功比例
bb.grouped.prop.fit = glm(
  prop ~ distance * gender, weights = n, # 使用成功比例作为响应，总次数作为权重
  family = binomial,data = bb.grouped.df)
summary(bb.grouped.prop.fit) # 结果应与前两种方式一致
summary(bb.grouped.fit)
summary(bb.fit)

# 不使用logistic回归的真正危险 (挑战者号航天飞机案例)
Space.df = read.table("ChallengerShuttle.txt", head = TRUE) # 读取挑战者号数据
Space.df # 已知有6个O型环
Space.df$prop = Space.df$Failure/6 # 计算失败比例
# 错误方法1: 移除0失败的数据点后用普通线性模型拟合
Space.no.zero.fit = lm(prop~Temp, data = subset(Space.df, Failure>0))
summary(Space.no.zero.fit)
# 错误方法2: 直接用普通线性模型拟合比例
Space.fit = lm(prop~Temp, data = Space.df)
summary(Space.fit) # 这个模型的预测可能超出[0,1]范围
plot(Space.fit, which = 1) # 残差图可能显示问题
normcheck(Space.fit) # 正态性假设不成立
cooks20x(Space.fit)
# 正确方法: logistic回归
Space.logistic.fit=glm(
  cbind(Failure, 6-Failure)~Temp, family = binomial, data = Space.df) # Failure是成功(这里指O环损坏)次数, 6-Failure是未损坏次数
summary(Space.logistic.fit)
predictGLM(Space.logistic.fit, type = "response", # 预测在31华氏度时O环损坏的概率
           newdata = data.frame(Temp=31))
plot(prop~Temp, ylim = c(0,1), xlim = c(20,100),
     data = Space.df) # 绘制原始比例数据
Temp.plot = seq(20, 100, by = 1) # 创建温度序列
FV = predictGLM(Space.logistic.fit, type = "response",
                newdata = data.frame(Temp=Temp.plot)) # 预测损坏概率
lines(Temp.plot, FV[,1], lty = 2) # 绘制拟合的logistic曲线
abline(v = 31, col = "red") # 标记挑战者号发射时的温度

# 类二项 (Quasibinomial) - 处理过离散 (当响应是比例时)
Haddock.df = read.table("Haddock.dat", head = TRUE) # 读取黑线鳕数据 (已分组)
Haddock.glm = glm(cbind(codend,cover) ~ forklen, family = binomial, # codend是网到的，cover是逃逸的
                  data = Haddock.df)
plot(Haddock.glm, which = 1)
cooks20x(Haddock.glm)
Haddock.df[6,] # 查看某个可能有影响的点
# summary(Haddock.glm) # 查看初始模型
# Haddock.glm = glm(cbind(codend,cover) ~ forklen, family = binomial, # 尝试移除影响点
#                   data = Haddock.df[-6,])
# cooks20x(Haddock.glm) # 再次检查
# 检查离散度：如果p值小，则存在过离散或欠离散
1 - pchisq(summary(Haddock.glm)$deviance,
           summary(Haddock.glm)$df.residual)
# 如果p值小，我们可以尝试 family = quasibinomial
Haddock.quasi.glm = glm(
  cbind(codend,cover) ~ forklen,
  family = quasibinomial, # 使用类二项分布族
  data = Haddock.df) # 教材中使用的是 data = Haddock.df[-6,]
summary(Haddock.quasi.glm) # 类二项模型摘要
summary(Haddock.glm) # 与二项模型比较 (系数估计相同，标准误不同)
100*(exp(confint(Haddock.glm)) - 1) # 解释系数 (odds百分比变化)
forklen.plot = seq(10, 60, by = 0.5) # 创建鱼叉长度序列
FV = predictGLM(Haddock.glm, type = "response", # 预测捕获概率
                newdata = data.frame(forklen=forklen.plot))
plot(forklen.plot, FV[,1], type = "l",
     xlab = "Fork Length (cm)", ylab = "Prob") # 绘制拟合的logistic曲线
prop = Haddock.df$codend/(Haddock.df$codend+Haddock.df$cover) # 计算原始数据中的比例
points(Haddock.df$forklen, prop) # 添加原始数据点
rm(list=ls()) # 清除工作空间

# 列联表 (关联性研究)
# 例如：眼睛和头发颜色
Genetics=matrix(c(284, 577, 613, 2002),ncol=2) # 创建矩阵
rownames(Genetics) = c("Hair brown", "Hair other")
colnames(Genetics) = c("Eyes brown", "Eyes other")
gen.tbl=as.table(Genetics) # 转换为表格对象
gen.tbl
plot(gen.tbl) # 绘制马赛克图
barplot(gen.tbl) # 绘制条形图
legend("topleft", legend=rownames(gen.tbl),
       fill=grey(1:2/2))
# 疫苗和压痛程度
vaccines=matrix(c(21,16,11,2,1,22,19,9),nrow=2,byrow=T)
rownames(vaccines)=c("Trmt A","Trmt B")
colnames(vaccines)=c("none","mild","moderate","severe")
vax.tbl=as.table(vaccines)
vax.tbl
plot(vax.tbl) # 马赛克图
n.levels = ncol(vax.tbl)
barplot(t(vax.tbl), col=grey(1:n.levels/n.levels), ylim = c(0, 60)) # 转置后绘制堆叠条形图
legend("top", legend=colnames(vax.tbl), horiz = TRUE,
       fill=grey(1:n.levels/n.levels))

# 课程通过与否和出勤情况
AP.df = read.table("AttendPass.txt",header=T) # 读取出勤与通过数据
head(AP.df, 8)
AP.tbl = xtabs(~Attend+Pass, data = AP.df) # 创建列联表
barplot(t(AP.tbl),legend=TRUE) # 绘制条形图
plot(AP.tbl) # 绘制马赛克图
prop.table(AP.tbl) # 计算比例表

# 1. 多维列联表
# 2. 响应变量和解释变量可能清晰也可能不清晰
# 3. 试验次数n是否固定可能清晰也可能不清晰
# 4. 在研究关联性时这些不一定重要
# 泊松回归和二项回归在关联性研究中的等价性
freq.df = data.frame( # 将列联表转换为长格式数据框
  Y=AP.tbl[1:4], # 频数
  Attend=rep(attr(AP.tbl, "dimnames")$Attend, times = 2),
  Pass=rep(attr(AP.tbl, "dimnames")$Pass, each = 2))
AP.tbl
freq.df$Attend = factor(freq.df$Attend, levels = c("not.attend", "attend")) # 设置因子水平
freq.df$Pass = factor(freq.df$Pass)
# AP.tbl = AP.tbl[2:1,] # 这行会改变AP.tbl的行顺序，影响下面AP.grouped.df的创建，可能导致与freq.df不一致

# 拟合泊松模型 (响应变量是频数Y)
AP.pois=glm(Y~Attend*Pass,family=poisson,data=freq.df) # 注意这里freq.df的Attend顺序
summary(AP.pois)

# 拟合Logistic回归 (未分组数据)
AP.logistic = glm(
  as.numeric(Pass=="pass")~Attend, # Pass=="pass"会产生0/1响应
  family = binomial,data = AP.df)

# 拟合Logistic回归 (分组数据)
# AP.tbl的行顺序可能因上一条注释掉的命令而与freq.df不同，需要注意
AP.grouped.df = data.frame( # 从原始AP.tbl创建分组数据
  pass = AP.tbl[,2], fail = AP.tbl[,1], # 假设AP.tbl的列是 fail, pass
  Attend = rownames(AP.tbl)) # Attend是行名
AP.grouped.df$Attend <- factor(AP.grouped.df$Attend, levels = c("not.attend", "attend")) # 确保因子水平一致

AP.grouped.logistic = glm(cbind(pass,fail)~Attend,
                  family = binomial,data = AP.grouped.df) # 使用成功/失败次数

summary(AP.logistic)
summary(AP.grouped.logistic)
summary(AP.pois) # 比较三个模型的系数
confint(AP.logistic)
confint(AP.grouped.logistic)
confint(AP.pois) # 交互作用项的系数 (log-odds ratio) 应与logistic中Attend的系数相似

# 不用模型计算Odds Ratio
coef(AP.pois)
coef(AP.pois)[4] # Poisson模型中交互作用项的系数 (log odds ratio)
exp(coef(AP.pois)[4]) # Odds Ratio
AP.tbl # 原始列联表 (注意行顺序)
# (OR=(27*83)/(17*19)) # 手动计算OR ( (n00*n11)/(n01*n10) )，需确保AP.tbl顺序正确
# 例如，如果AP.tbl是:
#            Pass
# Attend     fail pass
# not.attend   27   19
# attend       17   83
# OR = (n_attend_pass * n_not.attend_fail) / (n_attend_fail * n_not.attend_pass)
# OR = (83 * 27) / (17 * 19)
(OR = (AP.tbl["attend","pass"] * AP.tbl["not.attend","fail"]) / (AP.tbl["attend","fail"] * AP.tbl["not.attend","pass"]))
logOR.se=sqrt(1/17+1/83+1/27+1/19) # log(OR)的标准误近似公式
logOR.CI=log(OR) + c(-1,1)*1.96*logOR.se # log(OR)的置信区间
exp(logOR.CI) # OR的置信区间，应与模型结果相似
exp(confint.default(AP.pois)[4,] ) # 从Poisson模型得到的OR置信区间

课件总结

Week 1

幻灯片内容翻译与概览

知识点梳理 (first_week.pdf)

Week 2

幻灯片内容翻译与概览

知识点梳理 (second_week.pdf)

Week 3

幻灯片内容翻译与概览

知识点梳理 (third_week.pdf)

Week 4

幻灯片内容翻译与概览

知识点梳理 (fourth_week.pdf)

题目总结

first week

来自 2024_test_sol.pdf (2024年春季测试题解析)

来自 test_sol(2).pdf (2025年春季测试题解析 - 即今年的测试)

代码总结

Lecture 1

Lecture 2

Lecture 3：曲线拟合与分类解释变量 (Fitting Curves and Categorical Explanatory Variables)

Lecture 4：数据转换 (Data Transformations) - 特别是Log转换

Lecture 5：幂律模型 (Power Law Models)

Lecture 6：包含数值和因子解释变量的线性模型 (Linear Models with Numeric and Factor Explanatory Variables) - 交互作用模型

Lecture 7

Lecture 8：多重线性回归与共线性问题 (Multiple Linear Regression and Multicollinearity)

Lecture 9：双因子方差分析 (Two-way ANOVA)

Lecture 10：广义线性模型 (Generalized Linear Models) - Poisson 和 Binomial 回归

Lecture 11

来自 `2024_test_sol.pdf` (2024年春季测试题解析)

来自 `test_sol(2).pdf` (2025年春季测试题解析 - 即今年的测试)