算法分析与设计
算法分析与设计
Powered by Hongyi Yang
Date:2025.12.23 16:40
[toc]
算法分析与设计
选择题12(5、6道是和算时间复杂度相关的,剩下的就是扣概念,比如说DFS使用队列BFS使用栈这个就说反了等),计算题3,简答题2,设计题1
做题全英文,中文解释不得分
忽略基础语法小错误,但是编程代码的专业术语不能错(错了扣分)
上课讲的所有例题和作业的题基本覆盖了所有的题型,期末会比较灵活有些东西不一定会见到
Part之算法时间分析(选择题不止一道,计算题一道):
计算题至少一个会算时间,最好的和最坏的(选择题里也会有大量的时间复杂度计算)考的时候不会算每一行代码怎么样而是常规的那种一个段(或者也有可能给两个代码哪个更快)L1不是重点;
L2不同函数的大小:
必考L4的两个式子的
如果考计算题大概率是ppt原题(难的,要不就是比较简单的变式)
简答题会考模棱两可的概念,比如分治、贪心和动态规划有什么区别
设计题会规定一个时间复杂度然后解题
Part之分治算法:核心还是那几个排序也就是课件9,10
分治法先写结束条件A,然后BC固定都是调用自己完成任务就行;快排就是往中间插根杆子然后两边排序;所以分治法其实是模块化写作:把A结束条件想好,然后自己套自己咋写,关键是A、BC(BC都算套自己)中间这个条件要怎么设计;那么分治法的
快速排序quick sort选了pivot就不会把这个pivot参与运算(给定的代码肯定不会考默写)快排考察点不知道两边是不是均匀分配长度的,如果选pivot就头尾中间这三个值里面选一个中间值(作业1q4这种不太可能考,只可能考课内的略微变式,写代码的时候写成伪代码即可)
Algorithm Analysis 算法时间分析
measure running time 时间复杂度的计算
1.算法的三个特征
①定义域Domain of definition:合法的输入集合。比如说FASTFIB接收的是一个自然数
②正确性Correctness:算法是否对每个合法输入都给出预期的输出。例如SLOWFIB和FASTFIB都是正确的,在输入n时都能返回第n个斐波那契数F(n)
③资源使用:算法所占用的运行时间和内存空间
算法分析是对算法资源使用严谨的(即数学层面的)研究
2.计算资源使用Computational resource use
时间:算法的执行时间execution time
空间:算法占用的内存空间
①资源使用取决于输入大小:通常随着输入变大而增加:例如F(0),……,F(5),……
②时空权衡(Time-space trade-off),运行时间通常比内存空间的使用更为重要。
3.时间复杂度的计算
(1)正常的都比较简单,比如说一个循环是n,两个
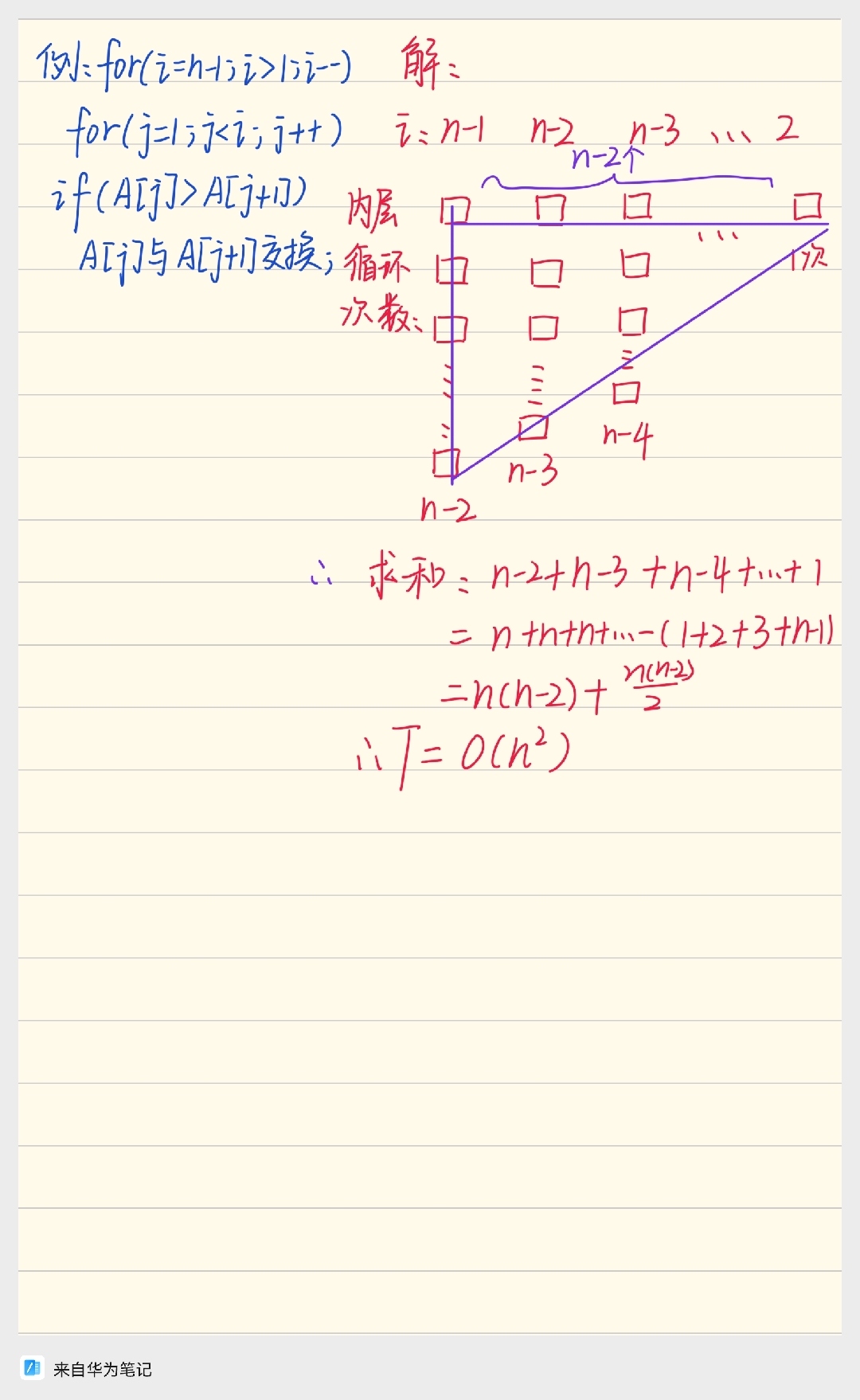
(2)具有交互变量(interacting variables)的嵌套循环
① 识别循环和变量: 确定哪个是外层循环(例如变量
② 分析内层循环: 假设外层循环正处于第
③ 建立总和 (Summation): 既然你已经知道了“每一次”外层循环
④ 求解总和: 使用你的数学知识(例如等差数列或等比数列的求和公式)来解这个总和,得到一个关于
例题
(1)
1 | for i <- 1 to n do |
①识别循环和变量
- 外层循环: 变量是
- 内层循环: 变量是
- 交互: 内层循环的起始点
②分析内层循环
我们来分析当
print 语句)执行了多少次:
- 当
- 当
- 当
- ...
- 当
因此,对于任意给定的
③建立总和
现在,我们把
总运行时间
这等价于:
④求解总和
这个求和
总运行时间
这个表达式
4.时间复杂度B站解法
(1)单层循环
①列出循环函数t及每轮循环i的变化值
②找出t和i的关系
③确定循环停止条件
④联立两式解方程
⑤写结果
例题
(1)
1 | i=n*n: |
①列出循环函数t及每轮循环i的变化值
t: 0 1 2 3 ……
i:
②找出t和i的关系
观察到
③确定循环停止条件
循环结束条件是
④联立两式解方程
联立①②
⑤写结果
综上
(2)
1 | x=0; |
t: 0 1 2 3 ……
x: 0 1 2 3 ……
联立①②得
综上
(3)
1 | int i=1 |
t: 0 1 2 3 ……
i: 1 2 4 8 ……
观察得
循环终止条件位
联立两式得
综上
(4)
1 | int i=0; |
c
观察得
终止循环条件为
联立两式得
综上
(5)
1 | y=0; |
t: 0 1 2 3 ……
y: 0 1 2 3 ……
观察得
循环终止条件为
联立得
综上
(2)两层循环
①列出外层循环中i的变化值
②列出内层语句得执行次数
③求和,写结果
例题
(1)
1 | int m=0,i,j; |
①列出外层循环中i的变化值
i: 0 1 2 3 4 5 …… n
②列出内层语句得执行次数
内层循环语 ▲ ▲
句执行次数 ▲ ▲
(2次) ▲
▲
(4次)
③求和,写结果
那么执行次数之和就是
时间复杂度就是





Asymptotic notations 渐近符号
-
规则1:在表示算法运行时间的增长时,只保留主导项。
-
规则2:在表示算法运行时间的增长情况时,去掉常数系数。
Example.
1.
2.
3.
4.$ n^{3}$,
大O、大Ω和大Θ等渐近记号用于比较函数的极限行为:

- O (Big-O / 大O):渐近上界
含义: 提供了函数增长率的上限 (asymptotic upper bound)。通俗地说,它表示算法的运行时间增长得不会比
举例:
- 一个运行时间为
- 但它也是
总结: O 描述的是“最坏情况”(小于等于)。
-
含义: 提供了函数增长率的下限 (asymptotic lower bound) 。通俗地说,它表示算法的运行时间增长得不会比
举例:
-
一个运行时间为
-
但它也是
总结:
-
含义: 提供了函数增长率的精确描述,也称为“紧密界限”。当一个函数
举例:
-
-
总结:
关键区别
它是
它是
它是
它是
One can categorise the growth rate functions into a number of classes, which form a chain under the dominance relation:
$ 1<log n<(log n)^{2}<n<n log n<n^{2}<n^{2} log n<n^{3}<\cdots<2^{n}<n!$
Divide and Conquer 分治算法
卡拉苏巴算法与二分查找
- 分治法(divide-and-conquer technique)通过将计算问题分解为一个或多个规模更小的子问题,递归地解决每个子问题,然后将这些子问题的解合并起来,从而得到原问题的解。
- 通用分治策略:如果是
运行时间分析:提出一个递归关系

示例1:卡拉苏巴算法
给定两个输入数字x、y:如果x、y的长度均为1,则直接将x、y相乘;否则,将x和y各自分成两个数字,并得到3个大小为

示例2:二分查找 Binary Search
问题:从一个已排序的数字序列中查找一个数字。
函数二分查找(arr, 目标值, 起始索引, 结束索引)
输入:整数数组arr、索引start、end、整数target
输出:若目标值在arr中则返回“是”;否则返回“否”
如果起始索引 > 结束索引,则返回“该元素不属于此序列”
中间索引 ←⌈(起始索引 + 结束索引)/2⌉
如果arr[中间索引] = 目标值,则返回“找到该元素”
否则如果目标值 < arr[中间索引],则返回二分查找(arr, 目标值, 起始索引, 中间索引 −1)
否则返回二分查找(arr, 目标值, 中间索引 + 1, 结束索引)

1 | function BinarySearch(arr,target,start,end) |
时间复杂度:
- 分治法的时间复杂度分析:主定理Master Theorem——Three Cases
主定理提供了一种直接求解如下形式递归关系的方法
主定理允许我们通过比较函数
Case 1:
Case 2:
Case 3:


Example 1: Karatsuba’s Algorithm

Example 2: Binary Search
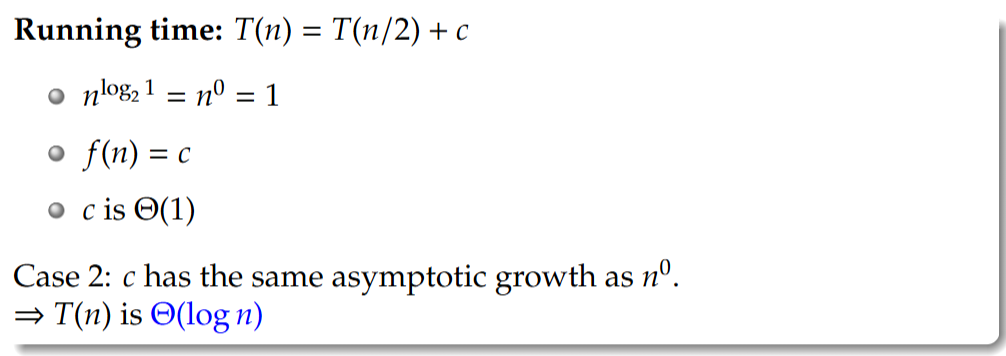
Matrix multiplication and Strassen’s algorithm 矩阵乘法与施特拉森算法
利用行列相同的矩阵可以分块相加这个规律进行分治法的计算,利用分组的思想进行改进。
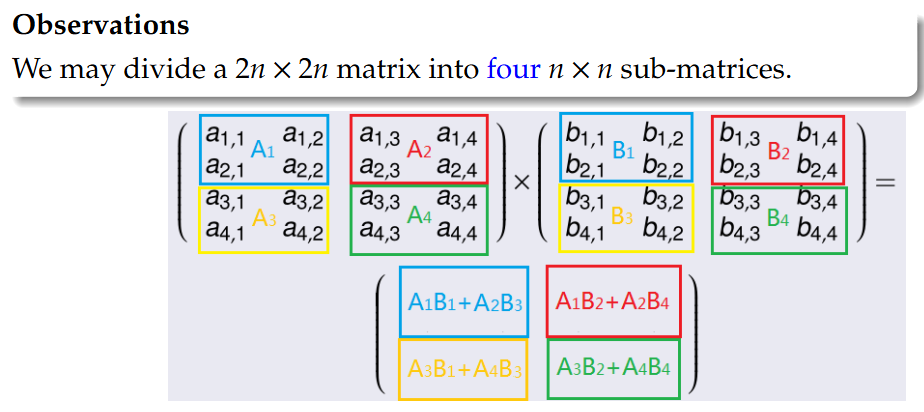



合并: 加上若干次矩阵加法(时间为
这个 Θ(n2) (或 cn2) 的复杂度是由矩阵加法(或减法)本身的性质决定的**。
简单来说:要将两个 *n*×*n* 的矩阵相加必须计算 *n*2 个新元素,因此您至少需要执行 *n*2 次加法运算。
- 什么是矩阵加法?
- 假设您有两个 n×n 的矩阵 A 和 B,您想计算它们的和 C=A+B。
- 矩阵加法的定义是逐个元素相加 (element-wise)。
- 也就是说,结果矩阵 C 中第 i 行第 j 列的元素 Cij,等于 A 矩阵的 Aij 加上 B 矩阵的 B**ij。
- 即:Cij=Aij+B**ij
- 总共有多少个元素?
- 一个 n×n 的矩阵(即 n 行 n 列)总共有 n×n=n2 个元素。
- 总共需要多少次运算?
- 为了计算出 C 矩阵,您必须为 C 中的每一个元素执行一次加法运算。
- 因为 C 矩阵有 n2 个元素,所以您总共需要执行 *n*2 次加法操作。
- 矩阵减法同理。
- 为什么是$ Θ(n^2)$?
- 算法分析中的 Θ (Theta) 符号表示一个“紧密界限”。
- 当我们说一个操作的时间复杂度是 Θ(n2) 时,我们的意思是它需要的时间既不多于 n2 的某个常数倍(即 O(n2)),也不少于 n2 的某个常数倍(即 Ω(n2))。
- 由于您必须执行 n2 次加法(不多也不少),所以这个操作的时间复杂度被精确地描述为 Θ(n2)。
Analysis of sorting algorithms排序算法分析
问题定义
排序问题旨在将一组键(例如整数、字符串)组成的列表(即数组或链表)进行排列,使每对相邻的键都处于指定的顺序中。
[输入] 一组(未排序的)键
[输出] 一个包含相同元素集
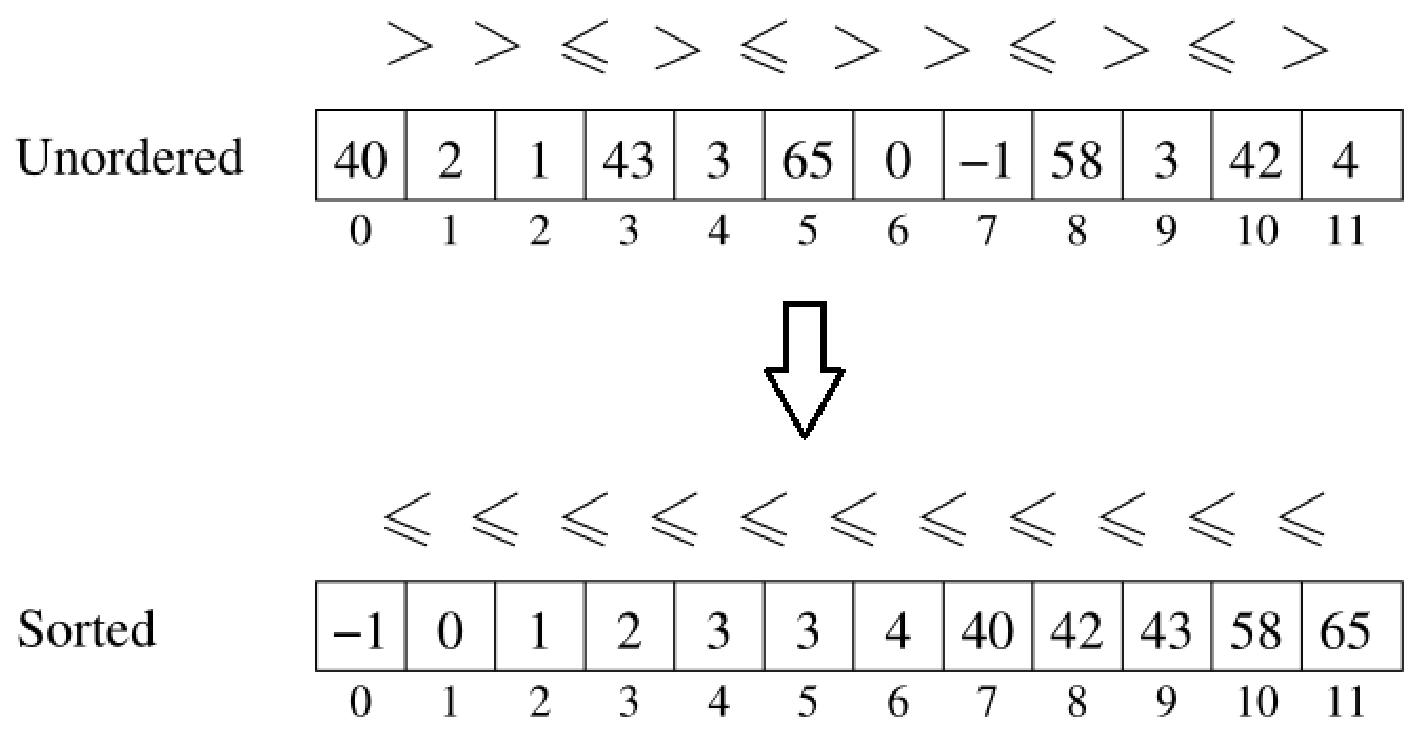
Algorithm 1: Selection Sort 选择排序
(1)将输入列表分割为已排序子列表和未排序子列表。
(2)排序子列表最初为空,未排序子列表则是整个列表。
(3)通过顺序扫描找到未排序部分的最大元素。
(4)将最大元素移至已排序部分的头部。
(5)如果未排序子列表为空,则终止;否则转到(3)。
例题:对数组 [43, 83, 0, 71, 91, 99, 15] 进行排序。
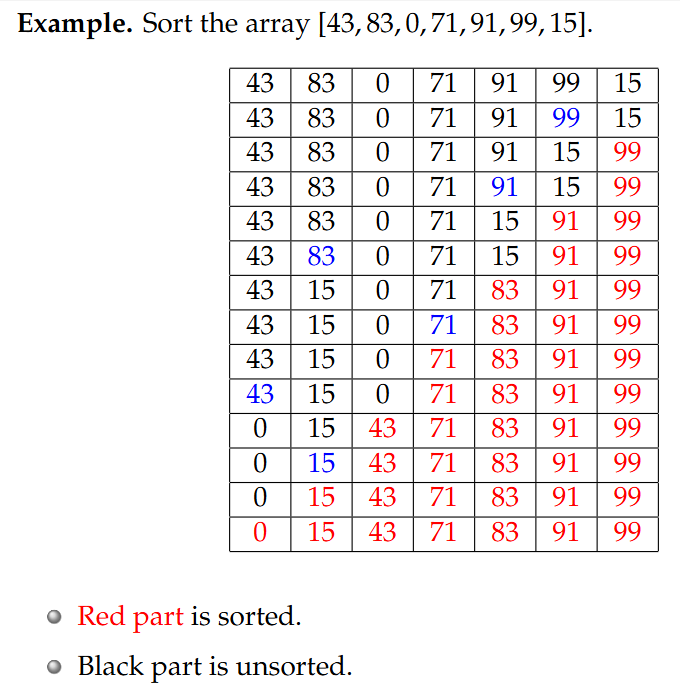
pseudo-code: Selection Sort Algorithm
1 | function SelectionSort(a[0...n-1]) |
pseudo-code: findmx function
1 | function findmax(a[0...l]) |
findmax会遍历整个未排序部分(设置$$i=0 . . \ell$$),findmax的每一步都会将a[max]与
时间复杂度分析
1.Comparison-based Sorting Algorithm基于比较的排序算法
如果一种排序算法仅使用顺序关系来比较键,则它是基于比较的,即我们通过回答“is $$x<y ?^{\prime \prime}$$”这类问题来确定元素的顺序。
例如: 选择排序是一种基于比较的排序算法:比较操作在findmax中进行。非比较排序算法包括桶排序(bucket sort)、基数排序( radix
sort)等(超出本课程的范围)。
基于比较的排序中的重要操作:
比较:
交换:3次变量更新。运行时间为
问题:选择排序算法的运行时间是多少?

找到$$a[0 . . \ell]$$的最大值需要
比较次数:
交换次数:最多 n-1 次
最坏情况下的运行时间:
Algorithm 2: Merge Sort 归并排序
归并排序是一种基于比较的算法,它运用分治法的思想(the idea of divide-and-conquer)来解决排序问题:
(1)要对输入列表进行排序,可将其拆分为两个子列表(split it into two sublists);
(2)递归地(recursively)对每个子列表进行排序;
(3)然后合并已排序的子列表,以对原始列表进行排序。
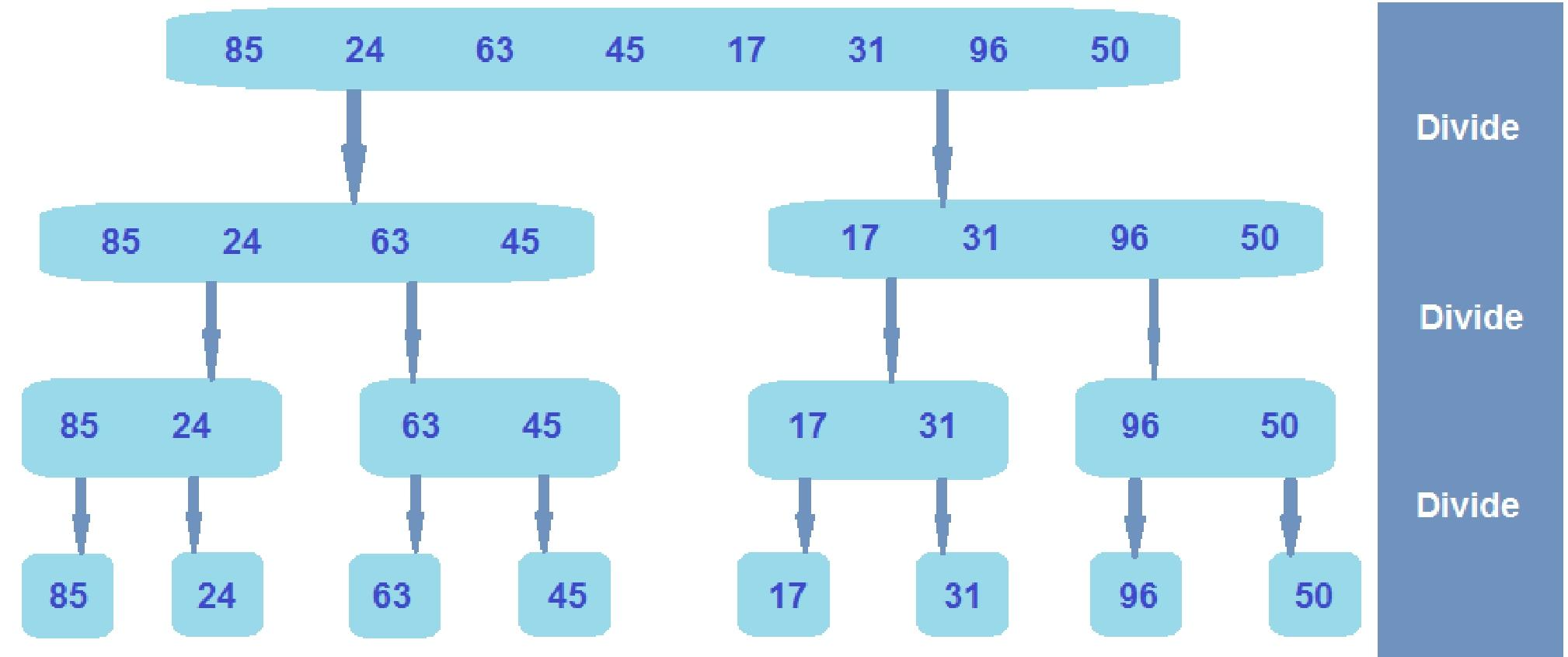
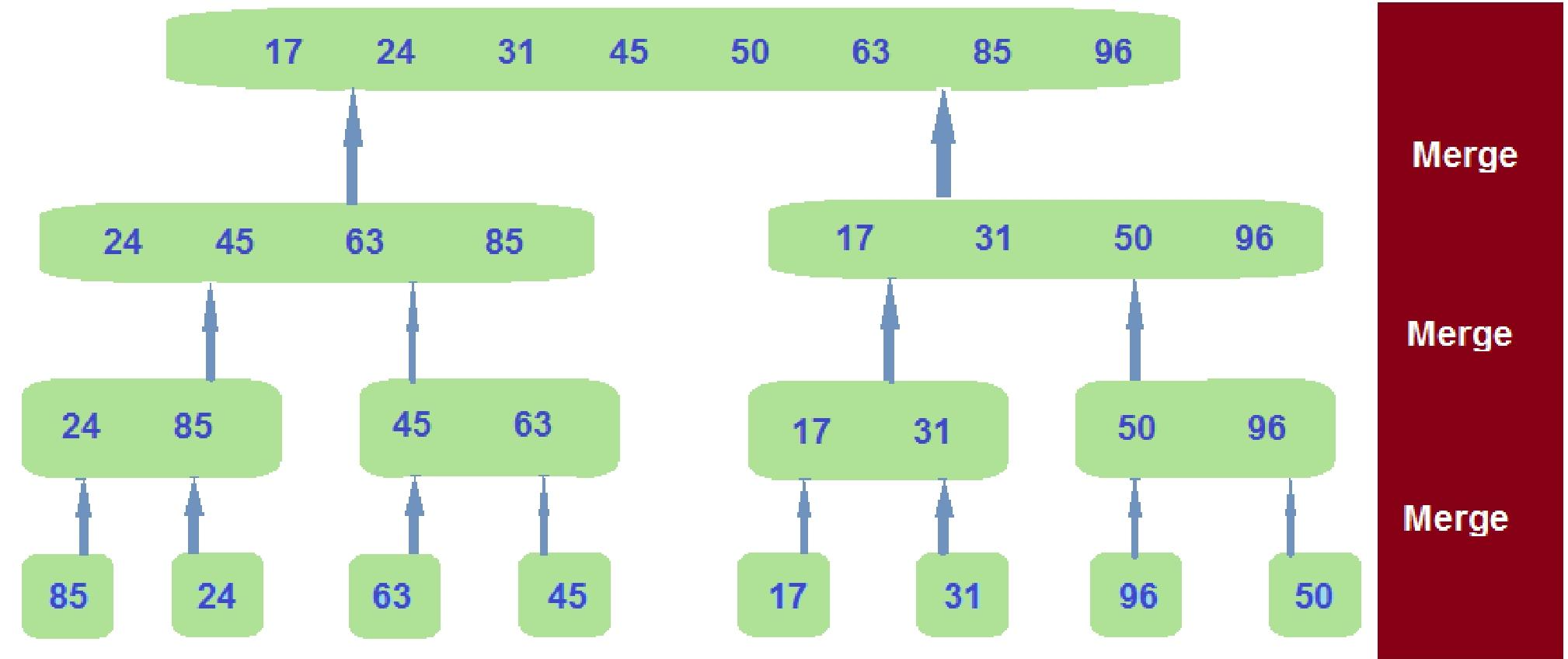
pseudo-code: Mergsort Algorithm
1 | function MergeSort(list input[0...n-1]) |
pseudo-code: The merge operation
1 | function Merge(list l[0...s],r[0...t]) |
问题:如何高效地执行合并操作?(跟yxc那个一样就是用i++,j++,k++的形式不停挪指针然后添加到一个新的列表里面就可以)
(1)为每个子列表创建一个指针。
(2)创建一个合并列表,并为该列表设置第三个指针。
(3)将指针置于每个列表的起始位置。比较所指向的元素,选择较小的那个作为排序列表的起始元素。然后移动该指针。
(4)迭代,直到一个指针到达其列表的末尾。
(5)将另一个列表的剩余元素复制到最终排序列表的末尾。
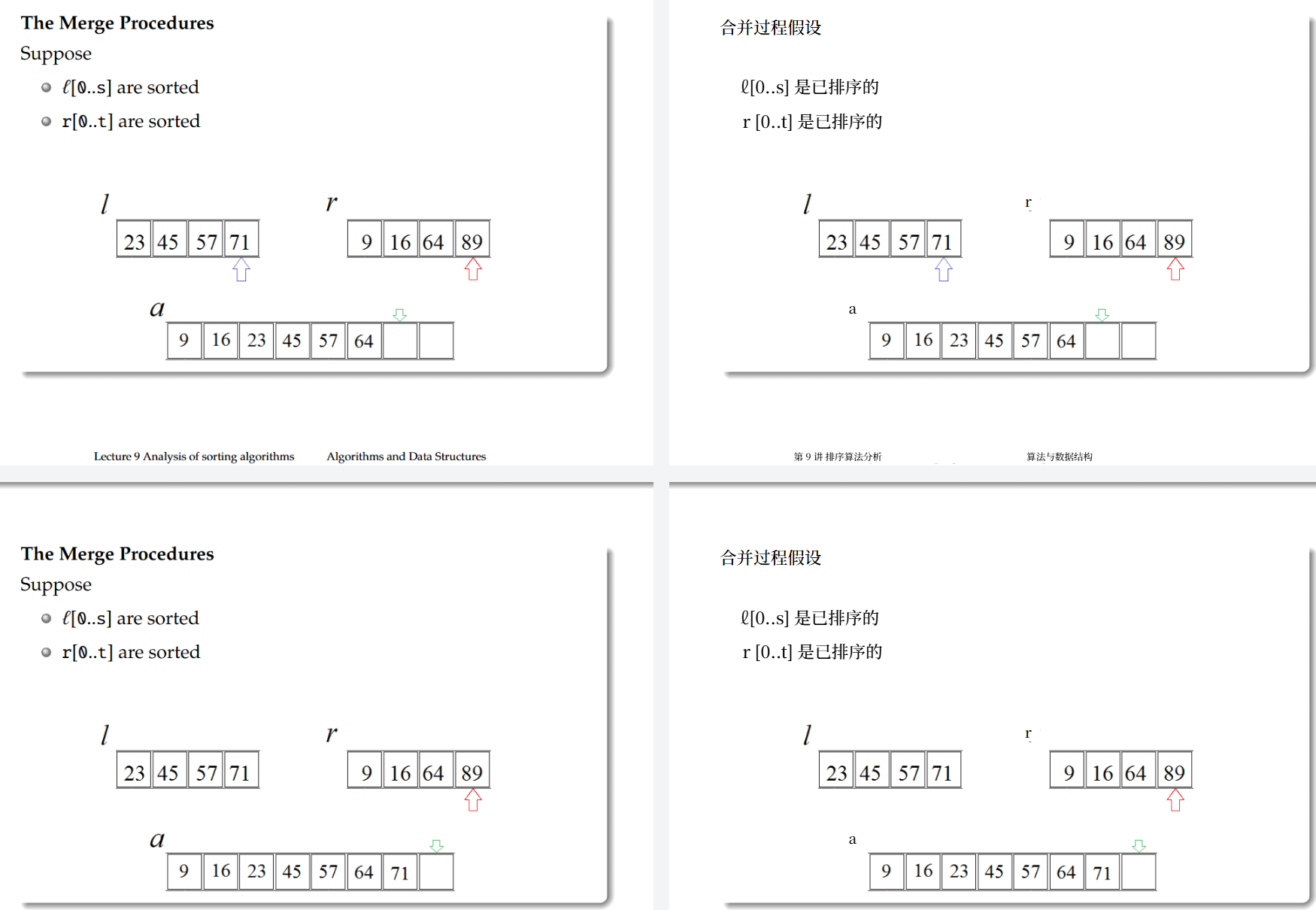
1 | function Merge(list l[0...s],r[0...t]) |
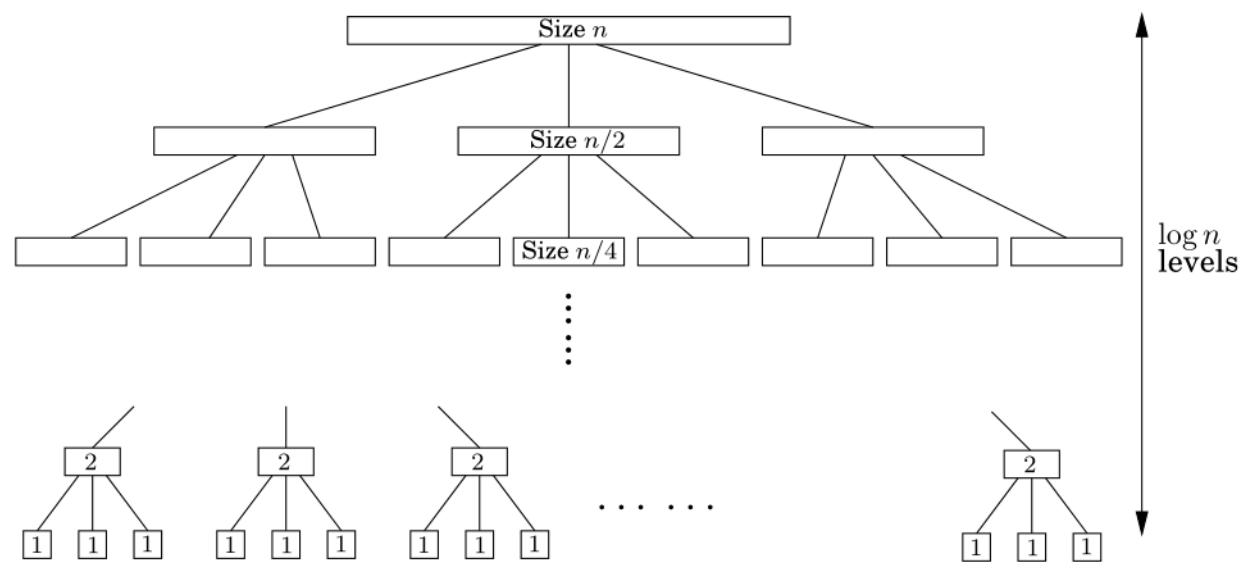
归并排序递归式(Mergesort recurrence):设T(n)表示对n个元素的列表进行归并排序的运行时间。那么当n>1且n是2的幂,
应用主定理,归并排序的运行时间为
归并排序是最高效的排序算法吗?任何排序算法的最短运行时间必须是多少?
任何基于比较的排序算法的最佳时间复杂度是
归并排序和快速排序的异同
(1)同:两者都是分治算法
①将输入列表拆分为两个子列表(Split the input list into two sublists)
②递归地对每个子列表进行排序(Recursively sort each sublists)
③合并已排序的子列表(Combine the sorted sublists)
(2)异
①MergeSort归并排序:分割非常简单(Splitting is very easy),比较是在合并过程中进行的(The comparisons are done during combining)
②QuickSort快速排序:比较是在分割过程中进行的(The comparisons are done during splitting),合并非常简单(Combining is very easy)
Algorithm 3: QuickSort 快速排序
(1)选择一个基准元素,并将列表划分为两个子列表:
①左侧子列表包含小于等于基准值的元素。
②右侧子列表包含大于基准值的元素。
(2)递归地对左右子列表进行排序
(3)合并已排序的子列表
例题:对数组 [4, 2, 3, 5, 1, 6] 进行快速排序。
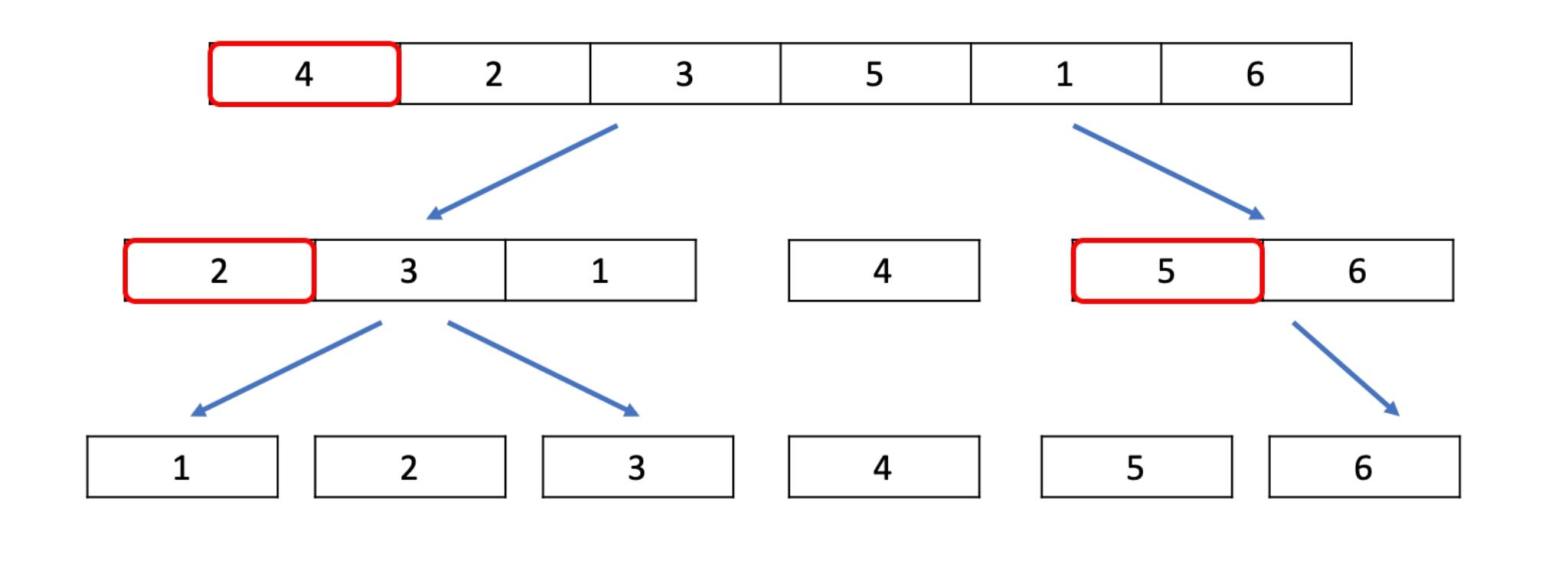
pseudo-code: QuickSort - basic
1 | function QuickSort(list a[0...n-1],integer i, integer j) |
pseudo-code: Linear time partitioning - Hoare’s method 线性时间划分——霍尔方法
给定一个列表L和L的一个基准值p,进行分区,使得L左侧的所有元素都是
(1)从列表两端的指针开始。当指针交叉时停止
(2)在每一步,递增左指针,直到我们遇到一个大于p的元素;将右指针递减,直到遇到小于等于p的元素。
(3)交换这些元素并继续。当指针交叉时,将右指针与基准值交换。
1 | function Partition(list a[0...n-1],integer i,integer j) |
问题:快速排序算法的运行时间是多少?
设

时间复杂度为
Graph Traversal 图的遍历
Lecture 10 图的概述
1.图是一个对G=(V, E),其中V是有限的节点(或顶点)nodes (or vertices) 集,E是G中被称为边(edges)的不同顶点的(可能为空的)无序对(unordered pairs)集合。
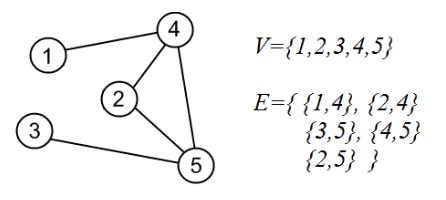
①不允许两个顶点之间存在多条边。
②不允许自环,即E是一个反自反关系。
③每条边都是双向的,即E是一个对称关系。
2.有向图(directed graph)(或简称为digraph)是一个对G=(V, E),其中V是顶点(或节点)的有限集,且
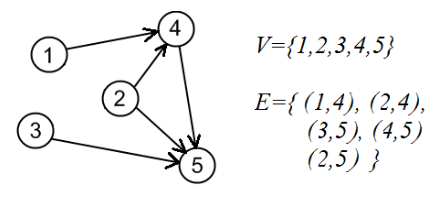
3.多重图(Multigraphs):G=(V, E),其中
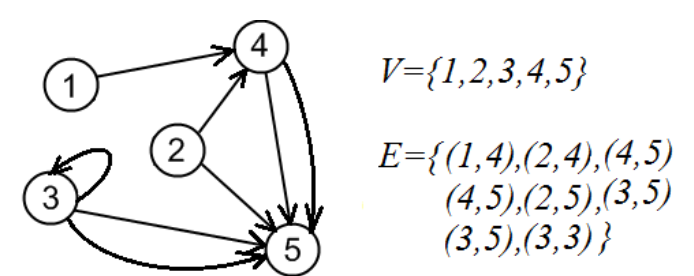
4.加权(有向)图(Weighted (di)graphs):G=(V, E, f, D),其中(V, E)是一个(有向)图,
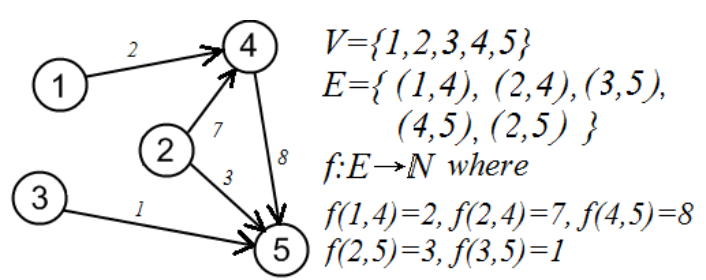
5.让G=(V, E)是一个图。
①图G的阶数(order)是指G中节点的数量,即
②通常用字母
③如果
④如果

6.术语(Terminology)
(1)对于(无向)图((undirected) graph):
①顶点的度(The degree of a vertex)是其相邻顶点的数量。
②通路(walk)是顶点的序列,其中每对连续的顶点(consecutive pair of vertices)由一条边连接。
③路径(path)是指顶点不重复的通路(walk)。
(2)对于有向图(directed graph):
①节点的入度是指该节点的入边邻居数量。(The in-degree of a node is the number of incoming neighbours of the node.)
②节点的出度是指该节点的外向邻居数量。(The out-degree of a node is the number of outgoing neighbours of the node.)
③一条(有向)路径是节点的序列,其中每对连续节点都由一条有向边连接。(A (directed) walk is a sequence of nodes where each consecutive pair of nodes are connected by a directed edge.)
④一条(有向)路径是指其中没有节点重复的一条通路。(A (directed) path is a walk in which no node is repeated.)
(3)特殊图类型:
①(完全图Complete graphs)如果所有不同节点对在图G中都是相邻的,则该图是完全图。具有n个节点的完全图用
②(路径图Path graphs)路径图是G=(V, E),其中
③(循环图Cycle graphs)循环图是一种图G=(V, E),其中
④(轮图Wheel graphs)轮图是一个图G=(V, E),其中
这个轮图用
7.状态转移图(Transition Diagrams)
一个(软件/硬件)系统可以用一组状态来正式表示。系统的运行涉及状态之间的转换。状态转换图是一种有向图,它表示系统的状态以及状态之间的转换。目标是验证系统是否满足某些重要特性:①某些状态永远不会达到。②某些状态会被重复访问。形式化验证领域(formal verification)研究的是验证此类性质是否得到满足的方法。
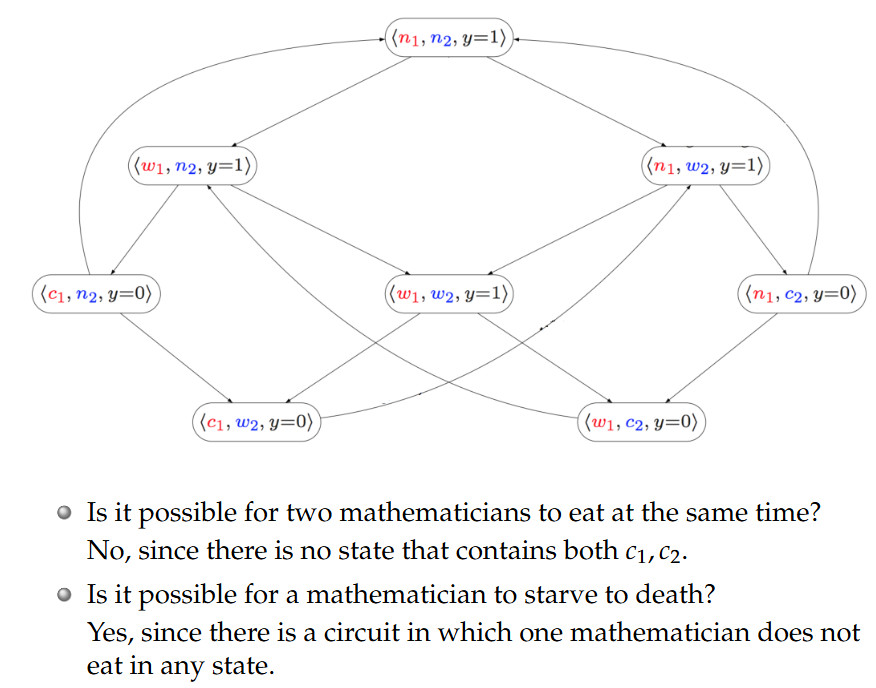
8.图的表示:邻接矩阵(Adjacency matrix)和邻接表(Adjacency list)
在分析图操作时,我们根据图的阶数n和大小m(order n and size m)来衡量其复杂度。
(1)邻接矩阵(Adjacency matrix)
假设G是一个有向图,其节点为
G的邻接矩阵是
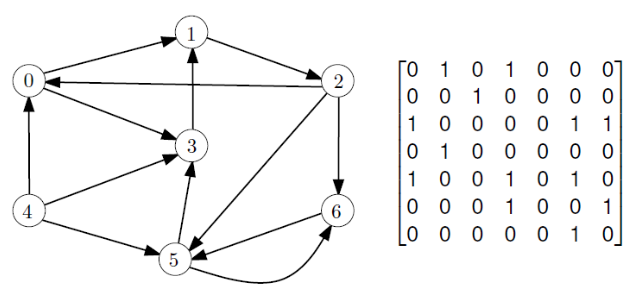
(2)邻接表(Adjacency list)
假设G是一个有向图,其节点为
有向图G的邻接表是n个列表组成的列表,
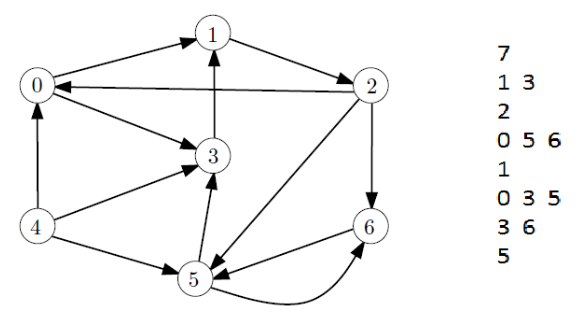

Basic definition: graph, digraph, multigraph, weighted graph基本定义:图、有向图、多重图、带权图
Basic terminology: size, order, adjacency, neighbourhood, degree基本术语:大小、阶数、邻接、邻域、度
Basic graph types: complete graphs, cycles, etc.基本图类型:完全图、环等。
Graphs as models for: network topology, transitions, etc.作为模型的图:网络拓扑、转换等。
Graph representations: adjacency matrix, adjacency list图的表示:邻接矩阵、邻接表
Lecture 11 Depth First Search 深度优先搜索
1.Depth First Search: Recursive Implementation递归实现
1 | Algorithm dfs |
1 | Algorithm explore(G,v) |
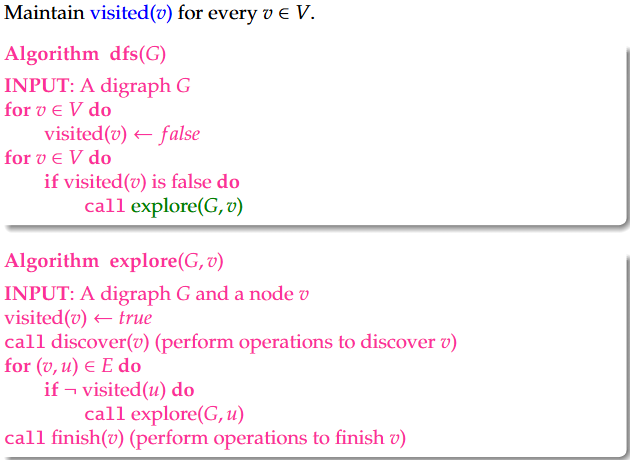
2.Depth First Search: Stack Implementation
Note: The current path changes in a FILO order.
1 | Algorithm explore_stack(G, v) |

3.时间复杂度分析
发现并完成每个节点:O(n)
访问每个节点的出邻节点:O(n+m)(使用邻接表);O(n^{2})(使用邻接矩阵)
DFS算法使用邻接表的时间为O(n+m),使用邻接矩阵的时间为O(n^{2})。
4.可达性(Reachability)
我们说,在图G中,如果存在一条从节点v出发并终止于节点u的路径,那么节点u是从节点v可达的(reachable)。
也就是说,假设我们对输入图G和图G中的节点v运行explore(G, v),那么算法访问的任何节点u当且仅当它是从v可达的。
- 如果u被访问过,那么u是可达的。这是因为深度优先搜索(DFS)只沿着图G中的边进行遍历。
- 如果u是可达的,那么u会被访问到。
5.搜索森林(Search Forest)
深度优先搜索(DFS)定义了一棵或多棵搜索树(search trees),在有向图中形成一个森林。这些树包含了深度优先搜索(DFS)用于访问图G中节点的所有路径。
在执行深度优先搜索(DFS)时,我们如何识别搜索树?
在算法中维护一个“计时器”,以及每个节点u的两个时间pre(u)和post(u):
pre(u):首次访问u的时间步。
post(u):u最后被访问的时间步。
写下一个符号序列(n和n),其中
如果
如果
注意:u)不是说返回的时候经过这里而是说彻底离开这个节点了,也就是说如果这个节点还是其他路径的开始那么就不可以有u)
这个就跟操作系统中的PV操作似的有始就有终,有P就有V
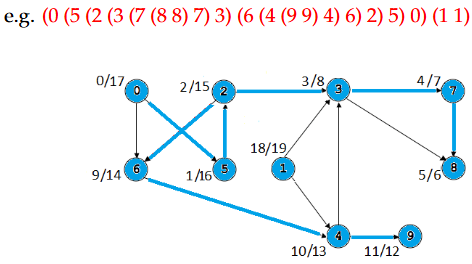
Lecture 13 Directed Acyclic Graph有向无环图
1.定义:A directed acyclic graph (dag) is a digraph that does not contain a cycle.有向无环图(dag)是不包含环的有向图。
2.设T为G中的深度优先搜索(DFS)森林。G中有四种类型的边:
①If(u, v)belongs to the search forest, (u, v)is a tree edge. 如果(u, v)属于搜索森林,那么(u, v)就是一条树边。
②否则,如果u是T中v的祖先,则(u, v)是一条前向边forward edge
③否则,如果v是T中u的祖先,则(u, v)是一条回边back edge
④否则,(u, v)是一条交叉边cross edge
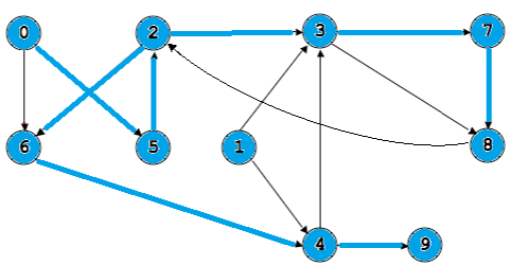
Tree edges: (0,5)(5,2),(2,6),(2,3),(3,7),(7,8),(6,4),(4,9)
Forward edges: (0,6),(3,8)
Back edges: (8,2)
Cross edges: (4,3),(1,3),(1,4)
3.设G为有向图。则以下表述等价:
①G是一个有向无环图DAG
②深度优先搜索森林没有回边
4.以下算法的运行时间为
1 | Algorithm: acyclic(G) |
5.DFS and Linearisations深度优先搜索与线性化
有向图G的线性化(或拓扑排序)是G中所有节点的列表,使得如果G包含边(u, v),那么u会出现在列表中v的前面。
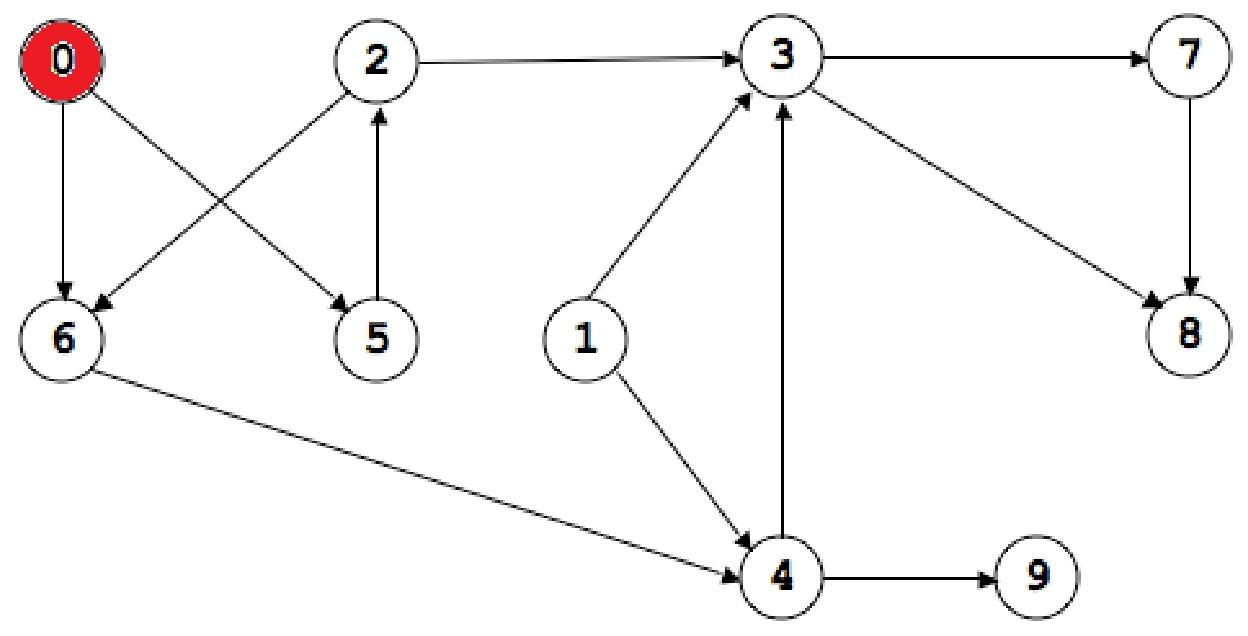
Topological Sorts:
0,5,2,6,1,4,3,7,9,8; 1,0,5,2,6,4,9,3,7,8
问题1. 是否存在无法线性化的有向图?答案:是的!带有环的有向图。
问题2:哪些有向无环图可以线性化?答案:所有的有向无环图都可以!我们现在要介绍用于将有向无环图线性化的算法。
6.线性化算法1:Zero In-degree Algorithm零入度算法
零入度算法为有向无环图找到一种线性化方式:

1 | Algorithm: ZeroInDegree(G) |
Running time: The algorithm runs in time O((n+m) n).
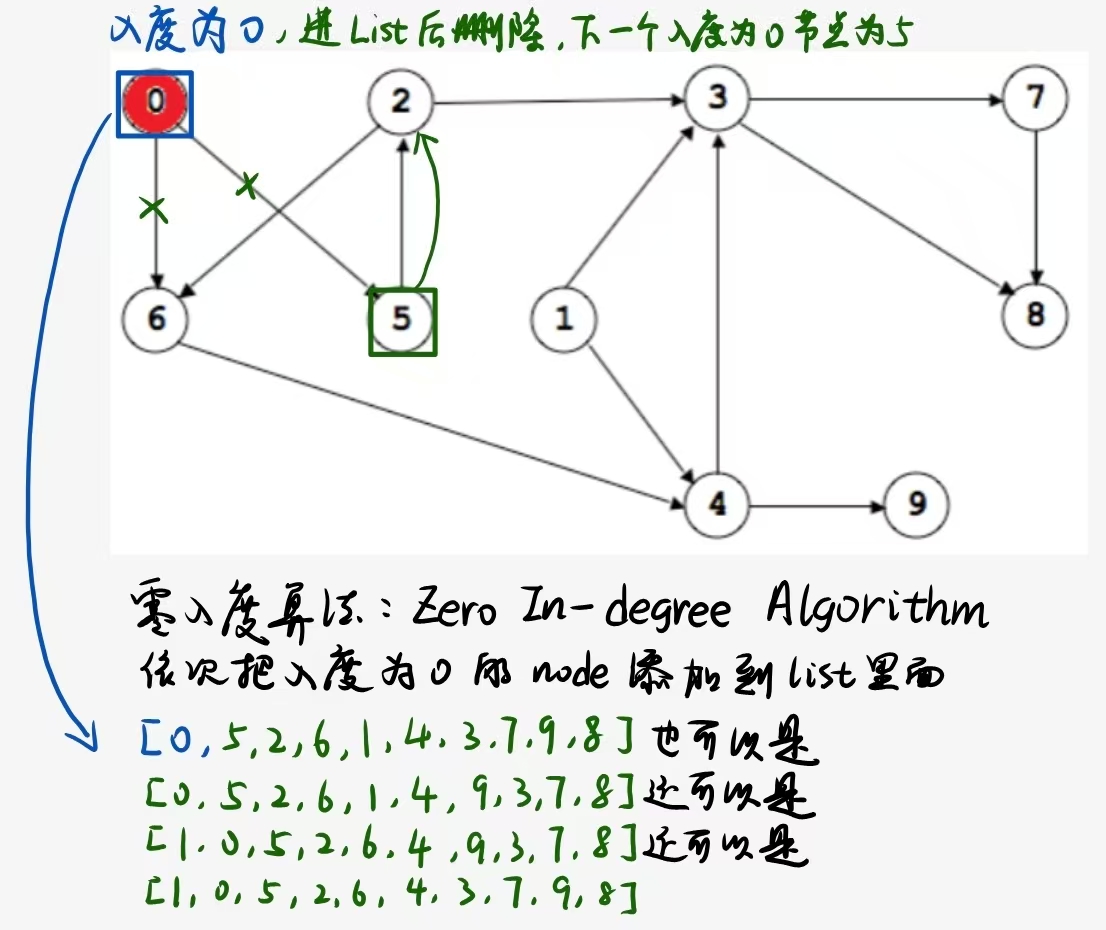
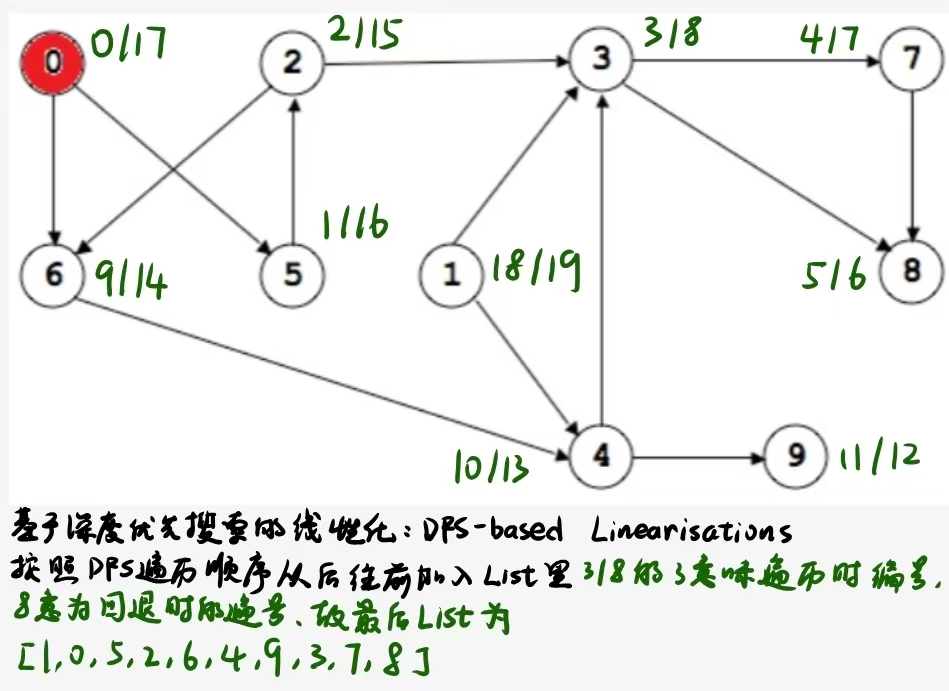
7.线性化算法2:DFS-based Linearisations基于深度优先搜索的线性化

1 | Algorithm: DFS-Linearise(G) |
We obtain an easy algorithm for graph linearisation in time O(m+n) : Output the list of nodes in decreasing finishing order.
9.总结
①Directed acyclic graph (DAG)有向无环图(DAG)
②Acyclicity problem: DFS-based algorithm (no back edge)无环性问题:基于深度优先搜索的算法(无回边)
③Linearisation problem线性化问题:
Zero in-degree algorithm: O(n(m+n))零入度算法:O(n(m+n));DFS-based algorithm (decreasing finishing order): O(m+n)基于深度优先搜索(DFS)的算法(按完成时间降序排列):O(m+n)
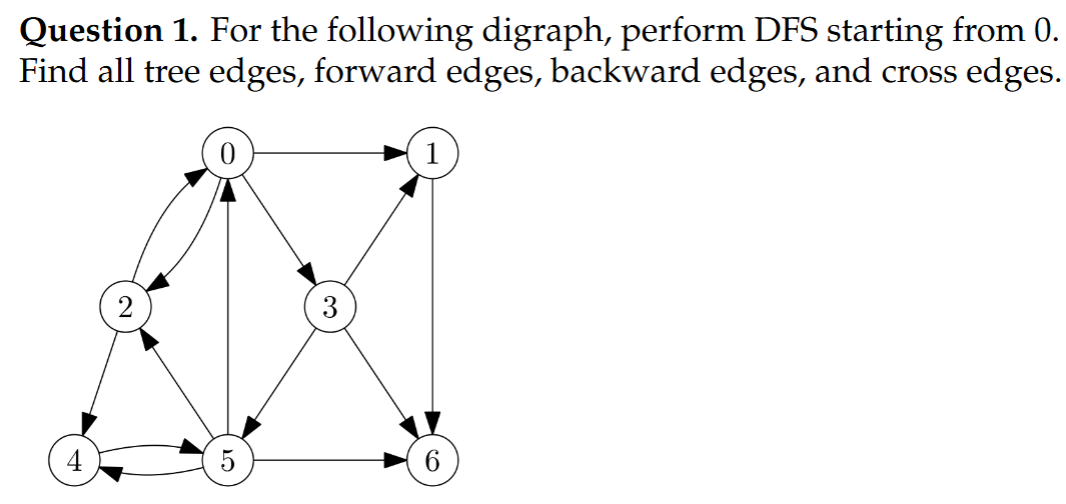
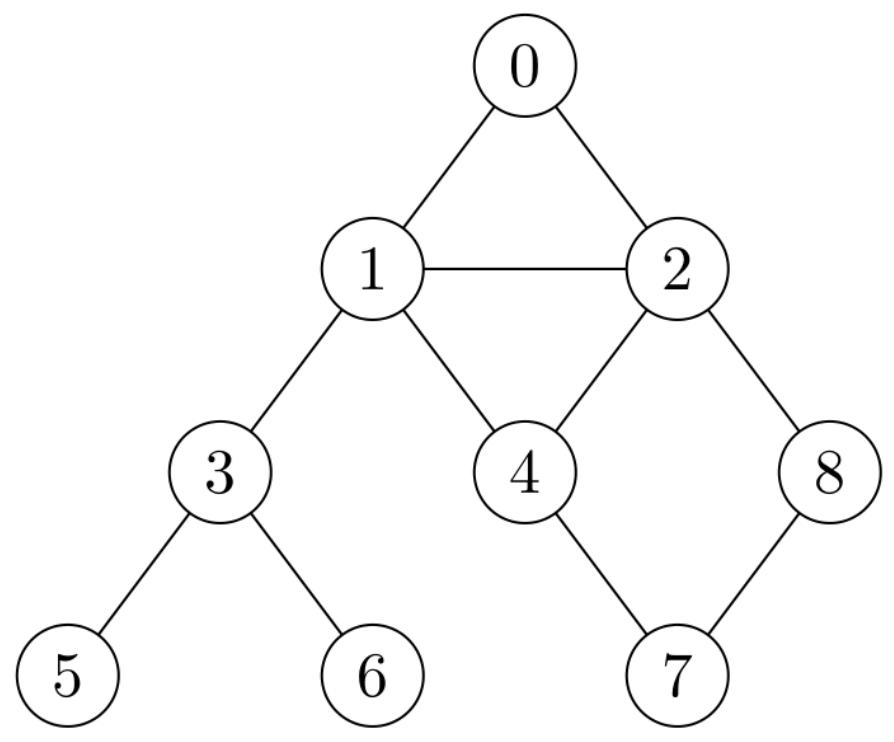
假设按照结点的编号从小到大遍历
Tree edges: 构成DFS森林骨架的边(0,1)(0,2)(2,4)(4,5)(5,6)(0,3)
Forward edges: 从祖先指向后代,但不是树边的边: None
Back edges: 指向已在当前递归栈中的祖先节点的边(2,0)(5,4)(5,2)(5,0)
Cross edges: 指向已经处理完成的节点(通常是跨分支)(3,5)(3,1)(3,6)(1,6)
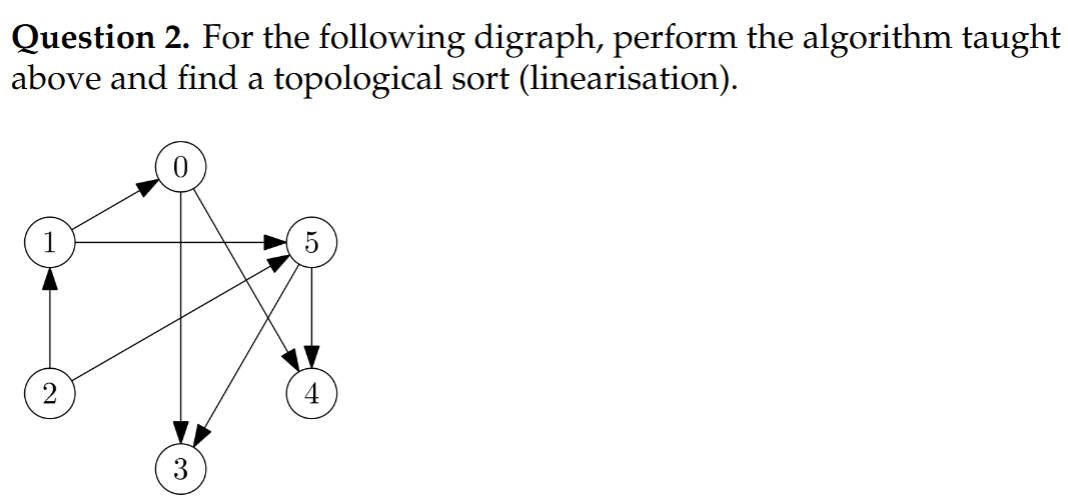
2,1,0,5,3,4/2,1,0,5,4,3都可以(用零入度算法,感觉用dfs-based容易错)
Lecture 14 Connectivity and Components连通性与组件
1.为什么要分解图?
[分治法] 通常,当我们解决图上的问题时,将图分解为多个组件,在各个组件上解决问题,然后合并解决方案会高效得多。
2.定义 [子图]:令
,其中
2.Decomposing Undirected Graphs无向图的分解
如果存在一条路径连接两个节点,那么一个节点是从另一个节点可达的。
我们可以将图分解为等价类(equivalence classes):如果两个节点可以相互到达,那么它们属于同一类。每个等价类都是一个连通分量(connected component)
3.Undirected Connectivity无向连通性
A connected components is the induced subgraph of a maximal set of nodes that are pairwise reachable.连通分量是由最大节点集所诱导出的子图,其中这些节点两两之间均可到达。
如果一个无向图只包含一个连通分量,那么它就是连通的。
我们可以使用深度优先搜索(DFS)来判断两个节点是否在同一个连通分量(CC)中。
运行时间:O(m+n)
4.Decomposing Directed Graph有向图分解
有向连通性:在有向图G中,如果存在从节点u到v的路径以及从v到u的路径,我们就称两个节点u、v处于同一个强连通分量(SCC)中。如果一个有向图只包含一个强连通分量,那么它就是强连通的。
极端特殊情况:
①如果G是无环的(acyclic),那么每个节点自身就是一个强连通分量。因此,图G中有n个强连通分量。
②如果G是一个环(cycle),那么G是一个强连通分量。因此,图G中只有1个强连通分量。
③如果G是无向的(undirected),那么当u可以到达v时,u和v就在同一个强连通分量中。因此, checking SCC is same as reachability检查强连通分量与检查可达性是相同的。
- SCC问题:输入:一个有向图G => 输出:G的所有强连通分量
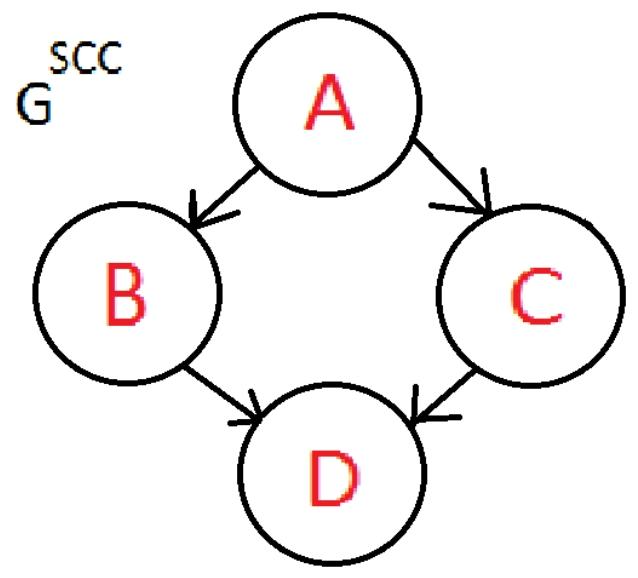
5.Meta-Graph元图
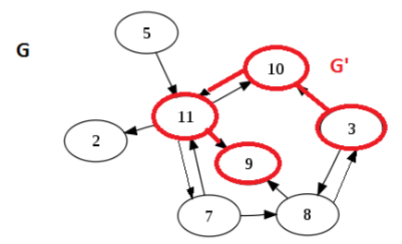
给定一个图G。如果我们将同一强连通分量(SCCs)中的所有节点合并在一起,只保留不同分量之间的边,那么我们就得到了元图
源点与汇点(source and sink):A is a source, D is a sink.
6.求强连通分量算法

1 | Algorithm SCC(G) |
本质上,该算法运行两次深度优先搜索(DFS):第一次在G上,然后在
第二次,当无处可去时,按照第一次深度优先搜索的完成时间从大到小的顺序选择下一个节点。
通俗理解:
1.什么是 Meta-Graph?
你可以把有向图想象成若干个“小岛”。
- 岛内 (SCC):在一个岛内部,所有地点都是互通的(你可以从 A 到 B,也可以从 B 回 A)。
- 岛之间 (Meta-Graph):岛与岛之间可能只有单向桥。
- Meta-Graph 的性质:如果我们把每个“小岛”看作一个点,那么这些岛组成的图一定是没有环的(DAG)。因为如果岛 A 和岛 B 互相能到达,那它们其实就是同一个大岛。
2.我们的困境是什么——或者说,GCC问题是在解决什么?
我们要找出所有的“岛”。 这就好比你要去探测地图。最简单的策略是:找到一个“死胡同岛”(Sink,汇点)——也就是那种你可以进去,但绝对出不来的岛。 如果你能找到这样一个岛,进去把岛内所有点标记出来,然后把这个岛从地图上“切掉”,再去找下一个死胡同岛,就能把所有 SCC 找出来。
问题是: 在原图里,你很难直接一眼看出哪个是“死胡同岛”。
4.为什么要反转图 (
这时候算法的精髓来了:
- 第一遍 DFS(在原图 G 上):
- PPT 21-23 页告诉你:虽然我们找不到“死胡同岛”,但 DFS 有个特性——最后结束遍历 (Finished Last) 的那个点,一定属于“源头岛” (Source)(即水流流出的地方,只有路出去,没路从别的岛进来)。
- 这就尴尬了,我们要找的是“死胡同”,但 DFS 帮我们找到的是“源头”。
- 反转大法:
- 如果我们把图中所有箭头的方向反过来(求
- 结论:我们在原图
- 如果我们把图中所有箭头的方向反过来(求
4.这种题型最后输出的结果意味着什么?
输出结果 The Strongly Connected Components are
我们可以从以下三个维度来理解这个结果:
(1) 花括号
在这个花括号里的所有点,像是形成了一个“微信群”或者“环岛”。
-
- 你可以从
- 只要你在这个集合里,你就永远不会被“困死”,总能找到路回家。
- 你可以从
-
(2) 为什么是两个分开的集合,而不是一个大的
这是最关键的!这说明这两个圈子之间存在“生殖隔离”(单向通行)。
- 在原图中,有一条路可以从
- 但是!一旦你跨进了
- 这就是为什么它们必须被切分成两个独立的 SCC。如果它们能合体,必须要求
(3) 宏观视角:元图 (Meta-Graph)
PPT 第 15 页提到了 Meta-Graph。这个结果其实把复杂的 5 个点简化成了 2 个超级点(Super Nodes)。
如果把
- A (
- B (
- 我们之前的算法(反转图
总结:当你写下
“这张图由两个内部循环的系统组成。你可以从第一个系统单向去往第二个系统,但去了就回不来了。”
例题
通用解题步骤
① 第一遍 DFS(记录“完成时间”):
- 在原图
- 关键点:不看开始时间,只看结束时间。当一个节点的所有邻居都访问完了,该节点即将“回溯”结束时,把它压入栈 (Push to Stack)。
- 结果:你会得到一个装满节点的栈,栈顶是最后结束遍历的节点(通常是源头类的节点)。
② 构建转置图 (
- 把原图里所有边的方向反转(起点变终点,终点变起点)。
- 注意:节点位置不变,只变箭头方向。
③ 第二遍 DFS(输出 SCC):
- 按照①中栈的顺序(从栈顶弹出一个,处理一个),在转置图
- 如果弹出的节点没被访问过:以它为起点跑 DFS,能摸到的所有新节点,就构成一个强连通分量 (SCC)。
- 如果弹出的节点之前已经被访问过:直接跳过。
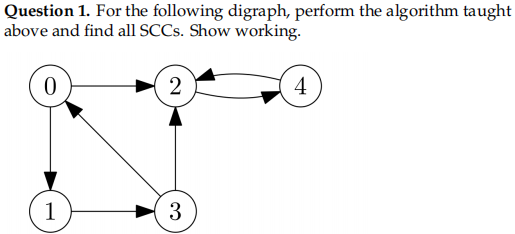
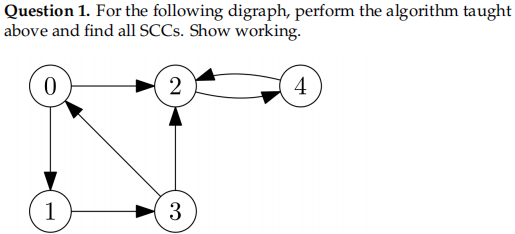
题目图示: 节点
原始边:
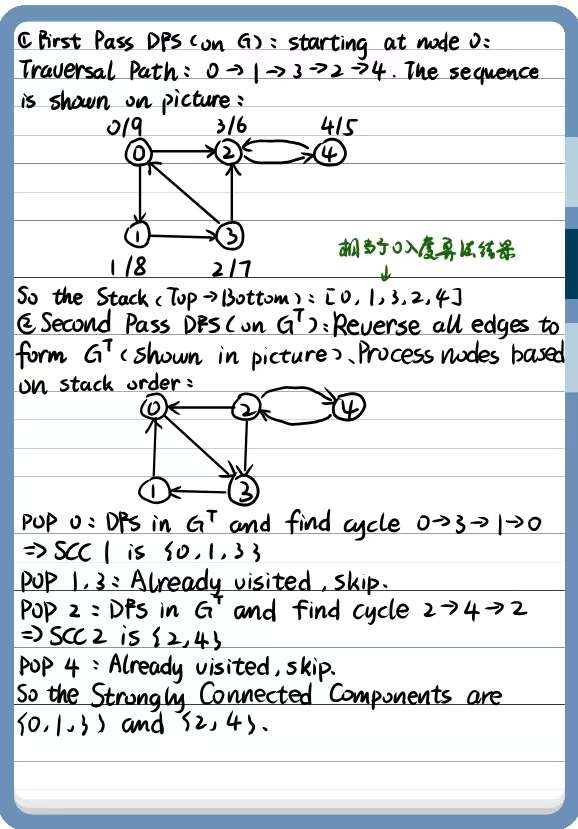
① 第一遍 DFS (Run DFS on G)
我们假设从节点 0 开始遍历(这是最常见的起点)。
- 访问 0
- 在节点 3:它可以去 0(已访问)或 2。我们选择去 2 (
- 在节点 2:去 4 (
- 在节点 4:只能去 2(已访问)。无路可走,4 完成。
- 回溯到 2:无路可走,2 完成。
- 回溯到 3:无路可走,3 完成。
- 回溯到 1:无路可走,1 完成。
- 回溯到 0:无路可走,0 完成。
- 此时栈的状态(从顶到底):
0, 1, 3, 2, 4。
② 构建转置图 (
将所有边反向:
-
-
-
-
-
-
-
③ 第二遍 DFS (DFS on
我们根据栈顶顺序依次取出节点:0, 1, 3, 2, 4。
- 弹出栈顶 0:
- 在
-
-
-
- (注意:在
- 结果:发现第一个 SCC
- 在
- 弹出 1:
- 节点 1 已经被刚才的 SCC 包含并标记为“已访问”,跳过。
- 弹出 3:
- 节点 3 已经被访问过,跳过。
- 弹出 2:
- 在
-
-
- (注意:2 还有边去 0 和 3,但 0 和 3 已经被归类到上一个 SCC 且移除了,所以不走)。
- 结果:发现第二个 SCC
- 在
- 弹出 4:
- 节点 4 已经被访问过,跳过。
最终答案 (Final Answer):
The Strongly Connected Components are
Lecture 15 Breadth First Search 广度优先搜索
1.引言:图遍历的用途(Uses for Graph Traversals)
①Searching (DFS)搜索(深度优先搜索)
②Reachability (DFS)可达性(深度优先搜索)
③Decomposing graphs (DFS)图分解(深度优先搜索)
④Calculating distances (DFS is not suitable)计算距离(深度优先搜索不适用)
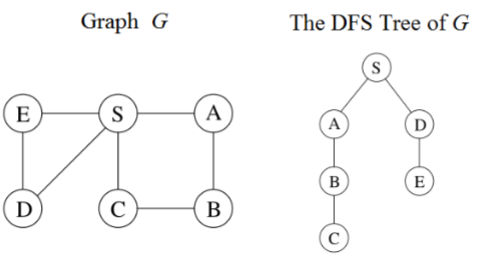
2.Distances Between Nodes节点间的距离
设G为一个图,路径的长度是路径中边(“步数”)的数量。节点u到,设为
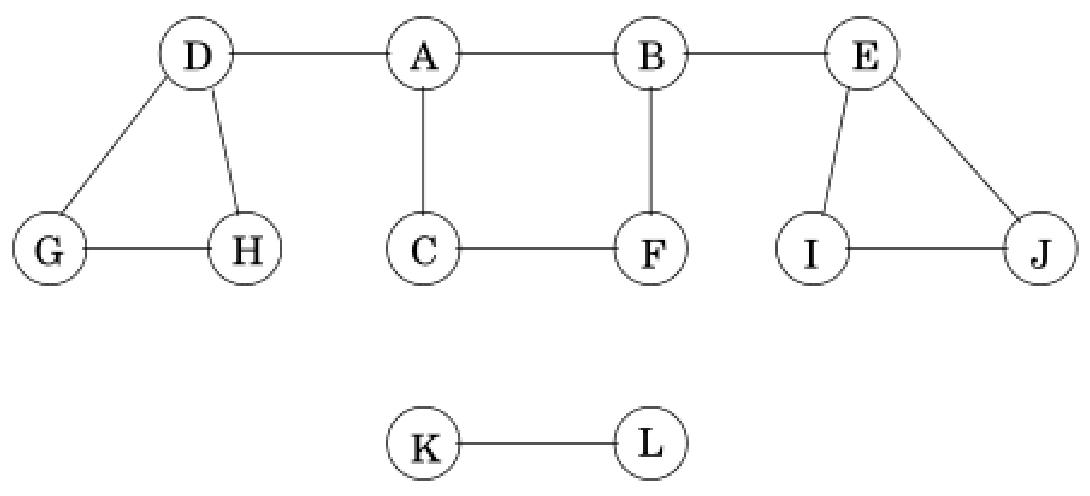
Distance between
Distance between
3.BFS旨在解决下面两个问题:
①距离问题
输入:一个图G,以及两个节点u、v
输出:u到v的距离
②最短路径问题
输入:一个图G,以及两个节点u、v
输出:从u到v的最短路径


4.BFS广度优先搜索的队列实现
维护一个待探索节点的队列。Maintain a queue of to-be-explored nodes.
在每次迭代中:
①首先处理队列中的第一个元素;出队。
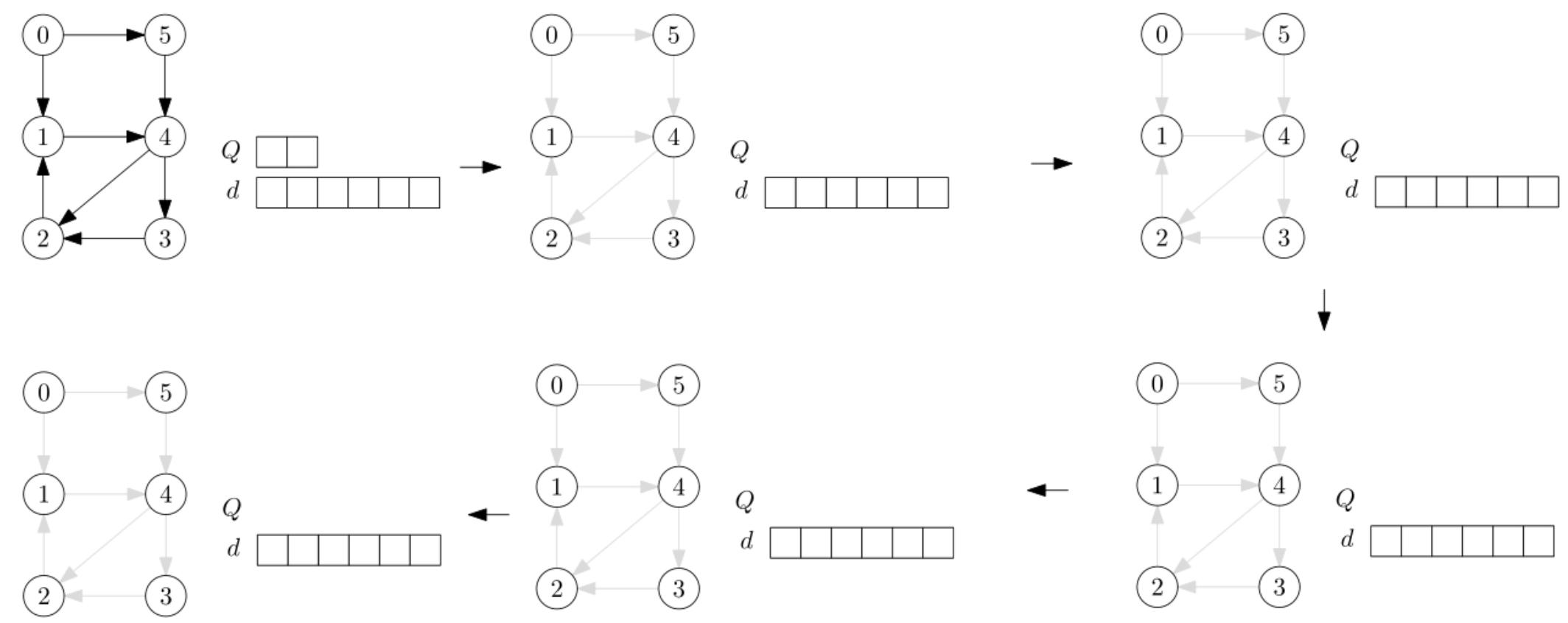
②然后将出队元素的出边邻居入队。
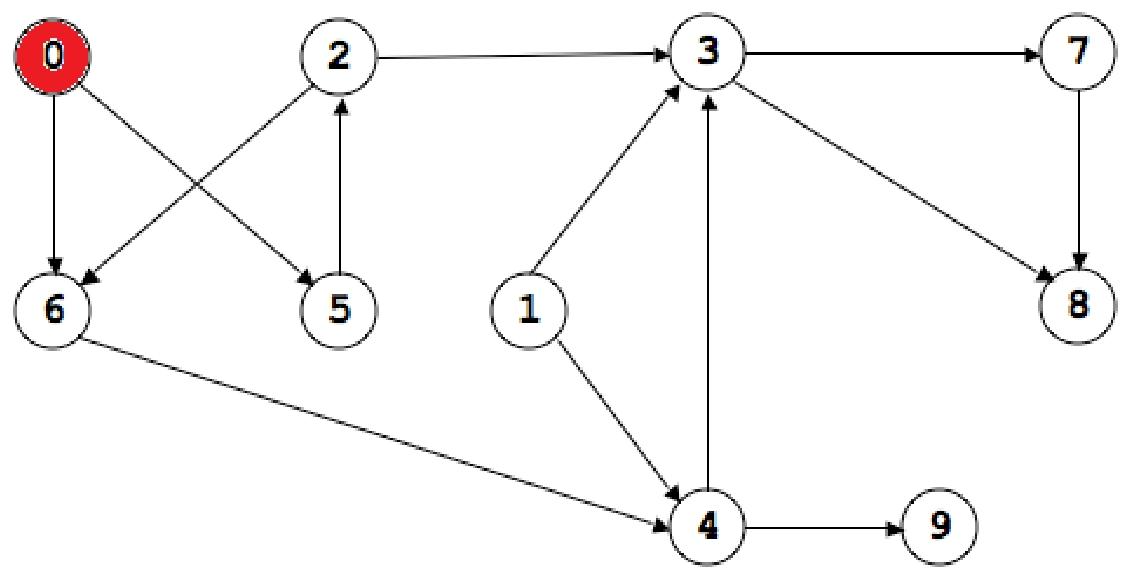
此时队列是[0];它的出边是5、6,因此退0进5、6->[5.6];5的下一个是2,因此退5进2->[6,2];6的下一个是4,因此退6进4->[2,4]……以此类推;到了后面走到[9,7,8]的时候已经没有路走了,就一个一个出队列,[9,7,8]->[7,8]->[8]->[],最后再把1加进来->[1];最后又变为空队列
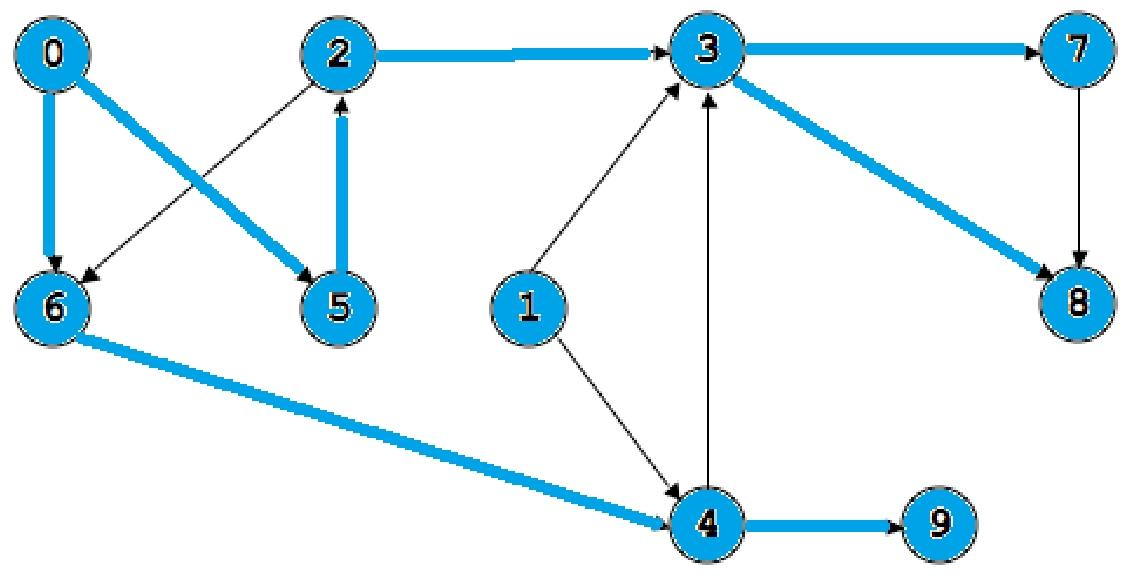
5.BFS伪代码
Maintain a field
Procedure
1 | INPUT: A graph G and a starting node s |
Procedure
1 | INPUT: A graph G and a starting node s |

6.时间复杂度分析
Every node u in G may be enqueued and dequeued at most once;G中的每个节点u最多可入队和出队一次
Every edge may be checked at most once;每条边最多可能被检查一次
因此,BFS算法的运行时间为
7.Summary: DFS versus BFS 深度优先搜索与广度优先搜索
(1)DFS深度优先搜索:该算法对图进行深入但范围狭窄的探索。
只有当没有新节点时才后退。
①实现:使用栈作为辅助数据结构。也可以通过递归实现。
②运行时间:
③应用:这可用于分析可达性、线性化和连通性。Applications: This could be used for analyzing reachability, linearizability, connectedness.
(2)BFS广度优先搜索:该算法对图进行浅层但广泛的探索。
按距离递增的顺序访问节点。
①实现:可以使用队列作为辅助数据结构。
②运行时间:
③应用:这可用于计算距离。
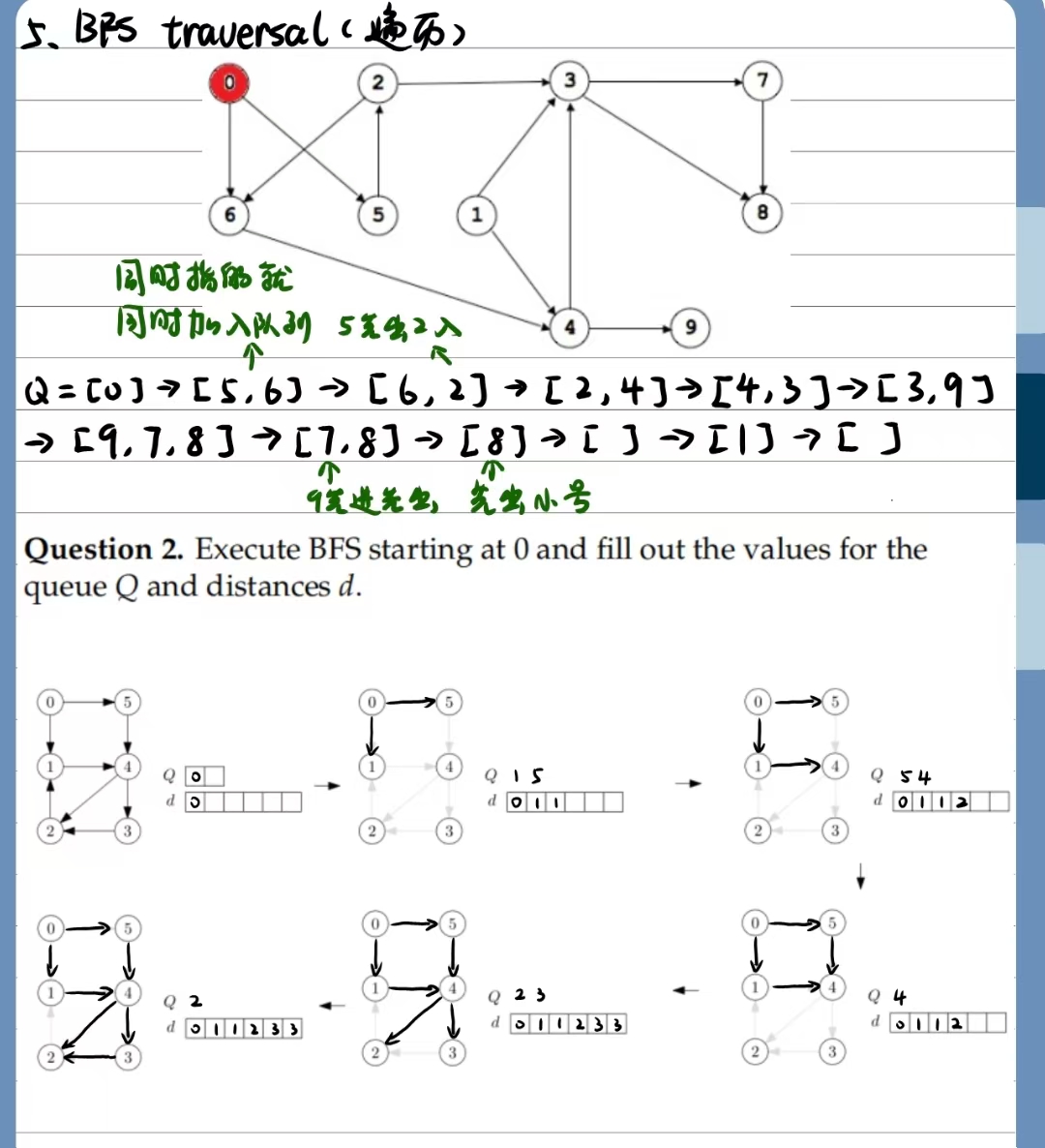
问题1:在下图中,从节点0开始分别运行深度优先搜索(DFS)和广度优先搜索(BFS)。绘制相应的搜索树。
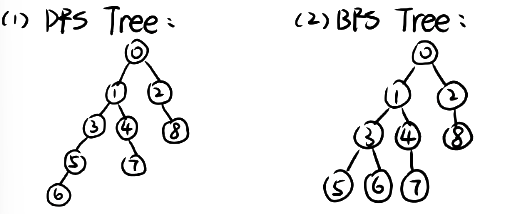
问题2. 从0开始执行广度优先搜索(BFS),并填写队列Q和距离d的值
图的应用
Lecture 16 Distances in Weighted Graphs 加权图中的距离
1.带权图的定义:在实际应用中,我们需要计算带权图中的距离,带权图是指边具有整数权重的图。
加权图(Weighted Graph)是
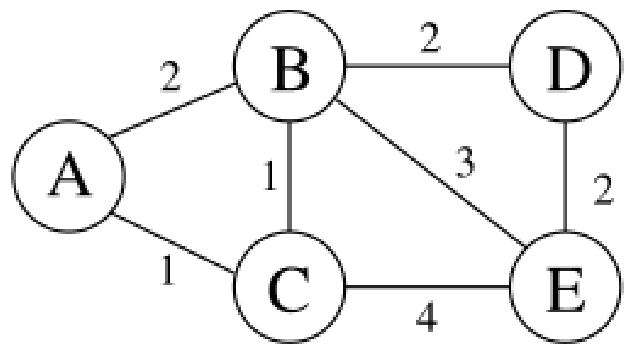
2.加权图表示
我们将邻接矩阵或邻接表表示法扩展到加权图。
adjacency matrix邻接矩阵:
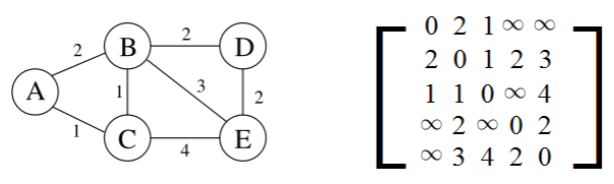
adjacency list邻接表:
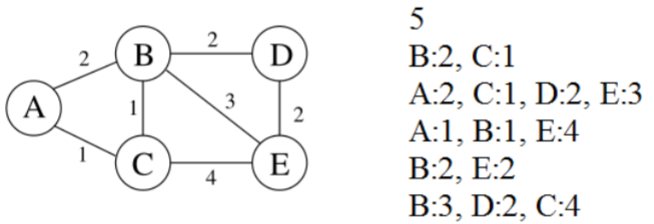
3.Shortest Path Problem (Single-Sourced)
输入:一个带权图G和一个源节点s INPUT: a weighted graph G and a source node s
输出:从s到所有其他节点的最短路径。OUTPUT: the shortest path from s to all other nodes.
4.Priority Queue优先队列
优先队列是一种数据结构,它存储一组(元素,键)对,其中元素的键是一个整数值,并且支持以下操作:
Insert (e, k) : Add a new element e with key k to the collection向集合中添加一个带有键k的新元素e
DeleteMin(): Return the element with the smallest key, and remove it from the collection返回具有最小键的元素,并将其从集合中移除
ResetKey(e, k) : Reset the key value of element e to a smaller value k将元素e的键值重置为更小的值k
5.迪杰斯特拉算法的伪代码
Algorithm Dijkstra(G,s)
1 | INPUT: A weighted graph G, and a node s |

6.Dijkstra时间复杂度
①Linked List链表:
在存在大量边的情况下更受青睐,即
②Binary Heap二叉堆:
Question 1. On the graph below, run Dijkstra’s algorithm starting from node 0. Draw the content of the priority queue at each step, and the shortest paths found from 0 to all nodes.
问题1:在下面的图中,从节点0开始运行迪杰斯特拉算法。在每一步都画出优先队列的内容,以及从0到所有节点的最短路径。
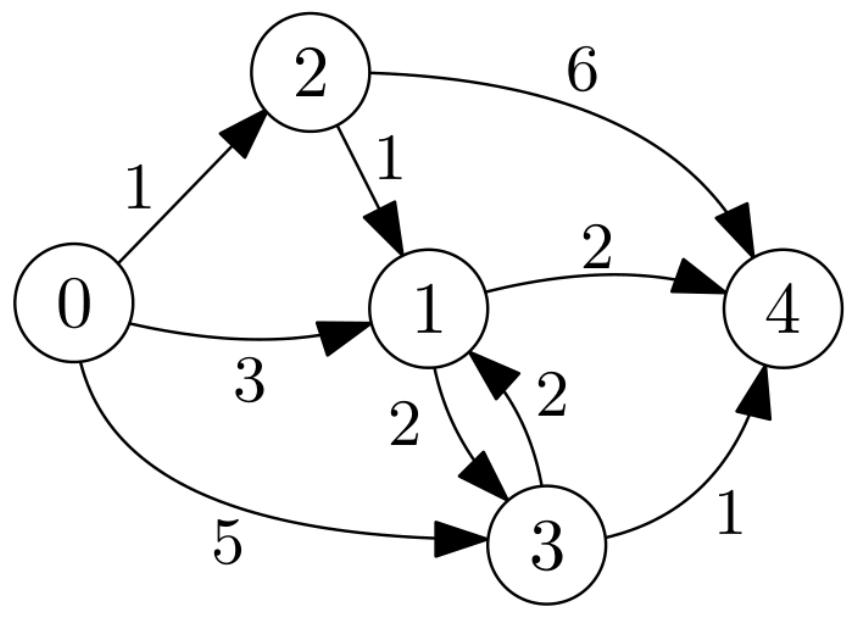

Question 2. Suppose you would like to find the longest path from a given node to other nodes in a weighted directed acyclic graph1. Someone suggests that maybe we can try modifying Dijkstra’s algorithm, so that instead of using a min-heap (as we do for dijkstra’s algorithm), we use a max-heap, i.e., a priority queue where we have DeleteMax operation that returns and removes the maximum element, and update the value
问题2. 假设你想在一个带权有向无环图中找到从给定节点到其他节点的最长路径。有人建议或许可以尝试修改迪杰斯特拉算法,不用最小堆(就像我们在迪杰斯特拉算法中所做的那样),而是用最大堆,即一种具有“删除最大值”操作(返回并移除最大元素)的优先队列,并且每当我们找到到节点v的更长路径时,就更新节点v的值
No. Dijkstra Algorithm is greedy: nodes are finalized immediately when popped. A Max-Heap prioritizes immediate long edges (e.g., direct path
Lecture 17 Minimal Spanning Trees最小生成树
1.生成树相关定义
①如果图G本身是一个连通分量,则图G是连通的。
②G的生成树是一个连通子图,它包含V中的所有节点且没有环。
③A minimal spanning tree of a weighted graph is a spanning tree whose total weight is minimal.加权图的最小生成树是总权重最小的生成树。
注意:最小生成树可能不是唯一的。
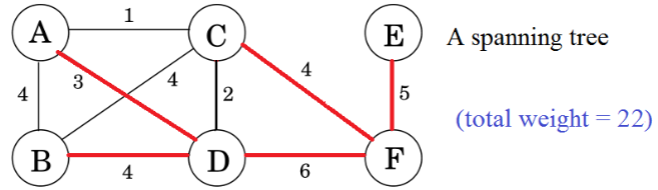
2.Minimal Spanning Tree (MST) Problem最小生成树(MST)问题
INPUT: A weighted connected (undirected) graph
OUTPUT: A MST of
注意:这又是一个树的构建问题,就像图的遍历和最短路径问题一样。
3.贪心算法引入
(1)Optimisation Problem最优化问题
一个优化问题包含一个解集,其中每个解都有一个值。该问题要求找到具有最大值/最小值的解(即最优解)。
(2)Optimised Tree Construction in Weighted Graphs带权图中的优化树构造
目标:在图中构建一棵作为最优解的树
最优子结构:如果S是一个最优解,那么S的任何子部分也是一个最优解。Optimal Substructure: If S is an optimal solution, then any subpart of S is also an optimal solution.
(3)最短路径问题
目标:在图中构建一棵树,使从s到其他节点的距离最小。
最优子结构:如果
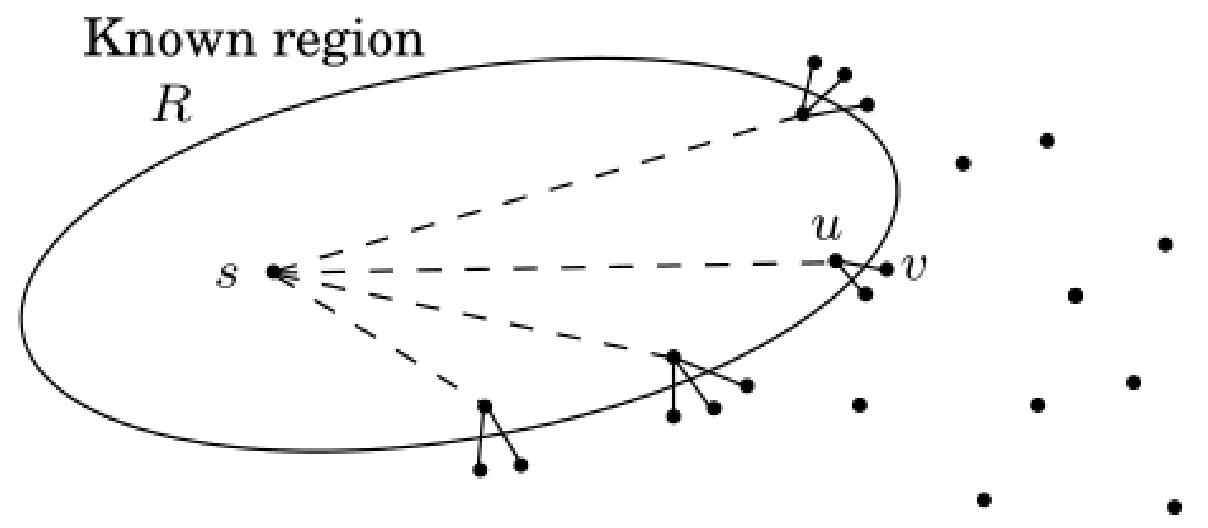
贪心选择:假设R是“已知区域”,v是R之外且能使当前距离最小的节点。那么,我们可以安全地在下一步将v加入R中。
(4)Minimal Spanning Tree Problem最小生成树问题
目标:在图中构建一棵树,使树的总权重最小。
最优子结构:如果T是图G的一棵最小生成树,且v是T中的一片叶子,那么从T中移除v后,我们会得到G中移除v后的子图的一棵最小生成树。
贪心选择Greedy Choice:我们能否获得与最短路径问题类似的性质?
4.Cut Property切割性质 (Version 1.0)
设
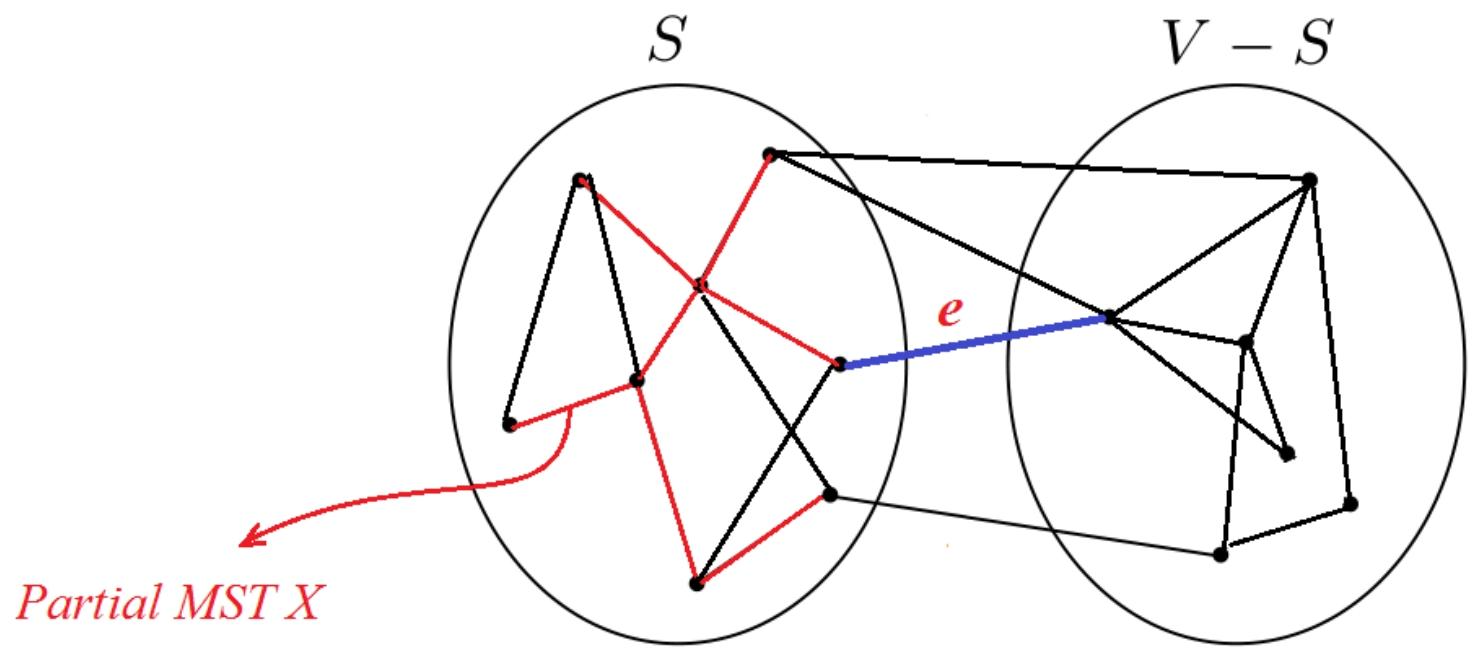
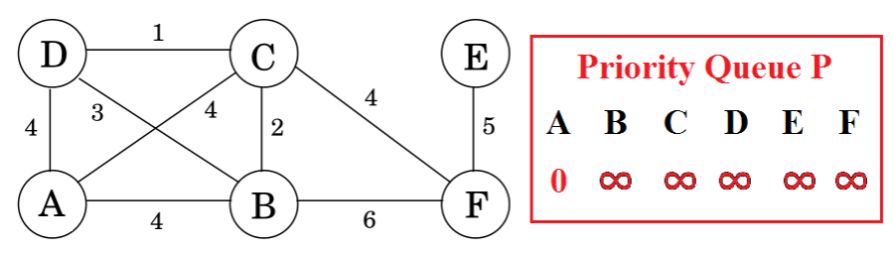
5.Prim’s Algorithm普里姆算法
以与迪杰斯特拉算法类似的方式找到最小生成树。维护一个已知区域的集合。为每个节点u维护
直观的说就是一个结点一个结点的遍历(A->B…->F)然后依次产生对应优先队列最后再合起来
6.Prim’s Algorithm普里姆算法伪代码
1 | Algorithm MST_Prim(V,E,w) |



Lecture 18 Kruskal’s Algorithm and Disjoint Sets 克鲁斯卡尔算法与不相交集合
1.Cut Property (Version 2.0)
①Version 1.0回顾:设
②我们称图G的一个部分最小生成森林partial Minimal Spanning Forest(MSF)是可能形成最小生成树(MST)的边的子集。假设我们已经构建了一个部分最小生成森林X。设e是该部分最小生成森林(MSF)中任意两棵树之间的最轻边。那么
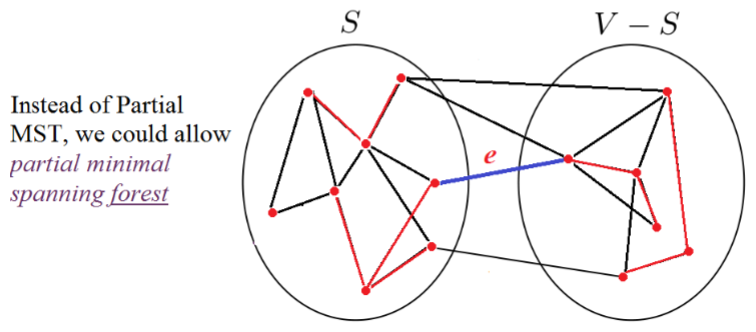
2.Kruskal’s Algorithm算法过程
简单来说就是由小到大依次选择权重最小的边(注意不能选择会导致成环的边哪怕它权重小)加入图上并更新不相交集合,把联通了的点放在一个圈圈里,直到所有点都被连接上。
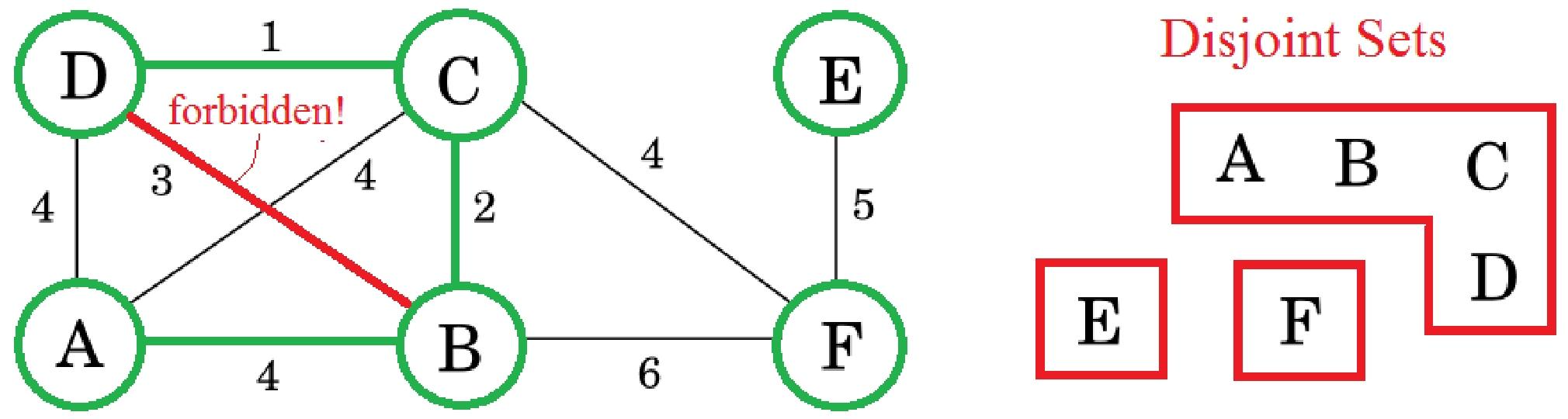 CD、BC、AB边那么不相交集合就要改成图上的样子,选边的时候不能产生环。
CD、BC、AB边那么不相交集合就要改成图上的样子,选边的时候不能产生环。
3.不相交集合与Kruskal’s Algorithm伪代码
(1)不相交集合(disjoint-sets data structure):不相交集合数据结构维护着一个不相交集合的集合(a collection of disjoint sets),其中每个集合都有一个唯一的代表元素,并支持以下操作:
①
②
③
1 | MST_Kruskal(V,E,w) |

4.Kruskal’s Algorithm: Complexity克鲁斯卡尔算法的时间复杂度
克鲁斯卡尔算法的运行时间取决于排序算法的复杂度和并查集操作的复杂度。
①
②
③
Running time for MST Kruskal:
具体来说,克鲁斯卡尔算法在不同的不相交集合实现中具有不同的运行时间:
①Arrays数组:
②Trees树:
③Trees with Path Compression带路径压缩的树:

贪心算法与图
Lecture 19 Greedy Algorithms 贪心算法
1.Dijkstra, Prim and Kruskal相似性
所有这些算法都可以被视为贪婪的怪物(greedy monsters):在每次迭代中,做出在当前情况下看起来最佳的决策。
①迪杰斯特拉算法(
②普里姆算法(
③克鲁斯卡尔算法(

2.贪心选择性质Greedy Choice Property
(1)Dijkstra, Prim and Kruskal三个例子的情况
①Dijkstra:如果从S到X中任何节点的距离都是最优的,那么子树X就是部分最短路径树。假设X是S上的一个部分最短路径树,且
A subtree X is a partial shortest path tree if the distance from S to any node in X is optimized. Suppose X is a partial shortest path tree on S and v \notin S is a current closest node via edge (u, v). Then X \cup{(u, v)} is also a partial shortest path tree.
通俗的讲就是已经有了一棵最短路径树了(子树),下一个添加的边如果是和这棵树距离最近的点连接起来的,那么这也是一棵部分最短路径树
②Prim’s:如果子树X可以扩展为一个最小生成树(MST),那么它是部分(partial)最小生成树(MST)。假设X是S上的一个部分最小生成树,而
A subtree X is a partial MST if it can be extended to an MST. Suppose X is a partial MST on S and
③Kruskal’s:如果子图X可以扩展为最小生成树(MST),那么它是部分最小生成森林(MSF)。假设X是一个部分最小生成森林(MSF),且
A subgraph X is a partial MSF if it can be extended to an MST. Suppose X is a partial MSF and
3.贪心算法的定义与内容
(1)定义:贪心算法通过在每次选择时做出局部最优选择来解决优化问题。A greedy algorithm solves an optimisation problem by making a locally optimal choice at each time.

(2)内容:
①全局优化值(Global optimisation value):这是一个用于评估解决方案的函数。Global optimisation value: This is a function used to evaluate a solution.
例如:Shortest Path: The distance最短路径:距离
MST: The sum of chosen edges最小生成树:所选边的总和
全局最优解(global optimum)是达到最理想的全局优化值的解。The global optimum is a solution that reaches the most desirable global optimisation value.
②局部优化值(Local optimisation value):这是一个用于评估单步可能移动的函数。
例如:Shortest Path: The estimated distances to a node so far最短路径:到目前为止到某个节点的估计距离
MST: The length of an edge MST:边的长度
警告:局部最优解不一定是全局最优解!Warning. A local optimum is not necessarily a global optimum!
E.g. Shortest path with negative weights.
(3)解题方法General Strategy
从一个空解开始,重复以下步骤:Starting with an empty solution, repeat the following steps:
①检查扩展当前解决方案的所有方法Examine all ways to expand the current solution
②选择能提供最佳局部优化值的方式Select the way that gives the best local optimisation value
当没有办法扩展解决方案时,该过程就会停止。The process stops when there is no way to expand the solution
4.示例1:部分背包问题Example 1: Fractional Knapsack Problem
A burglar enters a store and finds n items: the
Constraint: The thief’s knapsack can only carry
Goal: Maximize the total value of items in the knapsack.
一名窃贼进入一家商店,发现了n件物品:第
Knapsack Problem背包问题
INPUT: Values
OUTPUT: A selection of


(1)Local Optimisation Value:At each step, we optimise the
(2)Greedy Choice Property:
Suppose
We make another greedy choice:
①Take the remaining item with highest value/weight ratio, say
②Add
Then the resulting solution $S^{'} $is also a partial optimal solution.那么得到的解S'也是一个部分最优解。
代表第 个物品当前“剩余可用”的重量。
初始状态(Iteration 0):还没有拿走任何物品,所以
等于该物品的原始总重量 。 算法过程中:这是一个分数背包问题(Fractional Knapsack),意味着你可以拿走物品的一部分。虽然在这个贪心算法的逻辑里,除了最后一次装满背包的操作外,通常都是将物品“整个拿走”,但从数学定义的严谨性上,
追踪的是还没有被放进背包的那部分物品重量。
决定了你在这一步实际往背包里装入了多少重量的物品 。 这里有两个变量:
(W prime):背包当前剩余的容量(即还能装多少东西)。 (w_j prime):物品 剩余的重量(即货架上还剩多少)。 取
(最小值)是因为只有两种情况:
- 情况一:背包很大,装得下整个物品 (
)
- 我们选择
。意思是把这个物品全部拿走。 - 情况二:背包空间不够了,装不下整个物品 (
),通常对应最后一个装入的物品体积太大而背包体积剩余不足就只能装下部分,就会涉及到这个判断
- 我们选择
。意思是把背包填满,此时只能拿走物品 的一部分(分数部分)。 简单来说: 这行公式的意思就是“能拿多少拿多少,直到把物品拿光或者把背包装满为止” 。
Example
Example W = 100 , w = [20,25,50,40,30, 60] , v = [70,125,80, 80,120, 60] .

是一个优先级队列(Priority Queue)或者一个排序后的列表,里面的每一项是一个有序对 。
- 第一项 (Index): 代表物品的下标(第几个物品)。
- 第二项 (Ratio): 代表该物品的“价值密度”,即 $\frac{\text{价值 } } {\text{重量 } } $ (
)。贪心算法的核心就是优先拿“价值密度”最高的物品。 给定数据:
(重量) (价值) 计算每个物品的性价比 (Value / Weight):
- 物品 0:
- 物品 1:
- 物品 2:
- 物品 3:
- 物品 4:
- 物品 5:
生成的集合
: PPT里的
是按照这些计算结果组成的对子:
- 物品 1 性价比最高 (5),所以有
- 物品 4 性价比第二 (4),所以有
- 物品 0 性价比第三 (3.5),所以有
- 以此类推...
所以你在图片 Iteration 0 中看到的
: 正是按照性价比从高到低排列的物品顺序。算法会按照这个顺序依次尝试把物品装入背包。

其中
就是处理后的列表(存放的是index+重量而不是价值比); 就是更新后重量列表,那1放进去之后对应的它的重量就变为0; 就是剩余背包容量; 就是现有的价值数



Interation 4因为W’已经只剩25了,不足以把index=3地物品全塞进来,就只能塞部分,所以塞25/40=5/8,那么价值也是加
,然后更新W’=0
1 | Algorithm FracKnapsack(v[1 . . n] , w[1..n], W) |

5.示例2:活动选择问题Example 2: Activity Selection Problem
Scenario:
Select the activities so that we maximize the number of activities to attend, under the constraint that we do not attend two activities at the same time and we always attend an entire activity.
选择活动,以便我们能参加的活动数量最大化,在我们不能同时参加两项活动且必须全程参加一项活动的限制下。
Activity Selection Problem:

输入:由
输出:不重叠的活动集合
重叠的Overlapping
Local Optimal Value:
The finishing time of activities 活动的结束时间
At each step, we choose the activity that finishes the earliest 在每一步,我们选择最早结束的活动
Greedy Choice Property:
Suppose there is an optimal selection S that doesn’t consist of activity i. 假设存在一个不包含活动i的最优选择S。
Then replacing the activity that finishes first in S by i, we still have an optimal selection. 那么,用活动i替换S中最先结束的活动后,我们仍然得到一个最优选择。
1 | Algorithm ActivitySelect(begin[1..n], end[1..n]) |

Note: The greedy choice property ensures that global optimum = Local optimum.However, this property does not hold in general.(贪心这种求局部最优解代替全局最优解的思想并不是总是成立)
Lecture 20 Shortest Paths, Revisited 最短路径(再探)
1.Recap: Being Greedy is Risky. Dijkstra’s algorithm does not work for weighted graph where the weights could be negative. Greedy choice does not work here.回顾:贪心是有风险的,迪杰斯特拉算法不适用于权重可能为负数的加权图。
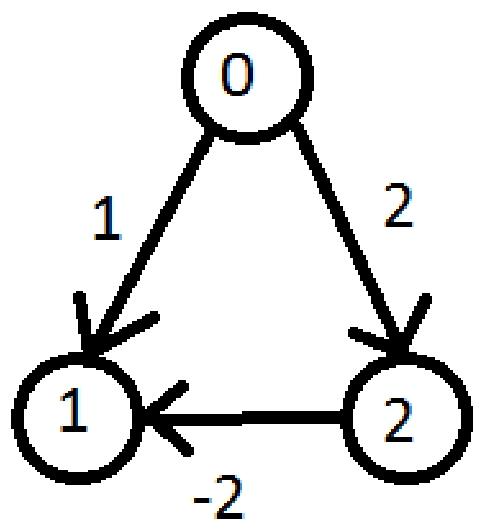
2.Paths with Bounded Length有界长度路径:Let
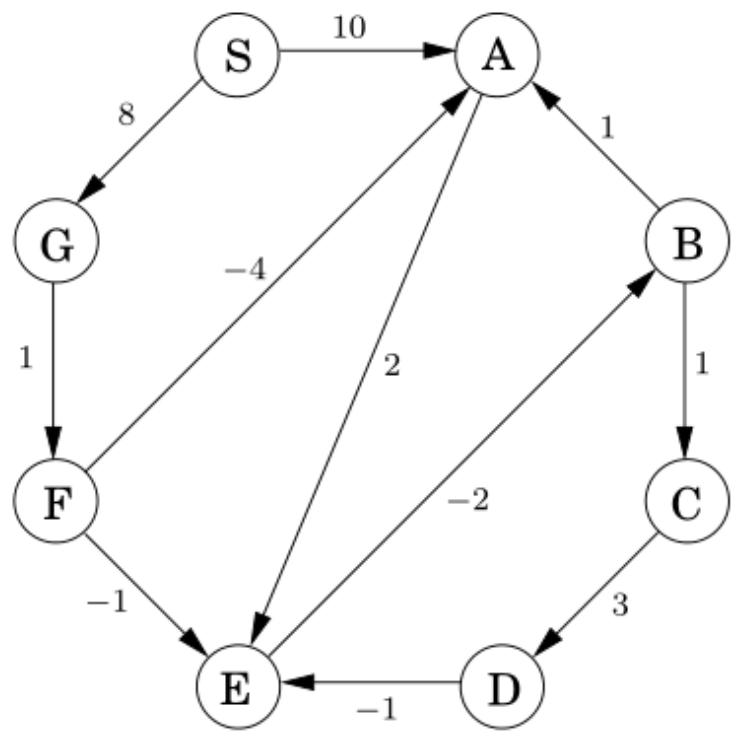
下面的值就代表了S到某个节点在经过不同边数量的条件下路径长度的情况:
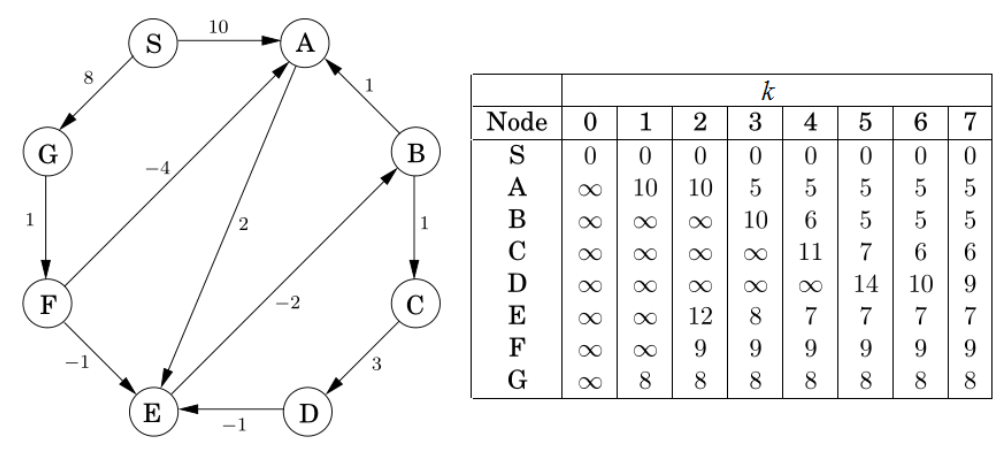
- Computing
for every
- Computing
for every out-neighbour of
- Computing
How can we tell that
and So 以此类推
所以引入Bellman-Ford Algorithm:对于任意
1 | Algorithm Bellman-Ford(G,s) |

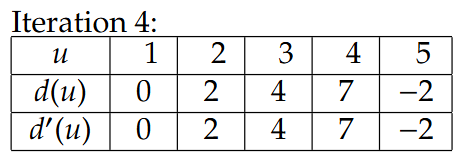
Example
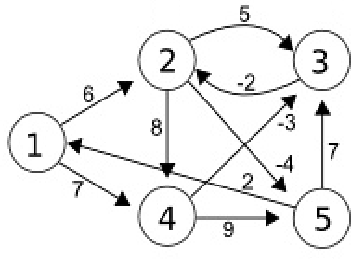
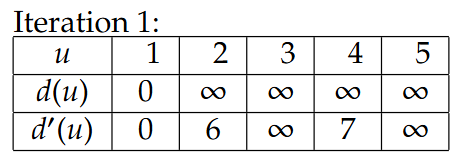
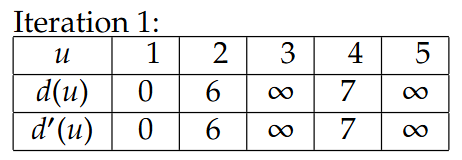
相当于第二排的d’(u)先给出更新后数值,然后再更新到d(u)里,后面的Iteration也是一样的
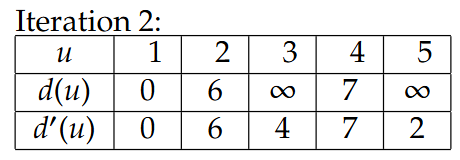
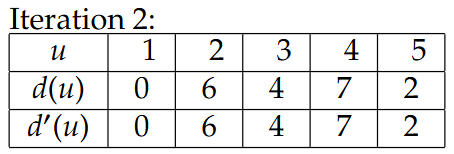
这里的-2是指1->5成环了,那么5->1是2,反过来1->5就是-2
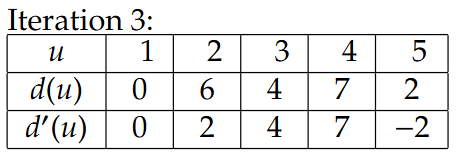
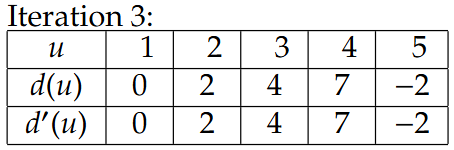
3.All-Pair Shortest Path所有节点对的最短路径(即Bellman-Ford时间复杂度分析)
- Compute the shortest distance between any pair of nodes in G
Dijkstra’s and Bell-Ford algorithm both solves Single-Source Shortest Path Problem.迪杰斯特拉算法和贝尔-福特算法都能解决单源最短路径问题。
Solution: Run the single-source algorithm n times, each time from a different node! 解决方案:运行n次单源算法,每次从不同的节点开始!
Note:
①m could be as large as
We would like a faster algorithm for this problem.(即Floyd-Warshall Algorithm)
4.Floyd-Warshall Algorithm弗洛伊德算法(动态规划引入)
Label all nodes using
Define
Fact:
那么
的 指的是能经过的节点范围,比如说k=2即 那么能经过的结点就是 ;k=3即 就是
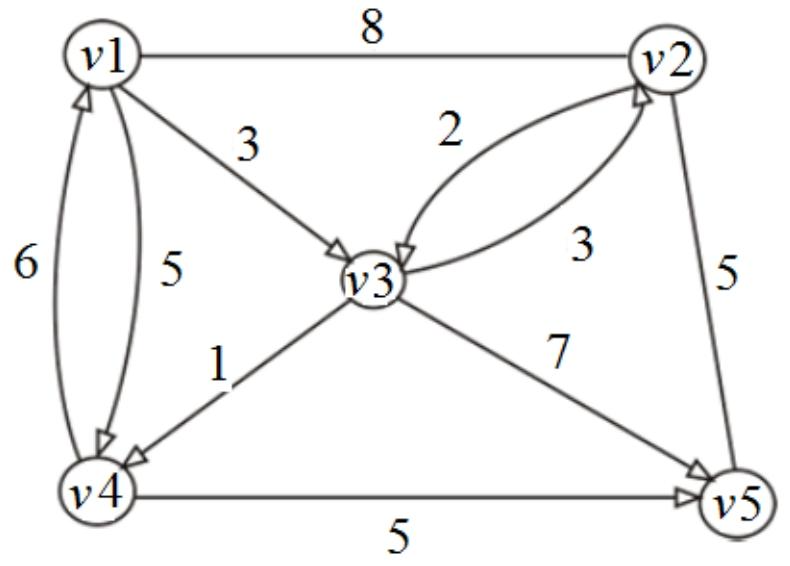
Example: Going from 1 to 5:
Able to pass through
Able to pass through
Able to pass through
解题过程:
Suppose G does not contain a negative cycle.假设G不包含负环。
①Computing
②Computing
Optimal Substructure: Suppose
Therefore we have:
5.Floyd-Warshall Algorithm伪代码
1 | Floyd-Warshall(G) |
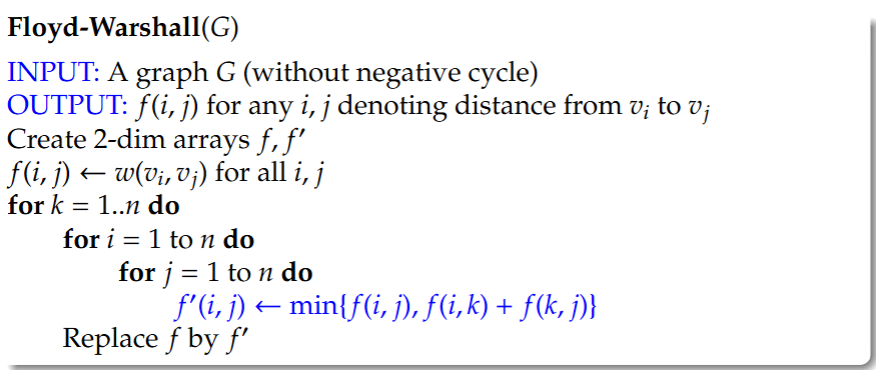
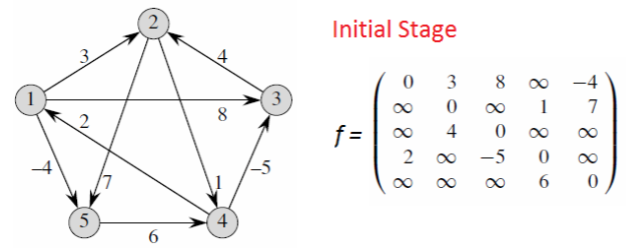
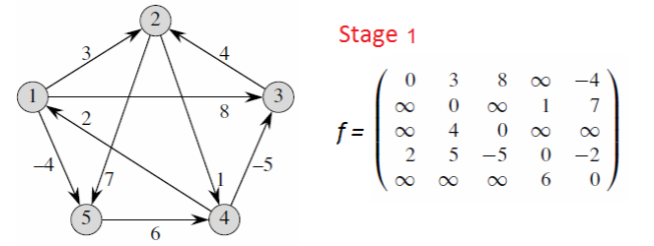
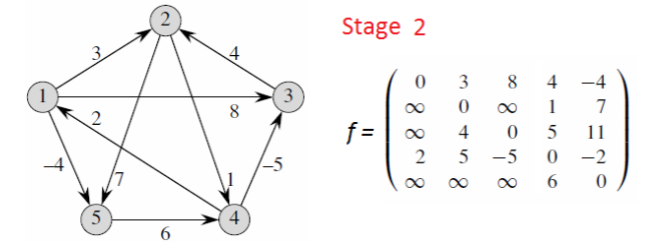
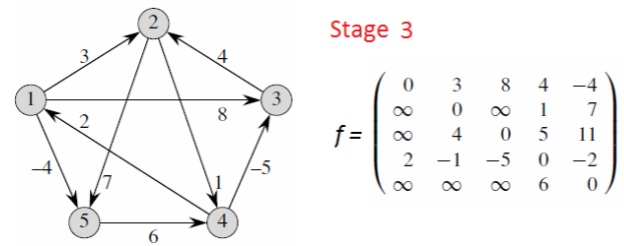
逻辑就是一开始只能获取相邻节点的边的数值,随着轮次扩大慢慢更新为相邻节点的相邻节点的遍历
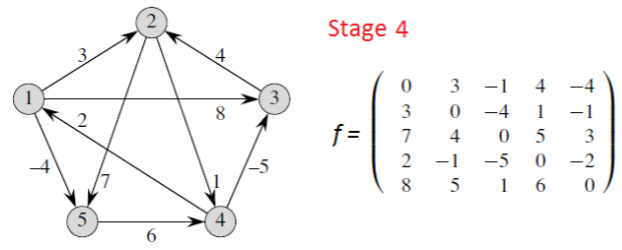
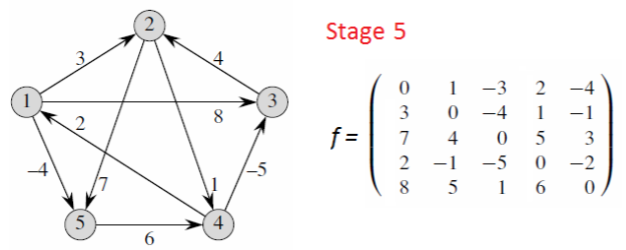
时间复杂度:
6.Shortest Paths, A Summary(可能出简答题)
(1)Single-Source Positive Weights: Dijkstra’s algorithm单源正权值:迪杰斯特拉算法
Complexity: Depends on the priority queue implementation复杂度:取决于优先队列的实现
①List
②Binary Heap
③Fibonacci Heap
(2)Single-Source Positive/Negative Weights: Bellman-Ford algorithm 单源正负权重:贝尔曼-福特算法
Complexity:
(3)All-Pair: Floyd-Warshall algorithm 全对:弗洛伊德-沃肖尔算法
Complexity:
All-Pair Shortest Path (全顶点对最短路径) 问题解决的是:“图中任意两个点之间的最短距离是多少?”
1.核心区别:从“一对多”到“多对多”
- Single-Source (单源最短路径):
- 代表算法: Dijkstra, Bellman-Ford。
- 场景: 你只关心从某一个特定的起点(比如
)出发,到图中所有其他点( )的最短距离。 - 结果: 通常得到一个列表或数组,表示
到各点的距离。 - All-Pairs (全顶点对最短路径):
- 代表算法: Floyd-Warshall。
- 场景: 你想知道图中任意起点到任意终点的最短距离。比如
到 , 到 , 到 等等所有组合。 - 结果: 通常得到一个 二维矩阵 (Matrix)。课件第 38-43 页展示的那个
的表格 就是典型的 All-Pairs 的结果 3333。矩阵中第 行第 列的值,就代表从节点 到节点 的最短距离。 2.为什么要把它单独列出来?“我把 Dijkstra 或者 Bellman-Ford 算法对图中的每一个点都运行一遍,不就是 All-Pairs 了吗?”
笨办法: 是的,你可以对
个点分别运行 次单源算法。 代价太高: 如果图很稠密(边很多),运行
次 Bellman-Ford 的时间复杂度会达到 ,这太慢了。 更好的办法: 专门解决 All-Pairs 问题的 Floyd-Warshall 算法利用了动态规划的思想,可以在
的时间内一次性算出所有点对的距离。
Question: Compare Dijkstra, Bellman-Ford, and Floyd-Warshall algorithms regarding their problem scope, edge weight constraints, and time complexity.
(1)Dijkstra's Algorithm:
①Scope: Single-Source Shortest Path.
②Weights: Positive weights only.
③Complexity: Depends on implementation, e.g.,
with a Binary Heap. (2)Bellman-Ford Algorithm:
①Scope: Single-Source Shortest Path.
②Weights: Supports Positive and Negative weights.
③Complexity:
. (3)Floyd-Warshall Algorithm:
①Scope: All-Pair Shortest Path.
②Weights: General weights (no negative cycles).
③Complexity:
.
动态规划与图
Lecture 21 Dynamic Programming 动态规划
1.Optimisation优化
(1)一个优化问题包含一个解集,其中每个解都有一个值。该问题要求找到具有最大值/最小值的解(最优解)。
(2)优化问题示例:最短路径、最小生成树、背包问题、排序
- 排序(重新表述):将一组数字排列成一个序列
2.Sorting VS Shortest Path排序与最短路径( 可能出简答 )
(1)Similarity: [Optimal Substructure] 相似度:[最优子结构]
①Sorting: In a sorted array, any subarray is also sorted. 排序:在一个排序数组中,任何子数组也是排序好的
②SP(Shortest Path): In a shortest path, any segment is also a shortest path. 最短路径(SP):在最短路径中,任何一段也都是最短路径
⇒ both problems can be solved by “division”. 这两个问题都可以通过“分割”来解决。
(2)Difference: Suppose we divide the problem into subproblems 不同点:假设我们将问题分解为子问题
①Sorting: The subproblems are completely independent. Hence a top-down algorithm is suitable。排序:子问题是完全独立的。因此自上而下的算法是合适的
⇒ Divide and Conquer 分治法
②SP: The subproblems overlap. Hence a bottom-up algorithm is suitable. 最短路径(SP):子问题相互重叠。因此自底向上的算法是合适的。
⇒ Dynamic Programming 动态规划
3.Dynamic Programming
(1)Dynamic programming is a method for solving complex optimisation problems by breaking them down into simpler subproblems. 动态规划是一种通过将复杂的优化问题分解为更简单的子问题来解决这些问题的方法。
(2)It is applicable to problems exhibiting the properties of overlapping subproblems and optimal substructure. 它适用于具有重叠子问题和最优子结构性质的问题。
(3)Dynamic programming solves the subproblems from small to large to avoid duplication. 动态规划从小到大解决子问题,以避免重复计算。
3.Example: Single-Source Shortest Path示例:单源最短路径
1’ Bellman-Ford algorithm is an example of a dynamic program.
Four Steps of Dynamic Programming 动态规划的四个步骤
(1)Parametrize the problem: Divide the problem into subproblems indexed by a parameter:将问题参数化:将问题分解为按参数索引的子问题:
To compute distance, we compute
Parameter: Number of edges used in the shortest path. 参数:最短路径中使用的边数。
(2)Handle the base case
(3)Write a recurrence for larger subproblems
(4)Fill the table of partial solutions in a bottom-up way
Start from
2’ Floyd-Warshall algorithm is an example of a dynamic program.
(1)Parametrize the problem: Divide the problem into subproblems indexed by a parameter:
To compute distance, we compute
Parameter: Indices of nodes used as intermediate nodes. 参数:最短路径中使用的边数。
(2)Handle the base case
(3)Write a recurrence for larger subproblems
(4)Fill the table of partial solutions in a bottom-up way
Start from
3’ Floyd-Warshall algorithm is an example of a dynamic program.
(1)Parametrize the problem: Divide the problem into subproblems indexed by a parameter:
To compute distance, we compute
Parameter: Indices of nodes used as intermediate nodes. 参数:用作中间节点的节点索引。
(2)Handle the base case
(3)Write a recurrence for larger subproblems
(4)Fill the table of partial solutions in a bottom-up way
Start from $f_{1} $, then compute
4’ Example: Longest Increasing Subsequence
(1)问题背景
设
递增子序列是一个子序列
example: A sequence 5 2 8 6 3 6 9 7




(2)问题:Given a sequence
①Reformulate as a Graph Question重构为图问题
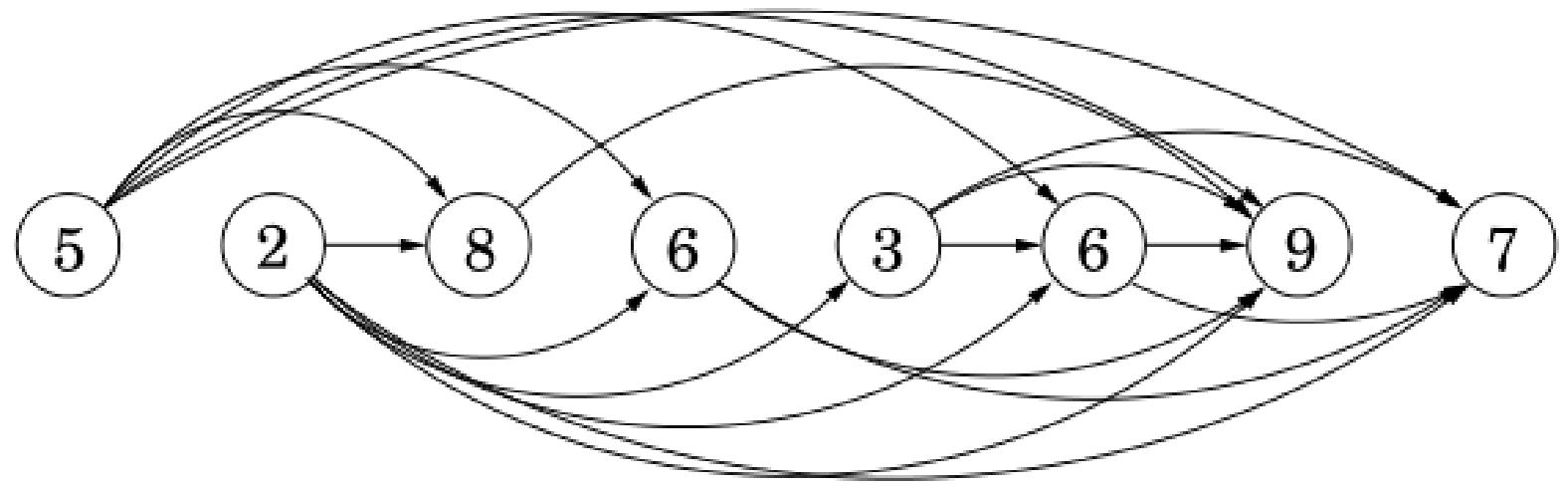
Create an edge
②Divide into Subproblems分解为子问题
Let
那么最长递增子序列的长度是:
③Base Case: The Smallest Subproblem
④Recurrence for Larger Subproblems
目标
:我们要计算以第 个数字结尾的最长递增子序列长度。 候选者
:我们需要回头看在 之前出现的所有数字(索引为 )。 条件
:这是最关键的过滤条件。根据图的定义,这意味着 。也就是说,只有当前面的数字比当前的数字小时,我们才能把当前数字接在它后面 。
:在所有满足条件(比当前数字小)的前面数字中,我们要找一个“最强”的队友——即那个已经拥有最长链条的数字 。
:一旦找到了最长的那个前驱 ,我们把当前的 接在它后面,所以总长度加 1。 通俗的大白话解释:我想知道以我(
)结尾能排出的最长队伍有多长。 我回头看了看排在我前面的所有人( )。 只有那些个子比我矮的人( ),我才能排在他们后面。 在这些个子比我矮的人里面,我挑了一个目前带着最长队伍的人,直接站到了他的身后。 所以,我的队伍长度 = 他的队伍长度 + 1(我自己)。
⑤Filling the Table
相当于一个节点一个节点遍历看看前面有没有节点指向自己,有则L+1并填入表中;比如L(8)这个就是2->3->6->7
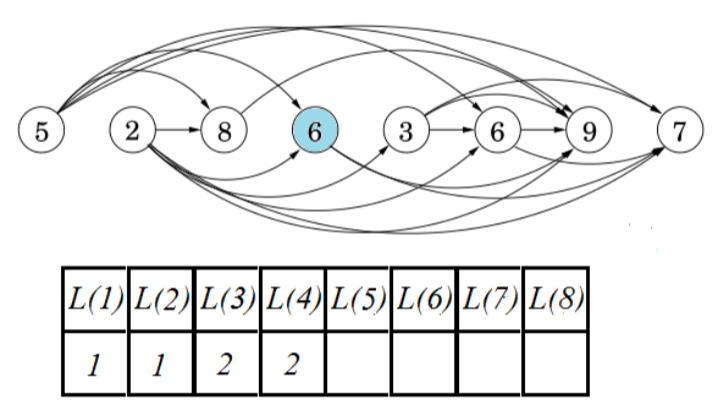
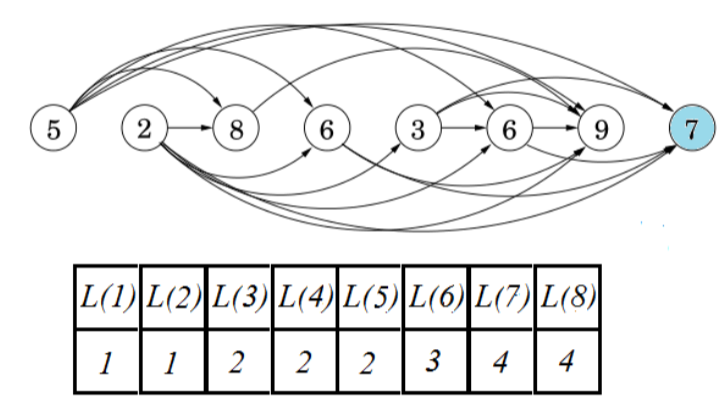
- Longest Increasing Subsequence伪代码
1 | LIS(a[1...n]) |

(3)形式化表达
①Parametrize the problem: Divide the problem into subproblems indexed by a parameter:
We compute
Parameter: The last node in the increasing subsequence参数:递增子序列中的最后一个节点
②Handle the base case
③Write a recurrence for larger subproblems
④Fill the table of partial solutions in a bottom-up way
Start from
5’ Edit Distance
(1)问题背景
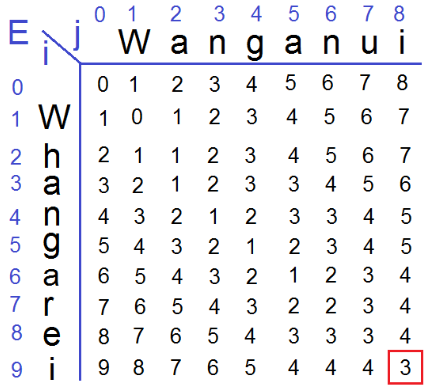
有些单词看起来相似,而有些单词看起来不同:Whangarei、Wanganui、Auckland
我们能否将这种相似性和差异性的概念形式化?我们能定义单词的距离度量吗?
Edit Distance:两个单词的编辑距离是将一个单词转换为另一个单词所需的最小编辑次数,这里的编辑包括字母的插入、删除和替换。

(2)问题:Given two words
Different ways of aligning the words result in different number of edits.单词的不同对齐方式会导致不同的编辑次数。
The edit distance problem asks for the best way to align the words.编辑距离问题寻求的是对齐单词的最佳方式。

情况1:x的最后一个字母与一个空格对齐。
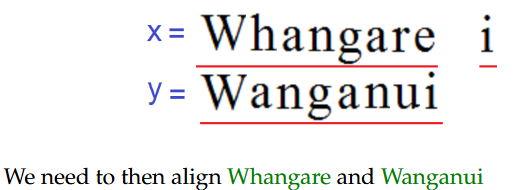
情况2:x的最后一个字母与y的最后一个字母对齐
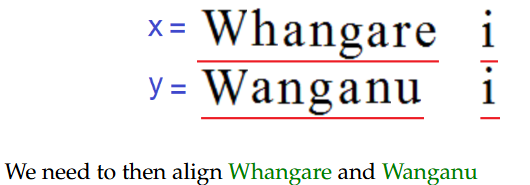
案例3:y的最后一个字母与一个空格对齐。
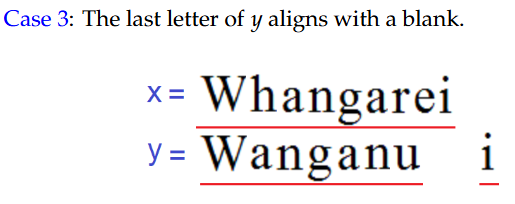
①Divide into Subproblems
Suppose we want to compute the edit distance of two words
Let
We would like to find
②Base Case: The Smallest Subproblem

③Recurrence for Larger Subproblem(目标就是求最右下角的那个数字)
$ E(i+1,j+1)=\operatorname* {min}{ E(i,j+1)+1,E[i+1,j]+1,E[i,j]+k}$
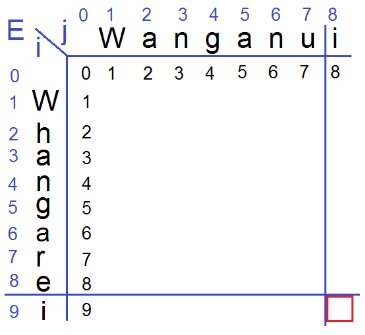
这个题意思就是把第i行的子单词(即单词的一部分)转变为第j行的字单词需要几步,直观的来说i-1相当于第i行的子单词删除了一个字母,比如Wha->Wh,i-1同时字母也少了一个;j+1就是插入一个字母,比如Wa->Wan就是插入了一个n;走斜对角线即i+1,j+1就是替换一个字母,比如Wh->Wa;填这个表就是先把行列数字写出来,然后按行为单位挨个填入数字。通常这个填入移动一个都是±1(+1对应下移i+1,右移j+1,斜下移(i+1,j+1),-1就是相反)。一般都会有一个特殊规则,比如这个匹配他就是如果下移字符等于右移字符那斜下移只需+0即可,对应实际情况就是W->W就是同一个字母替换那就是没替换,+0(这个过程比较复杂一定要自己结合ai去理解不太好解释)
- Edit Distance伪代码
1 | EditDistance(a[1..m],b[1..n]) |

(3)问题形式化
①Parametrize the problem: Divide the problem into subproblems indexed by a parameter:
We compute
②Handle the base case
③Write a recurrence for larger subproblems
④Fill the table of partial solutions in a bottom-up way
Start from $E(0, j) $, then compute
Lecture 22 Flow Network 流网络
1.Part I: Flow Network – Basic Terminology
(1)A Shipping Problem:一位农场主计划租用卡车将他的水果运往奥克兰。由于道路和交通状况,卡车在每对城镇u和v之间每天最多能运输c(u, v)箱水果。他每天最多能运输多少水果?
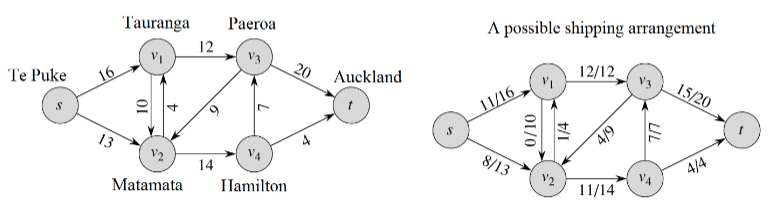
(2)Definition [Flow Network]
①A source node in a directed graph is a node with no incoming edges.有向图中的源节点是指没有入边的节点。
②A sink node in a directed graph is a node with no outgoing edges.有向图中的汇点是指没有出边的节点。
③A flow network is a directed graph (V, E, c, s, t) where (V, E, c) forms a weighted graph with positive edge weights,
流网络是一个有向图(V, E, c, s, t),其中(V, E, c)构成具有正边权重的加权图,
这个所谓的汇点就是理解为终点就好(相当于没有别的路可以出去了)
(3)Definition [Flow]
A flow in a flow network (
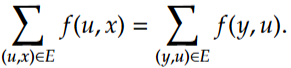
流网络中的流(V, E, c, s, t)是一个函数f: E \to \mathbb{N},使得对于每个(u, v) \in E,f(u, v) ≤c(u, v)都成立;同时对于任何既不是s也不是t的节点u,我们有上述公式成立
Intuitively, a flow defines a way to send oil from S to t without exceeding the pipeline capacity, and without any leak on the way.直观地说,流定义了一种从S向t输送石油的方式,这种方式不会超过管道容量,且途中不会有任何泄漏。
(4)Definition [Size of a Flow]
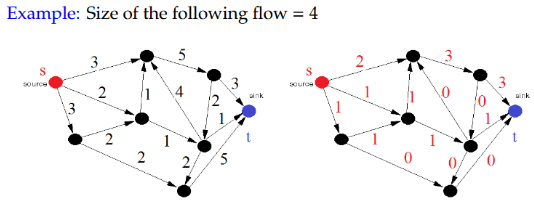
The size of a flow f in a flow network is
流网络中流f的大小是
在流网络算法(如Ford-Fulkerson算法)中,"Size of flow"是可以有多个值的,比如下面这个流绕的乱七八糟的就能弄出来是4,但是这也意味着是存在最大流的(也就是所有流里面的最大值)
(5)Definition [Maximal Flow]
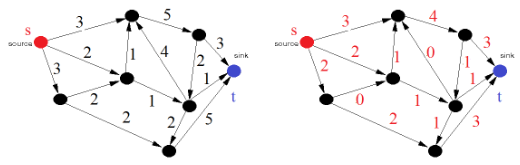
A flow in a flow network is maximal if it has maximal size.在流网络中,如果一个流的规模最大,那么它就是最大流。
(6)Definition [Cut]
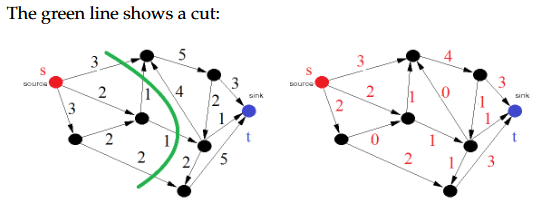
A cut in a graph is a set C of edges such that removing them would disconnect the graph into left(C)(nodes reachable from s) and the right part right(C) (nodes that may reach t ).图中的割是边的集合C,移除这些边会将图断开为left(C)(从s可达的节点)和右部分right(C)(可能到达t的节点)。
大白话就是随便从中间切一刀把节点划分为靠近s的和靠近t的集合,这一刀划掉的边就是割,那么割的容量就是这些边的权重之和
(7)Definition [Capacity of a Cut]
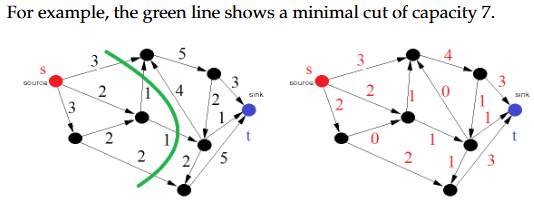
The capacity of a cut C in a flow network is the sum of the capacity of edges that goes from left to right: 流网络中割集C的容量是从左到右的边的容量之和(割一刀割到的边的权重之和)
A minimal cut is a cut with minimal capacity.最小割是具有最小容量的割。
(8)Cuts in a Flow
Let C be a cut in a network G and f be a flow. The net flow of f over C 设C是网络G中的一个割,f是一个流。f在C上的净流量为:
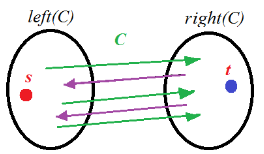
(9)Flow and Cut流和割
①Fact 1:For any cut C and flow f,
②Fact 2:For any flow network G,
(10)Two Problems:Max-Flow Problem & Min-Cut Problem
①Max-Flow Problem最大流问题
Given a flow network, find a maximal flow in the network? In other words, what is the maximal quantity we can send from s to t?给定一个流网络,如何找到该网络中的最大流?换句话说,我们能从s发送到t的最大量是多少?
②Min-Cut Problem
Given a flow network, find a minimal cut in the network? In other words, what is the bottleneck across the entire network?给定一个流网络,如何找到该网络中的最小割?换句话说,整个网络的瓶颈是什么?
稍后我们将证明这两个问题是同一个问题。
2.Part II: Max-Flow Min-Cut
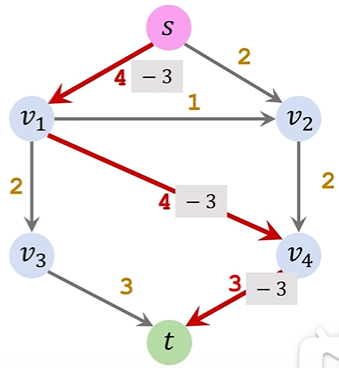
(1)A Network Example
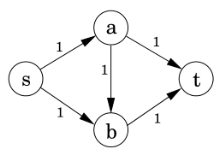
①Start with zero flow从零流开始
②Repeat: Choose a path from s to t and maximize flow along this path.重复:选择一条从s到t的路径,并使沿该路径的流量最大化。
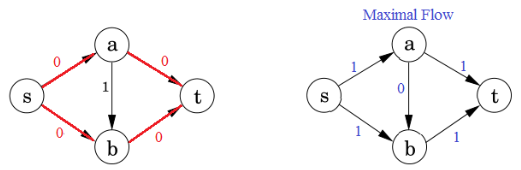
那么这样也会有一个问题:要是选错路了不能反悔就会导致这个流是一个阻塞流(blocking flow)不允许更多流到达汇点。
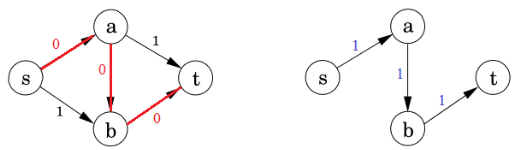
残差网络residual network:管道的空闲量。(红色数字对应的图)
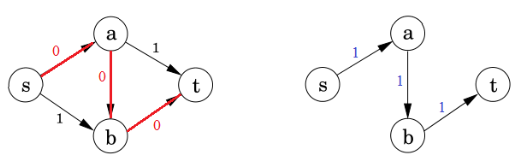
3.Solving Max-Flow Problem:Ford-Fulkerson Algorithm
1 | Ford-Fulkerson Algorithm |

ppt讲的有点不清楚,可以看下面的具体步骤执行:
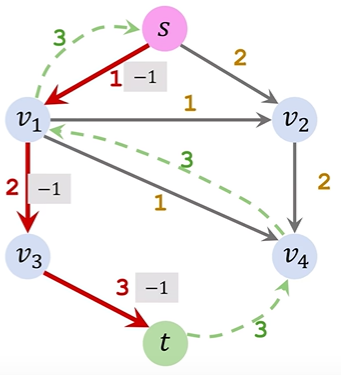
①Initialization&Update residuals&Remove saturated edges:正常选一条路,把residual graph(初始值是满的)相应的边数值去掉,数值去掉后为0的就把这条边直接去掉,还有剩余值的就更新
②Add a backward path:把扣了数值的边对应画一个反向边指回去,表示该路径可回溯
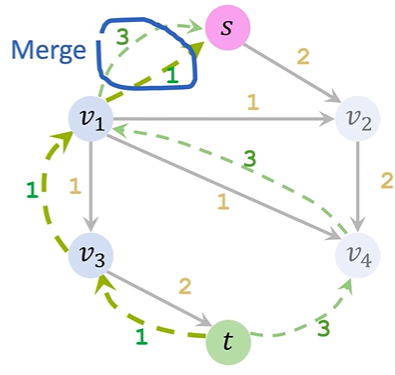
③Find an augmenting path&Merge:寻找一条新路径重复上述操作,对于两个节点间出现了两条同向反向路径,就给他合并为一条(哪怕是实线和虚线只要同向也合并)
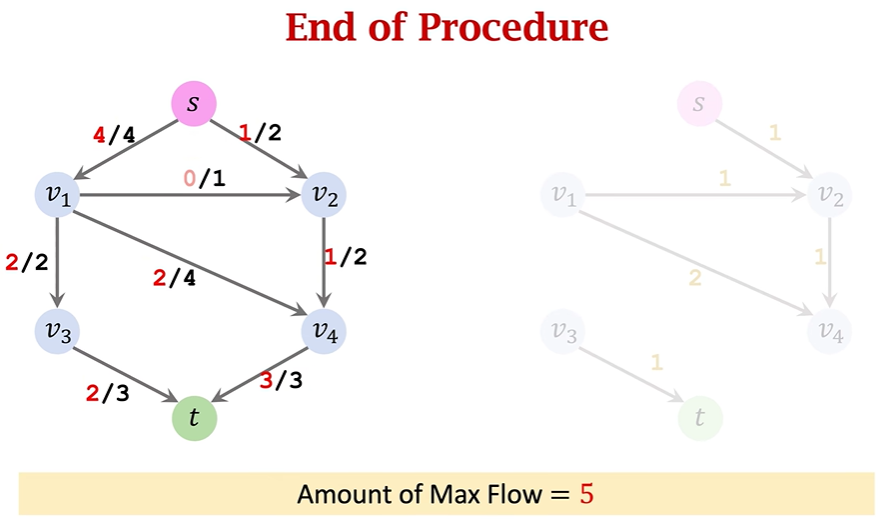
④算法结束后把所有反向路径去掉,留下的就是residual network,flow=capacity-residual也就是容量减去残差;总流量(也就是最大流大小)就看起点s出去了多少或者终点t流入了多少(x/y的x是流出的流量数值,y是通道的容量)
4.Max-Flow Min-Cut Theorem:In any flow network, the size of the maximal flow equals the capacity of the minimal cut.最大流最小割定理:在任何流网络中,最大流的规模等于最小割的容量。
Ford-Fulkerson algorithm finds a maximal flow, as well as a minimal cut in a network.福特-福克森算法可找出网络中的最大流以及最小割。
5.Flow Network/Ford-Fulkerson Algorithm的2 applications
(1)Application 1: Community Detection
扎卡里的空手道俱乐部 1 韦恩·W·扎卡里对一个空手道俱乐部的社交网络进行了研究,该俱乐部有34名成员,成员之间在俱乐部外有78个互动联系。在研究期间,管理员“约翰·A”和教练“嗨先生”之间发生了冲突,这导致俱乐部分裂成两个。一半的成员围绕嗨先生成立了一个新俱乐部,另一部分成员则找到了新教练或放弃了空手道。基于收集到的数据,扎卡里将俱乐部中除一人外的所有成员都正确分配到了他们在分裂后实际加入的群体中。
Question: How did Zachary come up with the partition?
Community Detection Problem
Partition a given network into subgraphs that capture “realistic communities” in real-life networks:(四个可能场景)
①Circles of friends
②Political bloggers with similar opinions
③Consumers with similar purchasing behaviours
④Functional groups of proteins (in protein-protein network)
(2)Application 2: Bipartite Matching二分匹配
一个在线交友网站上有m名男性用户和n名女性用户。通过分析他们的个人资料,我们将可能的匹配表示为一个 bipartite 图。现在需要找到一种将男性与女性匹配的方式,以使尽可能多的用户能够匹配成功。
Bipartite Matching
Let
A node
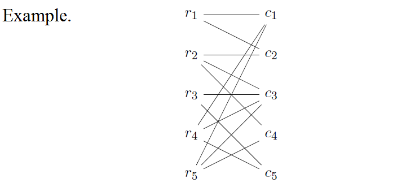
-
A matching M of G is maximal if it is not a proper subset of another matching of G如果图G的一个匹配M不是图G中另一个匹配的真子集,则M是极大匹配。
-
A matching of G is perfect if every node in G is matched.如果图G中的每个节点都被匹配,则G的匹配是完美匹配。
Maximal Bipartite Matching Problem: Given a bipartite graph, compute a maximal matching最大二分匹配问题:给定一个二分图,计算最大匹配
We can reduce the bipartite matching problem to maximal flow problem: Given a bipartite graph
①Add a source node s and a sink node t添加一个源节点s和一个汇节点t
②Add edges between s and all nodes in X 在s和X中的所有节点之间添加边
③Add edges between t and all nodes in Y 在t和Y中的所有节点之间添加边
④Set capacity of each edge to 1 将每条边的容量设为1
Then a maximal flow in the resulting network corresponds to a maximal matching.那么,所得网络中的最大流对应着最大匹配。
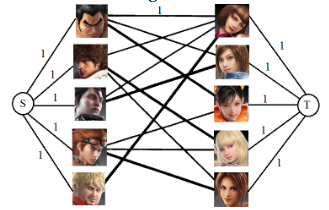

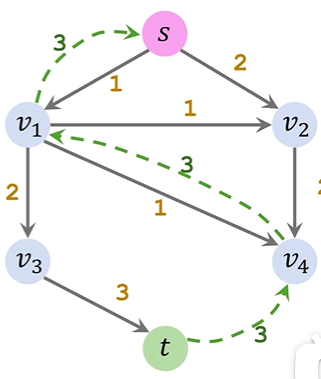
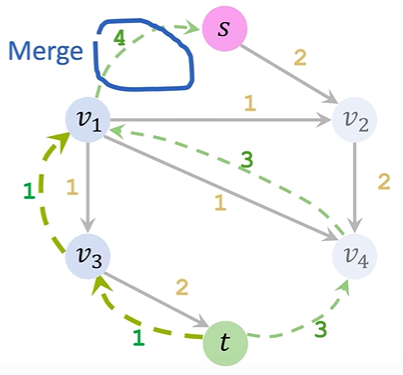
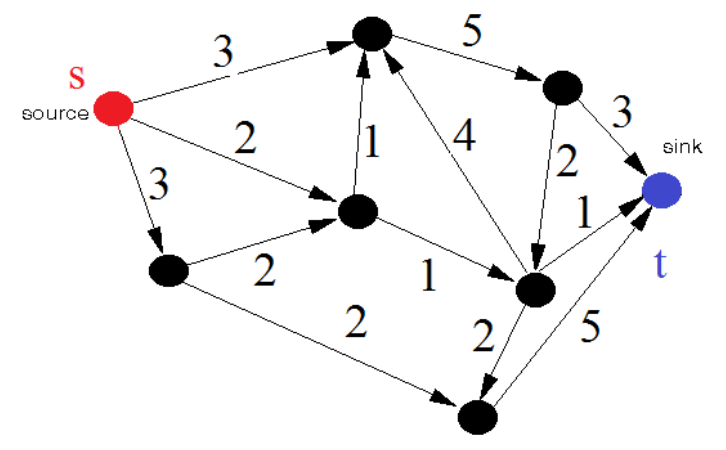
Question 1. Consider the following flow in the flow network. Write down its residual network.
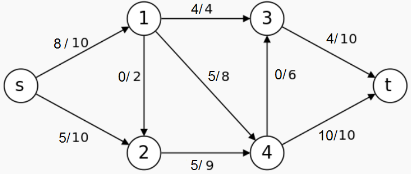
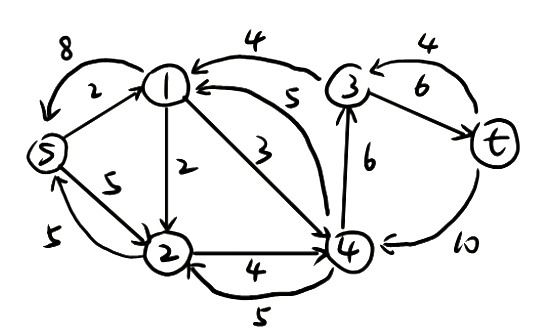
Question 2. Identify a path flow in the residual network you found for the question above, and co mbine it with the flow given.
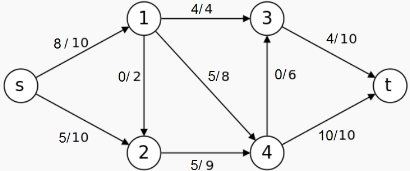
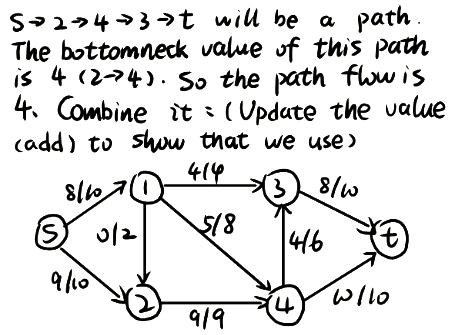
Question 3. Consider the flow network below. Apply Ford-Fulkerson’s algorithm to find a maximal flow and also identify a minimal cut in the network.
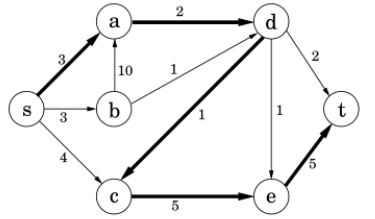

综合设计题专项突破
递归分治算法题模板
1 | function(n){ |
比如说MergeSort的模板对应为:
1 | function MergeSort(list input[0..n-1]) |
比如说QuickSort的模板对应为:
1 | function QuickSort(list a[0..n-1],integer i,integer j) |
作业题
代码题:分治可能考作业一第二题,贪心可能考作业二第三四题,动态规划是作业二第五题
1.分治:作业一第二题
English Question
Given two sorted arrays of length n, find the median of their union in
中文问题
给定两个长度为 n 的已排序数组,请在
English Answer
Solution: We will use a modified binary search algorithm to find the k-th smallest element in the union of two sorted arrays. 3The key idea is to eliminate parts of the arrays that cannot contain the k-th smallest element at each step, thus reducing the problem size logarithmically. 4
Define function find_kth_smallest(A, B, k) where A and B are the input arrays and k is the position of the desired smallest element. 5
Step 1. Base Cases:
- If one array is empty: Return the k-th element from the other array.
- If
Step 2. Recursive Step:
- Let
- Let
- If
- The first i elements of A cannot be the k-th smallest.
- Recursively call
find_kth_smallest(A[i:], B, k - i)
- Else:
- The first j elements of B cannot be the k-th smallest.
- Recursively call
find_kth_smallest(A, B[j:], k - j)
Step 3. Compute the Median:
(The union has
- Find the n-th smallest element m1 using
find_kth_smallest(A, B, n). - Find the
find_kth_smallest(A, B, n + 1). - median = (m1 + m2) / 2
Running time:
- At each recursive call, we reduce the size of the problem by at least half (by
- The number of recursive calls is proportional to
- No merging or linear scans are performed.
- Therefore, the overall time complexity is
中文回答
解答: 我们将使用一个改进的二分搜索算法来查找两个已排序数组并集中的第 k 小元素。关键思想是在每一步都排除掉不可能包含第 k 小元素的那部分数组,从而以对数方式缩小问题规模。
定义函数 find_kth_smallest(A, B, k),其中 A 和 B 是输入数组,k 是所需最小元素的位置。
第1步:基本情况
- 如果一个数组为空:从另一个数组返回第 k 个元素。
- 如果
第2步:递归步骤
- 令
- 令
- 如果
- A 的前 i 个元素不可能是第 k 小的。
- 递归调用
find_kth_smallest(A[i:], B, k - i)
- 否则:
- B 的前 j 个元素不可能是第 k 小的。
- 递归调用
find_kth_smallest(A, B[j:], k - j)
第3步:计算中位数
(并集共有
- 使用
find_kth_smallest(A, B, n)找到第 n 小的元素 m1。 - 使用
find_kth_smallest(A, B, n + 1)找到第 (n+1) 小的元素 m2。 - 中位数 = (m1 + m2) / 2
运行时间:
- 在每次递归调用中,我们将问题规模减小至少一半(减小了
- 递归调用的次数与
- 算法没有执行合并或线性扫描操作。
- 因此,总时间复杂度为
2.贪心:作业二第三题
Question 3 (Optimal Ropes Connection Cost)
English Question
You are given n ropes of different lengths. To connect two ropes, the cost is equal to the sum of their lengths. Your goal is to connect all ropes into a single rope while minimizing the total cost. Design a greedy algorithm to solve this problem.
Input: An array
Output: The minimum total cost to connect all ropes.
Example. Consider the case when we have four ropes, with lengths 2, 3, 4, 6, respectively. To connect these ropes we may have the following two strategies:
- Connect 2 with 3 to form a rope with length 5. Connect 4 with 5 to form a rope with length 9. Connect 6 with 9 to form a rope with length 15. The total cost is
- Connect 4 with 6 to form a rope with length 10. Connect 3 with 10 to form a rope with length 13. Connect 2 with 13 to form a rope with length 15. The total cost is
The first strategy is better as it has lower cost.
中文问题
给定 n 根不同长度的绳子。连接两根绳子的成本等于它们长度的总和。您的目标是将所有绳子连接成一根绳子,同时最小化总成本。设计一个贪心算法来解决这个问题。
输入: 一个数组
输出: 连接所有绳子的最小总成本。
示例: 考虑我们有四根绳子,长度分别为 2, 3, 4, 6 的情况。
连接这些绳子我们可以采用以下两种策略:
- 将 2 和 3 连接,形成长度为 5 的绳子。将 4 和 5 连接,形成长度为 9 的绳子。将 6 和 9 连接,形成长度为 15 的绳子。总成本为
- 将 4 和 6 连接,形成长度为 10 的绳子。将 3 和 10 连接,形成长度为 13 的绳子。将 2 和 13 连接,形成长度为 15 的绳子。总成本为
第一种策略更好,因为它的成本更低。
English Answer
Algorithm Logic: To minimize the total cost of connecting ropes, we must use a Greedy Strategy. The cost of connecting two ropes is the sum of their lengths, which means the length of a rope formed early in the process will be added to the total cost multiple times (once for every subsequent connection it is part of). Therefore, to minimize the total cost, we must ensure that the shortest ropes are merged first and the longest ropes are merged last. This is the exact logic used in Huffman Coding.
Pseudo Code: We use a Min-Priority Queue (Min-Heap) to efficiently access the smallest ropes.
1 | Algorithm ConnectRopes(R) |
Time Complexity:
中文回答
- 算法逻辑
为了最小化连接绳子的总成本,我们必须使用 贪心策略 (Greedy Strategy)。由于连接两根绳子的成本等于它们长度之和,这意味着早期形成的绳子长度会被多次计入总成本(每次后续合并都会包含它)。因此,为了使总成本最小,我们必须确保最短的绳子最先合并,而最长的绳子最后合并。这与 哈夫曼编码 (Huffman Coding) 的逻辑完全一致。
- 伪代码
我们使用最小优先队列(Min-Heap)来高效地获取最小的绳子。
1 | Algorithm ConnectRopes(R) |
时间复杂度:
2.贪心:作业二第四题
Question 4 (Minimum Arrows to Burst Balloons)
English Question
You are given n balloons on a 1D coordinate plane, where each balloon is represented as an interval
Input: A list of intervals
Output: The minimum number of arrows required.
Example. Consider the balloons represented by the following intervals: [2,4], [3, 6], [5, 9], [7, 8]. You may burst all these balloons with the following combinations of arrow shots:
- 2 (burst [2,4]), 5 (burst [3, 6], [5, 9]), 7.5 (burst [7, 8])
- 3 (burst [2, 4], [3, 6]), 7 (burst [5, 9], [7, 8])
The second approach is better as it only requires 2 arrow shots.
中文问题
在一维坐标平面上给定 n 个气球,每个气球由一个区间
输入: 一个区间列表
输出: 所需的最少箭数。
示例: 考虑由以下区间表示的气球:[2,4], [3, 6], [5, 9], [7, 8]。
您可以通过以下射击组合引爆所有这些气球:
- 射击点 2 (引爆 [2,4]), 点 5 (引爆 [3, 6], [5, 9]), 点 7.5 (引爆 [7, 8])
- 射击点 3 (引爆 [2, 4], [3, 6]), 点 7 (引爆 [5, 9], [7, 8])
第二种方法更好,因为它只需要 2 支箭。
English Answer
Algorithm Logic: The goal is to find the minimum number of points (arrows) that intersect all intervals. The optimal greedy strategy is to sort the balloons by their end coordinates (
Pseudo Code
1 | Algorithm BurstBalloons(Intervals) |
Time Complexity: The sorting step dominates the complexity, taking
中文回答
- 算法逻辑
这个问题是 区间调度 (Interval Scheduling) 或 活动选择问题 的一个变体。目标是找到能覆盖所有区间的最小点(箭)数。
最优的贪心策略是根据气球的 结束坐标 (
2. 伪代码
1 | Algorithm BurstBalloons(Intervals) |
时间复杂度: 排序步骤占主导地位,耗时
3.动态规划:作业二第五题
Question 5 (Palindrome Partitioning - Minimum Cuts)
English Question
A palindrome is a sequence of characters that reads the same forward and backward. Examples of palindromes are: "radar", "madam", "level", "a", "I", "abccba", "bbb", etc. Given a string S[1...n], partition it into the minimum number of substrings such that each substring is a palindrome. Design an algorithm to solve this problem using dynamic programming.
Input: A string S.
Output: The minimum number of cuts required to partition S into palindromic substrings.
Example. The following input strings can be divided as follows:
- INPUT: "abcddcbd". OUTPUT: "a|bcddcb|d"
- INPUT: "south". OUTPUT: "s|o|u|t|h"
- INPUT: "banana". OUTPUT: "b|anana" (Note: PDF spelling corrected from 'OTUPUT: blanana')
(1)
①parametrize the problem: Let S[i][j] be the minimum number of cuts,where 1<=i,j<=n. Using j is to present the reverse of S.
②handle the base case: i=j=0
③write a recurrence for large subproblems:
中文问题
回文是指正读和反读都相同的字符序列。回文的例子有:"radar", "madam", "level", "a", "I", "abccba", "bbb" 等。给定一个字符串 S[1...n],将其分割成最少数量的子串,使得每个子串都是回文。设计一个使用动态规划的算法来解决这个问题。
输入: 一个字符串 S。
输出: 将 S 分割成回文子串所需的最少切割次数。
示例: 以下输入字符串可以按如下方式分割:
- 输入: "abcddcbd". 输出: "abcddcb|d"
- 输入: "south". 输出: "s|o|u|t|h"
- 输入: "banana". 输出: "b|anana"
English Answer
Algorithm Logic
This problem requires Dynamic Programming (DP). The solution involves two steps:
- Pre-computation: Create a table
isPal[i][j]that stores whether substring - Min-Cut Calculation: Let
C[i]be the minimum cuts needed for the prefixC[i], we check every possible split pointC[j] + 1). We take the minimum over all valid
Pseudo Code
1 | Algorithm PalindromePartition(S) |
Time Complexity: Building the isPal table takes
C array takes
中文回答
算法逻辑
此问题需要使用动态规划 (Dynamic Programming) 。我们不能使用简单的贪心方法,因为局部最优的回文可能会阻碍全局最优的分割。解决方案包含两个步骤:
- 预计算: 创建一个表
isPal[i][j]来存储子串 - 最小切割计算: 设
C[i]为前缀C[i],我们检查每一个可能的分割点C[j] + 1)。我们在所有有效的
伪代码
1 | Algorithm PalindromePartition(S) |
时间复杂度:构建 isPal 表需要
C 数组需要
AI对话
现在我要开始准备算法分析与设计考试中的一个重点题型“综合设计题”他占20分(满分100),考察形式为题目背景一大段,最后会告诉你请用分治算法(divide and conquer),贪心算法(Greedy Algorithm),动态规划算法(Dynamic Programming)中的一种来解这道题。题目分为几个小问(我不知道会怎么问),但是我猜测(1)问用文字等形式描述解题的过程(比如动态规划就用pdf所示的四个步骤把dp方程推出来,那么观察dp的规律还得画一个二维表来观察,这也是过程,贪心就先像分数背包问题那样按价值比进行排序等)(2)写伪代码(这是一定的,形式就像可见那样先定义Algorithm xxx()然后写INPUT,OUTPUT是什么,然后再具体写伪代码)(3)问时间复杂度(分治就用master theorem,贪心和动归就按循环多少个时间复杂度就是多少来分析)。因此我希望你按照我提供的信息帮我给分治、贪心、动态规划各出三道题来帮助我练手。为了帮助你更好的理解这三道题得出成啥样,我会给你三个案例,你参照着出就行(需要注意我提供的案例并不完全满足我前面提到的考查形式,你需要优先参考考查形式来出题)
首先对于动态规划,四个步骤的写作模式如下:
题目是有些单词看起来相似,而有些单词看起来不同:Whangarei、Wanganui、Auckland
我们能否将这种相似性和差异性的概念形式化?我们能定义单词的距离度量吗?
Edit Distance:两个单词的编辑距离是将一个单词转换为另一个单词所需的最小编辑次数,这里的编辑包括字母的插入、删除和替换。
问题:Given two words
Different ways of aligning the words result in different number of edits.单词的不同对齐方式会导致不同的编辑次数。
The edit distance problem asks for the best way to align the words.编辑距离问题寻求的是对齐单词的最佳方式。
①Parametrize the problem: Divide the problem into subproblems indexed by a parameter:
We compute
②Handle the base case
③Write a recurrence for larger subproblems
④Fill the table of partial solutions in a bottom-up way
Start from $E(0, j) $, then compute
然后伪代码如下:
1 | EditDistance(a[1..m],b[1..n]) |
最后求时间复杂度;
其次对于贪心,题目会类似于:
Knapsack Problem背包问题
INPUT: Values
OUTPUT: A selection of
(1)Local Optimisation Value:At each step, we optimise the
(2)Greedy Choice Property:
Suppose
We make another greedy choice:
①Take the remaining item with highest value/weight ratio, say
②Add
Then the resulting solution $S^{'} $is also a partial optimal solution.那么得到的解S'也是一个部分最优解。
Example W = 100 , w = [20,25,50,40,30, 60] , v = [70,125,80, 80,120, 60] .
Iteration 0: The value-weight ratio set P = {(1, 5), (4, 4), (0, 3.5), (3, 2), (2, 1.6), (5, 1)}, the selection set S = {}, the remaining weight array w′ = [20, 25, 50, 40, 30, 60], the remaining knapsack capacity W' = 100, and the total value TotalValue = 0.
Iteration 1: The value-weight ratio set P = {(4, 4), (0, 3.5), (3, 2), (2, 1.6), (5, 1)}, the selection set S = {(1, 25)}, the remaining weight array w′ = [20, 0, 50, 40, 30, 60], the remaining knapsack capacity W' = 75, and the total value TotalValue = 125.
Iteration 2: The value-weight ratio set P = {(0, 3.5), (3, 2), (2, 1.6), (5, 1)}, the selection set S = {(1, 25), (4, 30)}, the remaining weight array w′ = [20, 0, 50, 40, 0, 60], the remaining knapsack capacity W' = 45, and the total value TotalValue = 125 + 120 = 245.
Iteration 3: The value-weight ratio set P = {(3, 2), (2, 1.6), (5, 1)}, the selection set S = {(1, 25), (4, 30), (0, 20)}, the remaining weight array w' = [0, 0, 50, 40, 0, 60], the remaining knapsack capacity W' = 25, and the total value TotalValue = 245 + 70 = 315.
Iteration 4: The value-weight ratio set P = {(2, 1.6), (5, 1)}, the selection set S = {(1, 25), (4, 30), (0, 20), (3, 25)}, the remaining weight array w' = [0, 0, 50, 15, 0, 60], the remaining knapsack capacity W' = 0, and the total value TotalValue = 315 + 50 = 365.
伪代码如下
1 | Algorithm FracKnapsack(v[1 . . n] , w[1..n], W) |
最后对于递归分治,题目类似于(当然这个题目太短了没有问题背景,是不合格的题目,但是考查形式类似,就是考察排序相关内容):
English Question
Given two sorted arrays of length n, find the median of their union in
中文问题
给定两个长度为 n 的已排序数组,请在
English Answer
Solution: We will use a modified binary search algorithm to find the k-th smallest element in the union of two sorted arrays. 3The key idea is to eliminate parts of the arrays that cannot contain the k-th smallest element at each step, thus reducing the problem size logarithmically. 4
Define function find_kth_smallest(A, B, k) where A and B are the input arrays and k is the position of the desired smallest element. 5
Step 1. Base Cases:
- If one array is empty: Return the k-th element from the other array.
- If
Step 2. Recursive Step:
- Let
- Let
- If
- The first i elements of A cannot be the k-th smallest.
- Recursively call
find_kth_smallest(A[i:], B, k - i)
- Else:
- The first j elements of B cannot be the k-th smallest.
- Recursively call
find_kth_smallest(A, B[j:], k - j)
Step 3. Compute the Median:
(The union has
- Find the n-th smallest element m1 using
find_kth_smallest(A, B, n). - Find the
find_kth_smallest(A, B, n + 1). - median = (m1 + m2) / 2
Running time:
- At each recursive call, we reduce the size of the problem by at least half (by
- The number of recursive calls is proportional to
- No merging or linear scans are performed.
- Therefore, the overall time complexity is
中文回答
解答: 我们将使用一个改进的二分搜索算法来查找两个已排序数组并集中的第 k 小元素。关键思想是在每一步都排除掉不可能包含第 k 小元素的那部分数组,从而以对数方式缩小问题规模。
定义函数 find_kth_smallest(A, B, k),其中 A 和 B 是输入数组,k 是所需最小元素的位置。
第1步:基本情况
- 如果一个数组为空:从另一个数组返回第 k 个元素。
- 如果
第2步:递归步骤
- 令
- 令
- 如果
- A 的前 i 个元素不可能是第 k 小的。
- 递归调用
find_kth_smallest(A[i:], B, k - i)
- 否则:
- B 的前 j 个元素不可能是第 k 小的。
- 递归调用
find_kth_smallest(A, B[j:], k - j)
第3步:计算中位数
(并集共有
- 使用
find_kth_smallest(A, B, n)找到第 n 小的元素 m1。 - 使用
find_kth_smallest(A, B, n + 1)找到第 (n+1) 小的元素 m2。 - 中位数 = (m1 + m2) / 2
运行时间:
- 在每次递归调用中,我们将问题规模减小至少一半(减小了
- 递归调用的次数与
- 算法没有执行合并或线性扫描操作。
- 因此,总时间复杂度为
老师还提供了三种题型的代码模板,我觉得写代码参考这个来挺好:
①动态规划
1 | function() |
②贪心
1 | function() |
③递归分治:
1 | function(n) |
比如说MergeSort的模板对应为:
1 | function MergeSort(list input[0..n-1]) |
比如说QuickSort的模板对应为:
1 | function QuickSort(list a[0..n-1],integer i,integer j) |
你觉得上述内容足够支撑你帮我出题了吗?我希望你给我出动态规划三题,贪心三题,分治两题。因为这些题目和解答肯定很长(而且我要求按照英文题目-英文答案-中文题目-中文答案的形式给出方便我对照着看),所以一个一个来,先给动态规划。等我给下一步指令再到贪心,最后是分治。我要求动态规划至少有一题适合单词相关的,因为作业里也考察了动规,背景也是单词/字符串“English Question
A palindrome is a sequence of characters that reads the same forward and backward. Examples of palindromes are: "radar", "madam", "level", "a", "I", "abccba", "bbb", etc. Given a string S[1...n], partition it into the minimum number of substrings such that each substring is a palindrome. Design an algorithm to solve this problem using dynamic programming.
Input: A string S.
Output: The minimum number of cuts required to partition S into palindromic substrings.
Example. The following input strings can be divided as follows:
- INPUT: "abcddcbd". OUTPUT: "abcddcb|d"
- INPUT: "south". OUTPUT: "s|o|u|t|h"
- INPUT: "banana". OUTPUT: "b|anana" (Note: PDF spelling corrected from 'OTUPUT: blanana')
”此外我还提供了作业题目和答案的pdf。你可以从中汲取出题灵感。阅读上述内容,阅读完告诉我,我同意后就开始出动态规划的题目。
AI出题
动态规划 (Dynamic Programming)
练习题 1:DNA序列比对 (Longest Common Subsequence)
In bioinformatics, a common task is to compare two DNA sequences to determine how similar they are. A DNA sequence is represented as a string consisting of characters 'A', 'C', 'G', 'T'.
Given two DNA sequences
Input: Two strings
Output: The length of the longest common subsequence of
Example
-
INPUT:
-
OUTPUT: 2
Explanation: The longest common subsequences are "GC" or "GA" or "AC". Length is 2.
(1) Describe the solution process (Parametrize, Base case, Recurrence, Table filling).
(2) Write the pseudocode.
(3) Analyze the time complexity.
(1) Solution Process
-
Parametrize the problem:
We define a 2-dimensional array
Let
-
Handle the base case:
If either sequence is empty, the LCS length is 0.
-
Write a recurrence for larger subproblems:
We consider the last characters
-
If
-
If
-
-
Fill the table of partial solutions in a bottom-up way:
We iterate
(2) Pseudocode
1 | Algorithm LCS(X[1..m], Y[1..n]) |
(3) Time Complexity
The algorithm uses two nested loops. The outer loop runs
Question 2 (Maximum Weight Independent Set)
You are a professional treasure hunter exploring an ancient dungeon corridor. The corridor contains a sequence of
However, the dungeon is protected by a "Proximity Alarm System". This system is triggered if any two adjacent chests are opened. If the alarm triggers, the dungeon collapses, and you lose all the gold. For example, if you choose to open chest
Your goal is to formulate a strategy to select a subset of chests to maximize the total value of gold collected without triggering the alarm. This is formally known as the Maximum Weight Independent Set problem on a path graph.
Input: An array
Output: The maximum amount of gold that can be collected.
Example:
- Input:
- Output: 12
- Explanation: The optimal strategy is to pick chest 1 (value 2), chest 3 (value 9), and chest 5 (value 1). Total =
(1) Describe the solution process (Parametrize, Base case, Recurrence, Table filling).
(2) Write the pseudocode.
(3) Analyze the time complexity.
贪心算法 (Greedy Algorithm)
Question 1 (The Master Potion Brewer - Fractional Knapsack Variant)
You are a master alchemist competing in a potion-brewing championship. You need to brew a "Universal Elixir" in a cauldron that has a fixed maximum volume capacity of
You have access to
To maximize your score, you want to fill your cauldron with a mixture of ingredients such that the total magical potency is maximized. You can pour any fraction (any amount up to
Input:
- Arrays
- The cauldron's capacity
Output: The maximum total potency you can achieve.
Example:
- Input:
-
-
-
-
(1) Describe the greedy strategy (Logic/Justification).
(2) Write the pseudocode using the provided template.
(3) Analyze the time complexity.
(1) Algorithm Logic
Greedy Strategy: Select ingredients with the highest potency-per-liter ratio (
Justification: Since we can take fractions, filling the limited capacity with the highest density ingredients yields the maximum total value.
- Calculate ratio
- Sort ingredients by
- Iterate and take as much as possible until full.
(2) Pseudocode
1 | Algorithm MaxPotency(p[1..n], l[1..n], V) |
(3) Time Complexity
Calculating ratios takes
Question 2 (Activity Selection Problem)
You are managing a large lecture hall. There are
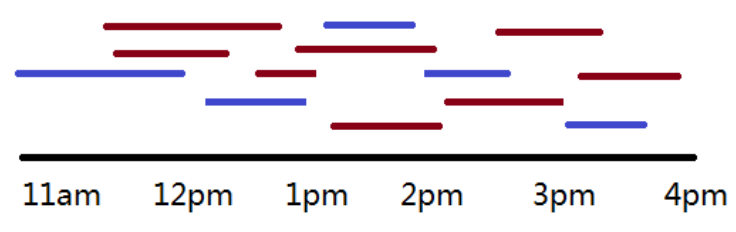
Two activities are compatible if their time intervals do not overlap. Your goal is to select the maximum number of mutually compatible activities to maximize the hall's usage.
(This is the classic Interval Scheduling problem).
Input: Two arrays
Output: The maximum number of activities.
Example:
- Input:
-
-
- (Note: Each pair
-
(1) Describe the greedy strategy (Logic/Justification).
(2) Write the pseudocode using the provided template.
(3) Analyze the time complexity.
Question 3 (Huffman Coding - Data Compression)
In data transmission and storage, we want to represent characters using binary codes (sequences of 0s and 1s) such that the total length of the encoded message is minimized.
Given a file containing
This problem is solved by constructing a Huffman Tree. The logic builds the tree bottom-up by repeatedly merging the two least frequent characters.
Input: An array of characters
Output: The root of the Huffman Tree.
Example:
- Input:
-
-
-
(1) Describe the greedy strategy (Logic/Justification).
(2) Write the pseudocode using the provided template.
(3) Analyze the time complexity.
递归分治 (Divide and Conquer)
当你拿到一道新题,想用分治法时,问自己一个问题:
“左右两部分的结果,是否相互独立?”
情况 A:如果不独立(需要发生关系)
- 例子:逆序对(左边的大数和右边的小数组成逆序对)、最大子数组(左后缀和右前缀连起来)。
- 策略:不管左右(相信递归),只管中间(写一个
Cross或Merge函数)。 - 代码位置:写在递归调用之后。
情况 B:如果在处理前就能让它们独立
- 例子:快速排序(小的全去左边,大的全去右边,老死不相往来)。
- 策略:先大力出奇迹(Partition),把数据物理隔绝开,然后递归。没有中间环节。
- 代码位置:写在递归调用之前。
情况 C:最极端的“只选一边”
- 例子:二分查找 (Binary Search)。
- 策略:切一刀,发现目标肯定在左边,那右边直接扔掉。
- 特点:既不需要 Divide 的复杂操作,也不需要 Combine,只需要选择。
练习题 1:逆序对计数 (Counting Inversions)
A music streaming platform wants to compare the musical tastes of two users. They represent each user's preference as a ranked list of
An inversion is a pair of indices
Design a divide-and-conquer algorithm to count the total number of inversions in an array
Input: An array
Output: The number of inversions in
Example
INPUT:
OUTPUT: 3
(Explanation: The inversions are
(1) Describe the divide-and-conquer strategy.
(2) Write the pseudocode using the provided template.
(3) Analyze the time complexity.
(1) Algorithm Logic
Strategy: Modify the Merge Sort algorithm.
Divide: Partition the array
Conquer: Recursively count inversions in the left subarray and the right subarray.
Combine: Count the split inversions (where
Result:
(2) Pseudocode
1 | function CountInversions(array A, integer p, integer r) |
(3) Time Complexity
The recurrence is
MergeAndCount procedure (linear scan). By the Master Theorem,
练习题 2:最大子数组问题 (Maximum Subarray Problem)
You are analyzing the daily stock price changes of a company over a period of
Design a divide-and-conquer algorithm to solve this problem.
Input: An array
Output: The maximum sum of any contiguous subarray in
Example
INPUT:
OUTPUT: 6
(Explanation: The contiguous subarray
(1) Describe the divide-and-conquer strategy.
(2) Write the pseudocode using the provided template.
(3) Analyze the time complexity.
(1) Algorithm Logic
Strategy: Divide the array into two equal halves. The maximum subarray must be located in one of three places:
- Entirely in the left half
- Entirely in the right half
- Crossing the midpoint
Conquer: Recursively find the max subarray sum in the left and right halves.
Combine: Find the max crossing subarray sum. Extend from the midpoint to the left to find the max left-suffix, and extend to the right to find the max right-prefix, then sum them (
Result: Return
(2) Pseudocode
1 | function FindMaxSubarray(array A, integer p, integer r) |
(3) Time Complexity
The FindMaxCrossingSubarray function takes