数据分析方法

发表于 2025-03-03 更新于 2026-01-09 分类于学习阅读次数：

| 置顶

本文字数： 931k 阅读时长 ≈ 28:12

数据分析方法

Date：2025.12.22 23:19

[toc]

说在课前

1.读表格/读数据

1 2	> ## Importing data from R > Stata20x.df = read.table("Data/STATS20x.txt",header=TRUE)

2.画直方图

1 2	> #Using xlab="STATS 20x exam score" to label the x-axis > hist(Stats20x.df$Exam, xlab="STATS 20x exam score")

3.散点图

> ##Importing data into R
> Stats20x.df = read.table("Data/STATS20x.txt",header=T/TRUE)
> ##Plot the data
> plot(Exam ~ Test, data =Stats20x.df)//画散点图

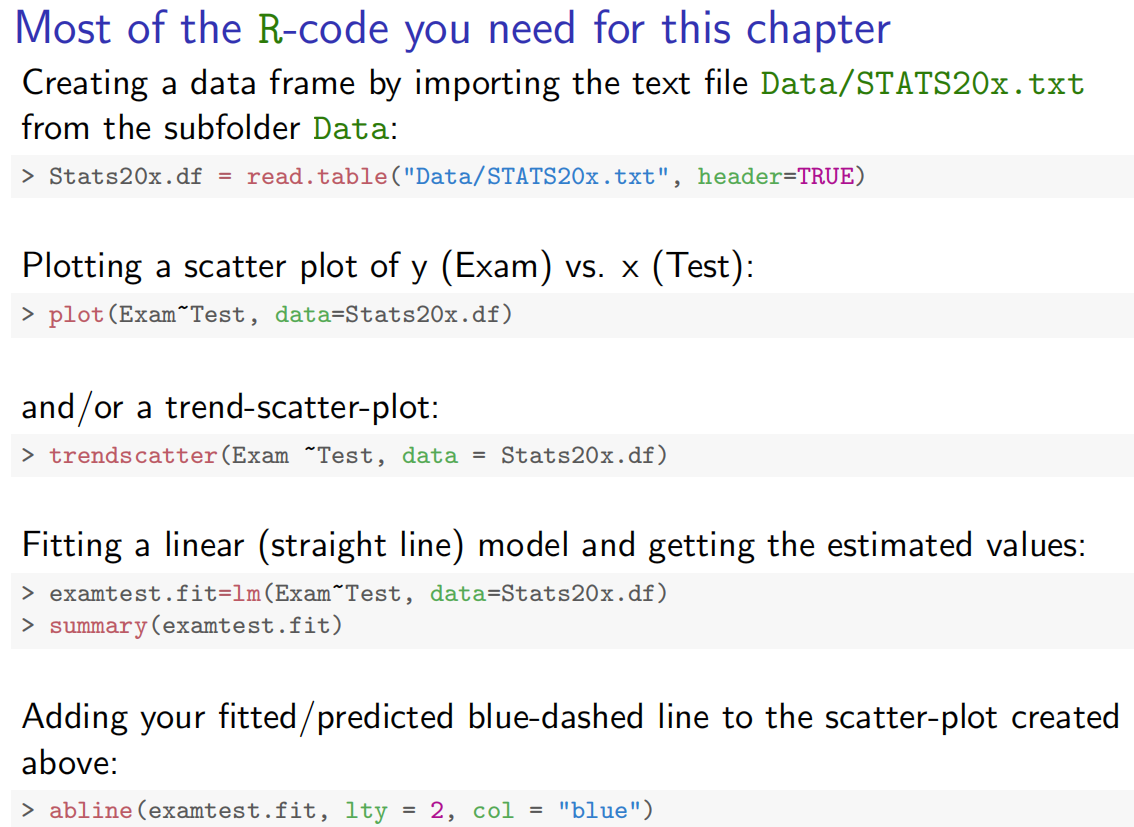
Note that the plot(Exam ~ Test, data = Stats20x.df) statement asks R to produce a plot suitable for showing how Test(x-axis variable) is related to Exam(y-axis variable)

请注意，plot(Exam ~ Test, data = Stats20x.df) 这条语句要求 R 语言生成一个适合展示 “测试（横轴变量）” 与 “考试（纵轴变量）” 之间关系的图表。

4.查维度

1
2
3

> dim(Stats20x.df)

[1] 146 15

5.查具体dataframe内容

1
2
3

> Stats20x.df$Exam[1:10]

[1]42 58 ......

$ after dataframe name to ask for one variable

在数据框名称后面使用 $ 符号来提取其中的一个变量

5.预测

> examtest.fit = lm(Exam ~ test, data = Stats20x.df)
> summary(examtest.fit)//用test预测exam
> preds.df <- data.frame(Test = c(0,10,20))
> predict(examtest.fit, preds.df, interval="confidence")

点估计 $\hat{Y}$

     1(0分)      2(10分)     3(20分)--半期对应Test = c(0,10,20)
   9.084463   46.943703   84.802942 --期末

> # we would like to know the reliability of the above estimates. That is
> # easy-just ask for their confidence interval:
我们想了解上述估计值可靠性。这很简单——只需获取它们的置信区间即可：
> predict(examtest.fit, preds.df, interval="confidence")

        fit         lwr         upr
1  9.084463     2.71902    15.44991
2               ......
3               ......

另一样本均值有95%概率落在lwr,upr之间

fit就是(lwr,upr)/2，代表“半期为x分的这些同学的期末均值”

> # It may also be of interest to ask for an interval that predicts the Exam
> # score for a single student (rather than an interval for the expected score, as done above). This is also easy-just ask for a prediction interval instead:
或许我们也会对预测单个学生考试成绩的区间感兴趣（而不是像上面那样求预期成绩的区间）。这也很简单 —— 只需改为求预测区间即可：
> predict(examtest.fit, preds.df, interval="prediction")

        fit         lwr         upr
1  9.084463   -15.56475    33.73368
2               ......
3               ......

对于每个人而言（个体）有95%的概率落在lwr-upr之间

==两个预测区别就是一个选择interval=“confidence”，一个选择interval=“prediction”，相对应的，confidence求的是总体均值的置信区间，而prediction求的是个体取值的置信区间。==下面是AI的解释：

在 R 语言中使用 predict 函数时：

当 interval = "confidence" 时，计算的是给定解释变量取值下，响应变量总体均值的置信区间。它反映的是基于样本数据对总体均值的估计范围，体现了总体均值的不确定性。例如，对于一组特定的测试成绩（解释变量），我们想知道对应的考试成绩（响应变量）总体均值大概在什么范围。

当 interval = "prediction" 时，计算的是给定解释变量取值下，单个新观测值的预测区间。它考虑了总体均值的不确定性以及单个观测值围绕总体均值的变异性，所以预测区间通常比置信区间更宽。例如，对于一个特定学生的测试成绩，我们想预测这个学生的考试成绩大概在什么范围。

这两个选项导致不同结果的原因主要在于它们所考虑的不确定性来源不同：

置信区间（interval = "confidence"）

主要关注的是总体回归直线的不确定性。它基于样本数据来估计总体回归模型的参数，由于样本只是总体的一部分，所以参数估计存在一定的误差。置信区间通过考虑这种参数估计的误差，给出总体均值可能的取值范围。其计算主要依赖于回归模型的标准误差以及样本量等因素，用于描述总体均值的可信范围。

预测区间（interval = "prediction"）

除了要考虑总体回归直线的不确定性（即参数估计的误差）外，还要考虑单个观测值偏离总体均值的随机误差。因为即使我们准确知道总体回归直线，单个观测值也会因为各种随机因素而偏离总体均值。所以预测区间要包含这两部分的不确定性，从而比置信区间更宽，以确保能够合理地预测单个新观测值的可能取值。

6.求某点的残差和拟合值 $\hat{y}$

1 2	> resid(examtest.fit)[21] > fitted(examtest.fit)[21]

6.针对该问题的其他可画的图

> plot(Exam~Test, data = Stats20x.df, xlim = c(0,20))
> ## Add the lm estimated line to this plot
> abline(examtest.fit, lty = 2, clo = "blue")//ltm是线粗细
> ## Calculate predicted values for students who get test=0,10,20
> predns = predict(examtest.fit, newdata = data.frame(Test=c(0,10,20)))
> ## Add the predicted values to the plot
> points(c(0,10,20), predns,col = "blue", pch = 19)

总体来看就是绘制散点图、添加线性回归直线、计算预测值、在图中添加预测点

重点：Read in and inspect the data; Comment on the plot; Fit model and check assumption/读取并检查数据；对图表进行评价；拟合模型并检验假设

模型能用吗？ ———> 同分布，正太，异常点

|

|能

↓

summary( ___.fit )

confint( ___.fit ) ———> $β_{0}, β_{1}$

|

|

↓

预测

summary（）：求参数的 $p - v a l u e$ , $R^{2}$

confint（）：判断拟合参数的置信区间

7.检验模型是否可行

同分布

plot(**.fit, which=1)

使用 lm() 函数拟合线性回归模型后，plot() 函数可以用来绘制多种与模型诊断相关的图形。which = 1 表示绘制残差与拟合值的散点图。

如果残差随机地分布在零水平线附近，且在不同拟合值处的残差散布范围大致相同，就表明残差可能具有同方差性，也就是满足同分布的一个重要方面；若残差呈现出喇叭状或者其他有规律的分布，那就可能存在异方差问题。

trendscatter(....)

trendscatter() 函数来自 lattice 包，用于绘制散点图并添加平滑曲线。

在模型诊断的情境下，通常是对残差和某个自变量或者拟合值绘制散点图，并添加平滑曲线，以此来帮助识别残差中可能存在的趋势。

如果平滑曲线是接近水平的，说明残差没有明显的趋势，这与同分布的假设相符；若曲线有明显的上升或下降趋势，就可能暗示模型存在问题，比如遗漏了重要的自变量。

代码中的省略号需要替换为实际的数据参数，例如 trendscatter(x, y)，这里 x 可以是拟合值，y 是残差。

正态分布

normcheck()

用于检查数据或者模型残差是否服从正态分布。

可能会绘制正态概率图（QQ 图），在图中如果数据点大致沿着一条直线分布，就说明数据或者残差近似服从正态分布。此外，它可能还会进行一些正态性检验，如 Shapiro - Wilk 检验等，根据检验的 p 值来判断是否拒绝正态分布的原假设。

是否有异常点

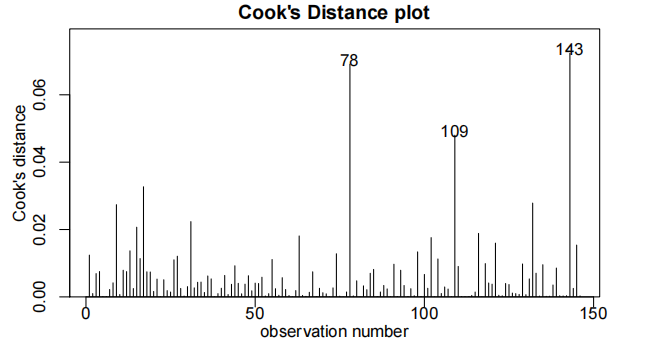
cooks20x()

在回归分析中，Cook's 距离是一种用于衡量每个数据点对回归模型影响的指标。Cook's 距离较大的数据点可能是异常点，因为它们对回归系数的估计有较大的影响。cooks20x() 可能是一个自定义函数或者来自某个特定包的函数，其作用可能是计算并展示 Cook's 距离，帮助识别数据集中的异常点。

> # fit the model
> fire.fit<-lm(damage~distance,data=fire.df)
> plot(examtest.fit, which = 1)
> trendscatter(Exam~Test, data = Stats20x.df)
> normcheck(examtest.fit)
> cooks20x(examtest.fit)

8.从拟合模型中得出一些结论

$β_{0}, β_{1}$ 的区间估计
对于具体的 $X$ 进行总体（均值）估计和个体估计

点估计，均值估计，个体估计

predict( , )：点估计。当使用 predict 函数且不指定 interval 参数时，它返回的是点估计值。

predict(model, newdata)如果我们有一个线性回归模型用于预测学生的考试成绩（因变量）与学习时间（自变量）的关系，给定一个新的学习时间值，predict 函数会输出一个具体的考试成绩预测值。

predict( , , interval = "confidence")：均值估计。当指定 interval = "confidence" 时，predict 函数会计算并返回置信区间，这里的置信区间是针对总体均值的。

假设学习时间为 5 小时，返回的置信区间为 [70, 80]，这意味着我们有 95% 的把握认为所有学习 5 小时的学生的平均考试成绩在 70 到 80 分之间。

predict( , , interval = "prediction")：个体估计。当指定 interval = "prediction" 时，predict 函数会计算预测区间。预测区间是针对单个新观测值的，它考虑了总体均值的不确定性以及个体观测值围绕总体均值的变异性。

同样对于学习时间为 5 小时的情况，预测区间可能会比置信区间更宽，比如 [60, 90]，这表示我们有 95% 的把握认为一个新的学习 5 小时的学生的考试成绩会在 60 到 90 分之间。

> # Get additonal predicted output
> predict( , )
> predict( , , interval = "confidence")
> predict( , , interval = "prediction")

1	> confint(examtest.fit)

1
2
3

                   2.5%     97.5% 
β0(Intercept)  2.719020 15.449907
β1 Test        3.262659  4.309189

$β_{0}$ 的值有95%概率在(2.72,15.45)

$β_{1}$ 的值由95%概率在(3.26,4.31)

1	> confint(examtest.fit,level=0.99)

1
2
3

                   0.5%     99.5% 
β0(Intercept)          ......
β1 Test                ......

level 参数指定了置信区间的置信水平，它是一个介于 0 和 1 之间的数值。在上述代码中，level = 0.99 表示计算的是 99% 的置信区间。

9.Method and Assumption Checks/方法和假设检验

描述数据和你为什么选择这个模型
这个拟合模型的假设检验怎样？
拟合线性方程（需要特别注明的假设：残差的假设）
our model explains ***% of the variation……(R方)/我们的模型解释了……% 的变异……（R 方）

1
2
3

> # plot with superimposed line带有叠加直线的绘图
> plot(price~weight,main="Price versus weight of diamonds",data=diamonds.df)
> abline(diamond.fit$coef[1],diamond.fit$coef[2])

10.Executive Summary内容提要

重点两部分

拟合模型的参数的区间估计的含义的描述
回答题目中提出的问题

11.Data Analysis

环境的准备

R, R-Studio, R-markdown, Package:S20x, library(S20x)

数据分析的过程

（1）读问题 -到底要解决什么？预测什么？

（2）看数据 -plot（）形状，趋势

（3）试拟合 -lm

（4）判拟合 -假设检验（iid，异常数据），summary（参数的 $p - v a l u e$ , $R^{2}$ ）,如果不接受这个结果，转（3）

（5）画拟合 -plot abline

（6）看参数 -判断拟合参数的置信区间 confint（）

（7）做预测 -题目中给出的数据进行点估计（个体取值估计），区间估计（总体均值估计）predict（）

（8）做总结 -方法的总结，数据的总结

Chapter1: Getting started with linear regression

见说在课前，主要讲了：

读数据：Stats20x.df = read.table("Data/STATS20x.txt", header=TRUE)
查看数据结构：Stats20x.df[1:5,1:7]

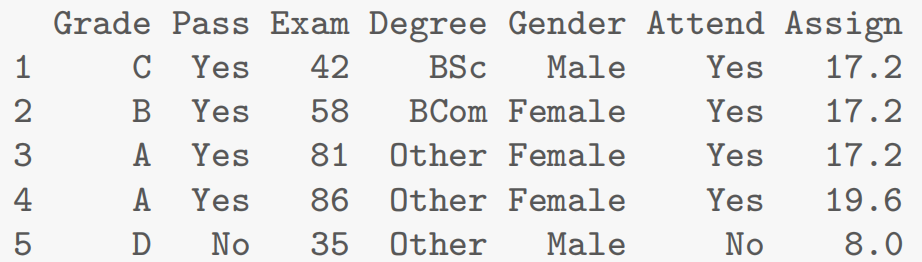
查看数据维度（表格的行列数）：dim(Stats20x.df)

只查看具体一列（如Figure 1中的exam）：Stats20x.df$Exam[1:10]

查看数值总结（如最值、分位数、均值）：summary(Stats20x.df$Exam)

注意：对lm也就是线性回归后的变量进行summary输出的结果与对某一列不尽相同，如：
1
2
> examtest.fit = lm(Exam ~ Test, data = Stats20x.df)
> summary(examtest.fit)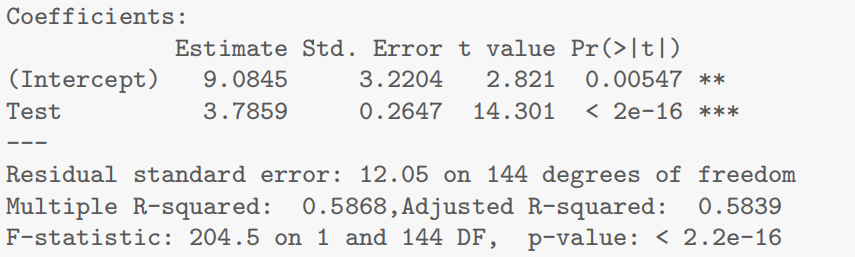
描点：plot(Exam ~ Test, data = Stats20x.df)
平滑趋势线绘制(s20x独有）：trendscatter(Exam ~ Test, data = Stats20x.df)

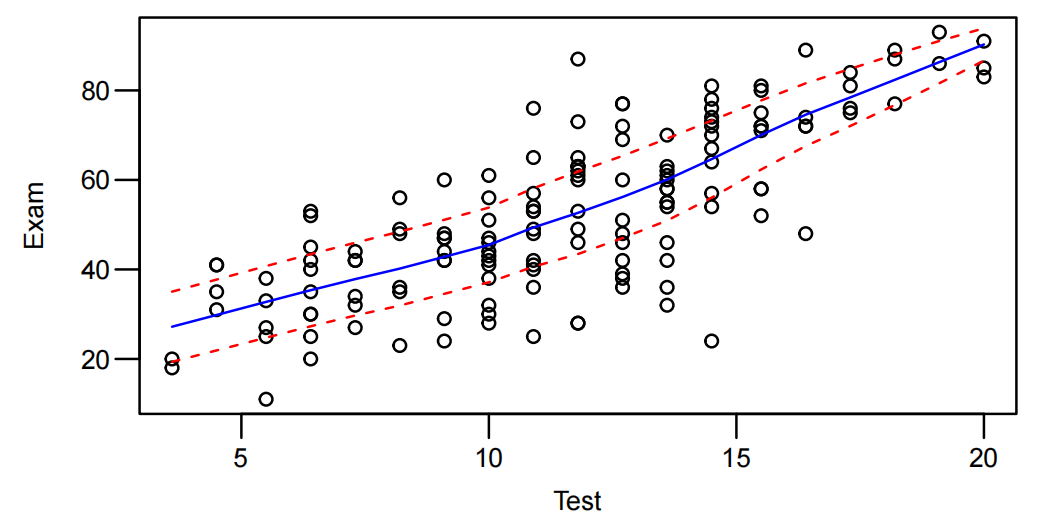
查看拟合数据：coef(examtest.fit)

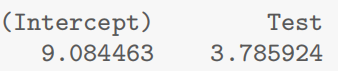
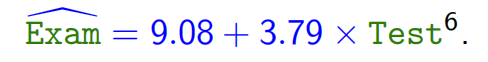
Chapter2: The basics of simple linear regression

查看特定点拟合数据fitted(examtest.fit)[21]

查看特定点残差情况resid(examtest.fit)[21]

残差计算公式（对于该点） $r_{21} = y_{21} - {\hat{y}}_{21} = 77 - 57.1657 = 19.8343$

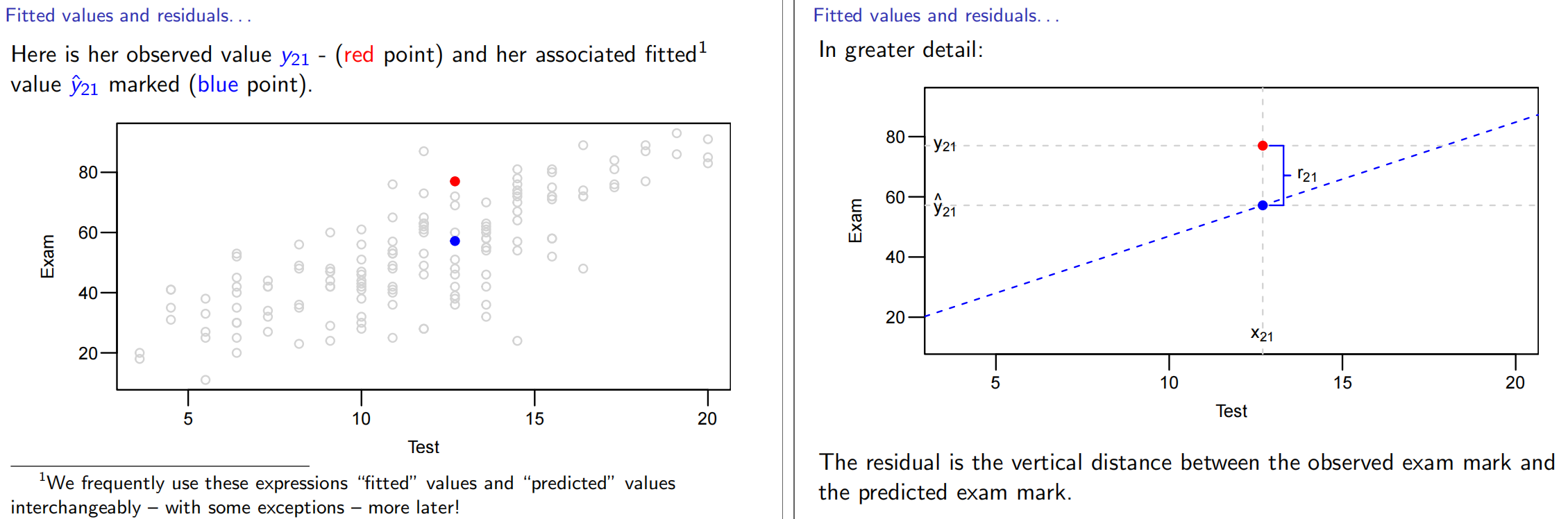
最小二乘法least squares算 $\hat{β_{0}}$ 及 $\hat{β_{1}}$

$\sum {r_{i}}^{2} = \sum (y_{i} - \hat{β_{0}} - \hat{β_{1}} x_{i})^{2} = m i n \sum {ϵ_{i}}^{2} = \sum (y_{i} - β_{0} - β_{1} x_{i})^{2}$

通过用拟合后曲线与原数据点做残差平方和，可以发现拟合后曲线残差减少了59%。 $R^{2} = 1 - \frac{r e s i d_{l m}}{r e s i d_{n u l l}} = 1 - \frac{20901.08}{50585.78} = 0.59$

所有线性模型的一般假设

独立：每一个观察结果都独立于其他结果

同分布（EOV： equality of variance）：residual残差 $ε_{i}$ 必须来自相同的、均值为0的、方差相同的分布

正态分布：residual残差 $ε_{i}$ 必须（至少近似）服从正态分布

检验同分布：normcheck(examtest.fit)

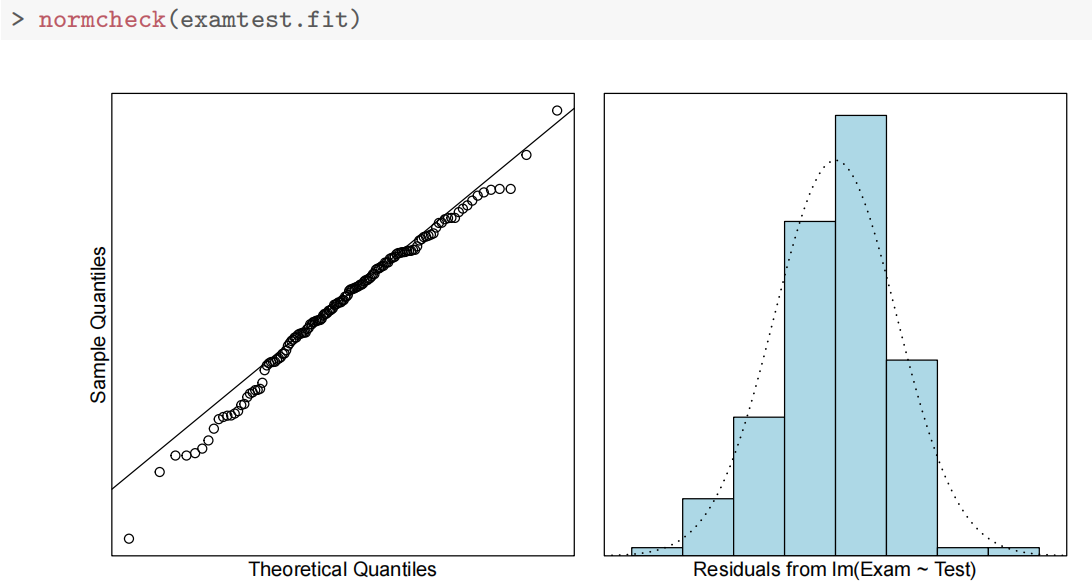
normcheck函数（通常来自nortest包）用于绘制正态性检验的 QQ 图（Quantile-Quantile Plot），并结合统计检验判断数据是否服从正态分布。

QQ图的核心是比较样本分位数与理论正态分布分位数的一致性：

也就是说通过取分位数上点与理论上能让正态分布成立的两个值构成点，看该点是否在对角线，也就是看实际值是否尽可能符合正态分布成立的理论值

理想情况（正态分布）

图中数据点大致分布在一条直线上（直线为参考线，通常由最小二乘法拟合）。

点越贴近直线，数据越接近正态分布。

查看异常点/强影响点：cooks20x(examtest.fit2)：教材中提到参考值是0.4（可根据实际变化，但考试取这个就行）有点>0.4就能说明该点是强影响点

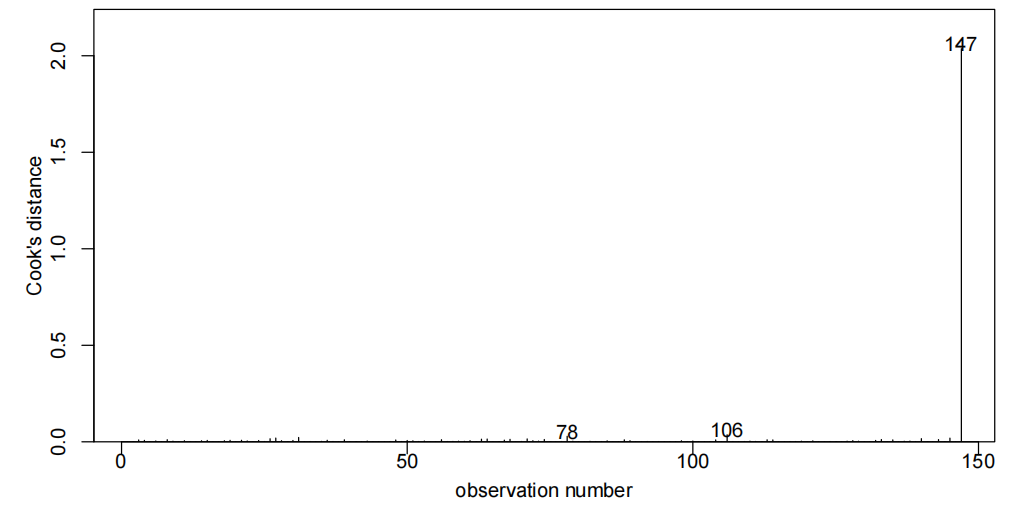
这个图中点147就是有问题的

t-检验成立于线性模型： ${\hat{β}}_{0}$ 和 ${\hat{β}}_{1}$ 都服从正态分布，期望值1为 $β_{0}$ 和 $β_{1}$ ，这意味着仍然可以用标准的统计方法推断正态分布的数据。因此t-statistic用于检验假设，t-multiplier用于构建置信区间和预测区间

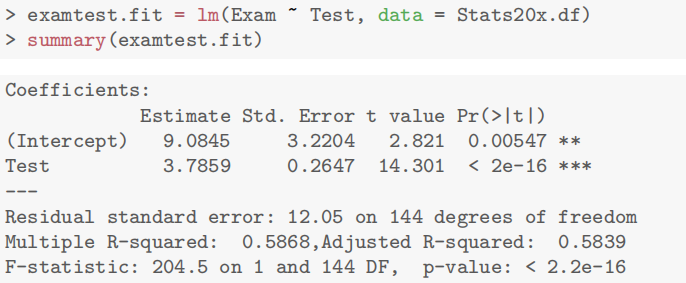
解读：

可以看到对于Test的 $P r < 2 e - 16$ ，通常这个值小到可以被认为是0

t value的由来

$H_{0}$ ：Test和Exam成绩没有关系

那对于 $H_{0}$ 来说， $β_{1}$ 也就是一次项就是0， $y = β_{0} + ε$ 。而 $β_{1}$ 的估计值 ${\hat{β}}_{1} = 3.37859$ （估计值代码里面就是求mean均值）。接下来可以得到 ${\hat{β}}_{1}$ 的标准差为 $s e ({\hat{β}}_{1}) = 0.2641$ 。

$t - v a l u e = \frac{{\hat{β}}_{1} - β_{1}}{s e ({\hat{β}}_{1})} = \frac{3.37859 - 0}{0.2641} = 14.301$

这里的 t 值表示：在零假设成立的前提下，估计系数 ${\hat{β}}_{1}$ 距离零假设值（0）有 14.301 个标准误的差距。

t 值的绝对值越大，说明估计系数与零假设值的差异越 “极端”，即数据提供的 反对零假设的证据越强。

在大样本下，t 分布近似正态分布。因此，t 值可以理解为 “估计系数相对于零假设值的标准差倍数”。例如：

(t = 1.96)（对应 95% 置信水平）：表示估计系数在零假设值的 1.96 个标准误之外，此时拒绝 $H_{0}$ 的概率为 5%。

本例中 (t = 14.301)，远超过常见阈值（如 1.96 或 2.58），说明差异极其显著。

t 值的最终目的是计算 p 值，即 “在零假设成立时，观察到当前或更极端结果的概率”。通过 t 分布表或软件计算 p 值。

求 $β_{1}$ 置信区间（ $β_{0}$ 有需要也可以求）：confint(examtest.fit,level=___)

level=___不写默认是求2.5%到97.5%，写了比如level=0.99就是0.5%-99.5%

confidence intervals用于系数和拟合值（观察整体情况）而prediction interals用于个体预测

对于整体情况：

predict(examtest.fit,preds.df,interval="confidence")

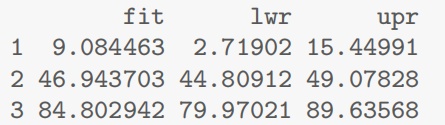
对于单个学生：

predict(examtest.fit,preds.df,interval="prediction")

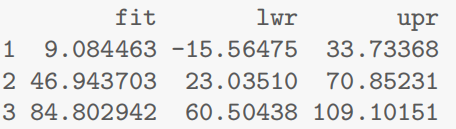
可以发现个体的区间通常是比整体更宽甚至有预测结果是小于0大于100的，说明：

我们已经达到了这个线性模型近似的极限，在预测个体时虽然解释了趋势但是效果其实是变差了，因为前面提到 $R^{2} = 0.59$ 也就是说该模型只能解释总体变化的59%。而在考试的顶端学生通常更少，由于考试分数必须在0到100之间，在数据的这一端可能会有不同的动态，不能仅根据学生的考试分数就给他们一个考试分数。理想情况下，我们希望通过使用额外感兴趣的变量来解释更多的可变性——这被称为多重（而不是简单的）线性回归。

解题套路

1.绘制数据（描点plot）看看有没有什么直观关系，提出一个合适模型。

如第二章主要使用： $y_{i} = β_{0} + β_{1} x_{i} + ε_{i}, ε_{i} \overset{iid}{\sim} N (0, σ^{2}) (where β_{1} > 0.)$

其中 $i i d$ 代表Independent and Identically Distributed 的缩写，中文译为 “独立同分布”

2.用lm线性拟合模型

3.检查独立同分布是否成立。

①首先独立Independence（主要观察数据如何收集，是否合理）

②其次同分布 $E O V$ 是否可以：描点plot(examtest.fit,which=1)看数据点是否上下均匀分布；正态检验normcheck

4.适当情况下删除任何不重要解释变量，随后更新模型（后面介绍）

5.检查是否有异常点强影响点：cooks20x（并去除）

6.得出结论/预测，讨论局限性，并回答相关研究问题。

注意上述步骤不能跳步，必须要都满足才能往下进行

第二章R语言代码总结

主要部分

1.拟合线性模型（直线）

examtest.fit=lm(Exam~test,data=Stats20x.df)

注意：独立性是通过调查数据如何收集来评估

2.检查同分布情况 $E O V$

plot(examtest.fit,which=1)

3.检查是否正态分布

normcheck(examtesy.fit)

4.检查是否有异常点/强影响点

cooks20x(examtest.fit)

其他必要代码

1.评估拟合模型的相关情况

summary(examtest.fit)

2.求模型参数的置信区间（斜率slope和截距intercept）

confint(examtest.fit)

3.对新变量创建一个数据框架data frame（例如，Test=0，10，20）

preds.df=data.frame(Test=c(0,10,20))

4.求新观察的期望值（整体情况）和预测区间（个体情况）的置信区间

Case Study 2.1: Exam vs Test

Problem

我们希望量化测试分数和考试成绩之间的关系，特别是为了能够用他们的测试分数来预测学生的考试分数（帮助没有参加考试的学生决定考试成绩）。特别是，我们想要预测一个学生的考试分数是0、10或20时的考试分数。我们感兴趣的变量是：考试：考试成绩，满分100分。测试：测试标记为20分。

Question of Interest

我们想建立一个模型来预测考试分数的考试分数。特别地，我们想预测一个学生的期末成绩exam当他们的测试成绩test为0，10或20.

Read in and Inspect（检查） the Data

Stats20x.df=read.table("STATS20x.txt",header=T)

plot(Exam~Test,data=Stats20x.df)

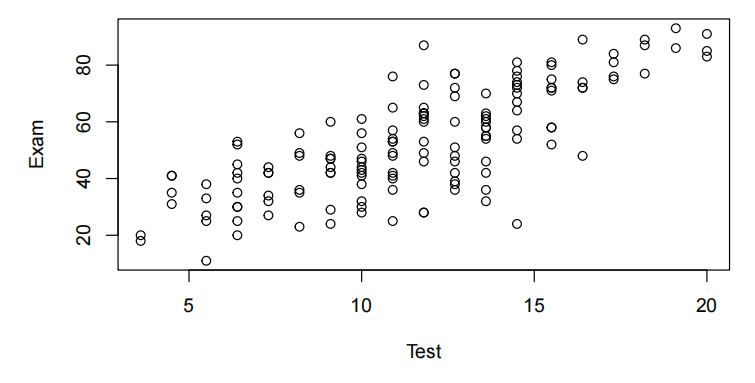
该图（plot）显示（reveal）了考试分数和考试分数之间的正线性关系（a positive linear relationship）。

Model Building and Check Assumptions

examTest.fit=lm(Exam~Test,data=Stats20x.df)

plot(examTest.fit,which=1)

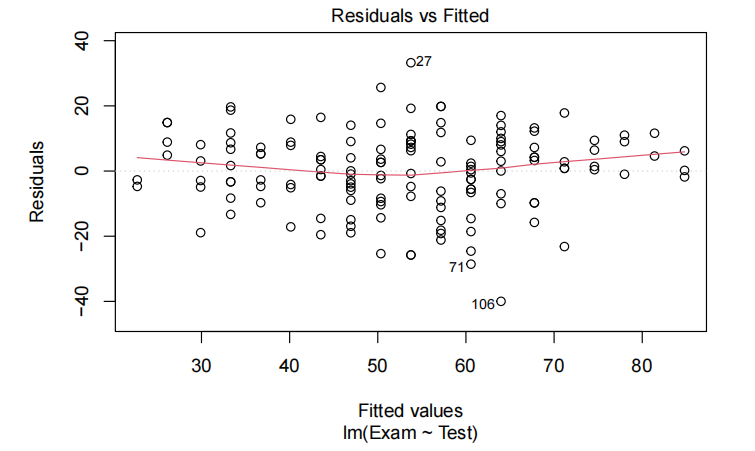
normchek(examTest.fit)

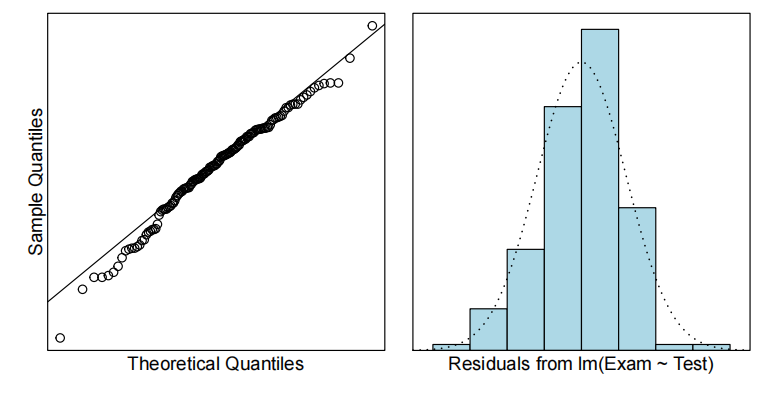
cooks20x(examTest.fit)

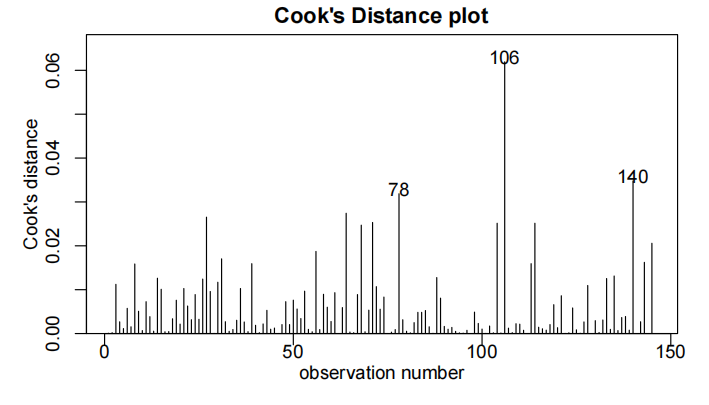
summary(examTest.fit)

confint(examTest.fit)

Prediction Output

predTest.df=data.frame(Test=c(0,10,20))

predict(examTest.fit,predTest.df,interval="prediction")

Method and Assumption Checks

考试分数与测试分数的散点图显示出近似恒定散点的线性关联，因此拟合了一个线性模型。

所有的模型假设似乎都满足了——虽然说在残差图中残差曲线被观察到一个轻微的趋势而不是在0这条线，但似乎不是主要的问题（影响不大）。因此最终模型为： $E x a m_{i} = β_{0} + β_{1} \times T e s t_{i} + ε_{i}$ ，在这里(p35)

对线性模型（如 lm 拟合结果）使用 plot() 函数时，which = 1 用于指定生成残差 vs 拟合值图（Residuals vs Fitted plot）

检验线性假设：观察残差是否随机分布在 0 线附近，若残差呈现明显规律（如曲线形态），可能说明变量间非线性关系未被模型捕捉。

检验同方差性：检查残差的离散程度是否随拟合值变化。若残差扩散程度逐渐变大 / 变小（如漏斗状），可能存在异方差问题。

此外，

which = 2：正态 Q-Q 图，检验残差是否服从正态分布；

which = 3：位置尺度图，进一步分析异方差；

which = 4：残差 vs 杠杆值图，识别高杠杆点。

Executive Summary

我们感兴趣的是建立一个根据测试成绩预测期末成绩的模型。

测试成绩和期末成绩之间存在一个显著的线性关系（significant linear relationship）（P-value≈0）。我们估计学生测试成绩提升一分（20分），他们的期末成绩平均提升3.3-4.3分（100分）。

对于0，10，20的考试成绩，我们预测（学生个人的期末成绩）分别在-15.6-33.7，23.0-70.9和60.5-109.1之间，这些间隔是非常宽的，其中一些间隔的界限已经超出了考试成绩（0-100）的可行值，说明该模型预测结果不可靠。

Case Study 2.2: Fire Damage

Problem

保险公司希望预测如果发生火灾，特定地区房屋损坏的修理成本（约合000美元）。在感兴趣的区域内随机抽取15起房屋火灾样本，记录了损失和距离消防站的距离。他们还特别感兴趣的是预测距离消防站1英里和4英里的房子的火灾损坏的修复成本。

测量的变量为：损坏：损坏修复成本（000美元）距离：距离消防站的距离（以英里为单位）

Question of interest/goal of the study

我们感兴趣的是预测火灾对房屋造成的损失成本，这取决于房屋距离最近的消防站有多远。特别是，我们想要预测距离消防站1英里和4英里的随机选择的房屋的损失成本。

Read in and inspect the data:

fire.df=read.table("fire.txt",header=T)

plot(damage~distance,main="Cost of damage versus distance",data=fire.df)

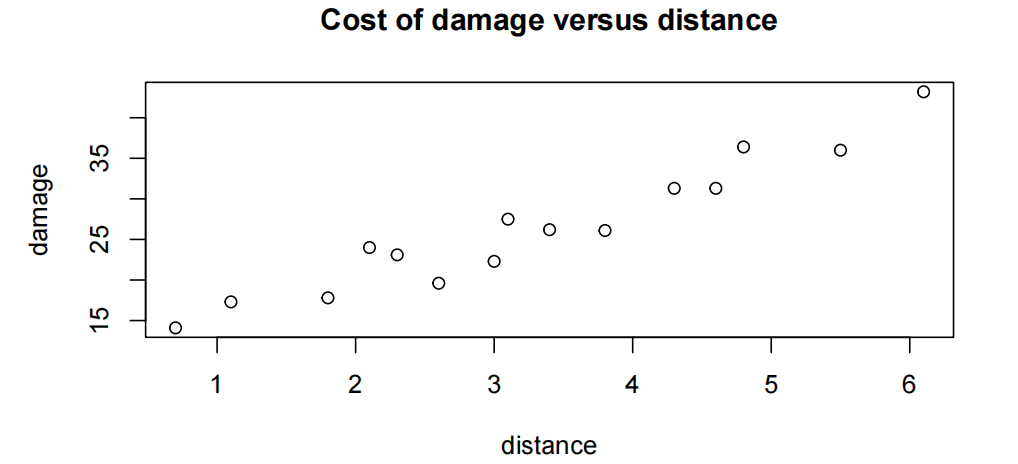
Comment on the plot

毫不奇怪，随着距离消防站的距离和房屋火灾损失的增加，有一个上升的趋势（an increasing trend）。趋势看起来相当线性，围绕这一趋势的可变性看起来相当稳定。

Fit model and check assumptions

fire.fit<-lm(damage~distance,data=fire.df)

plot(fire.fit,which=1)

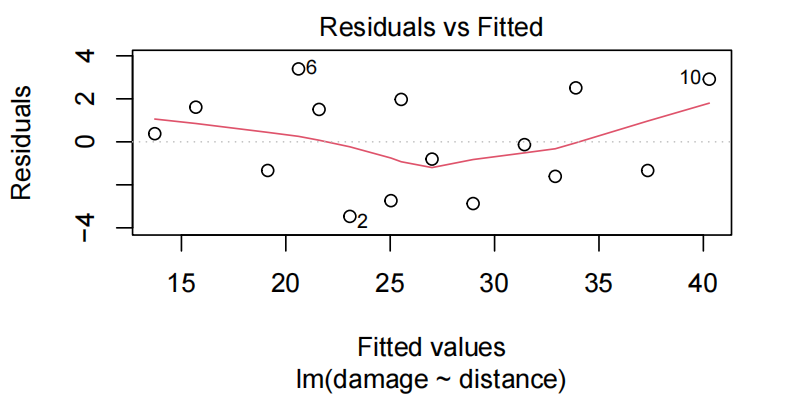
normcheck(fire.fit)

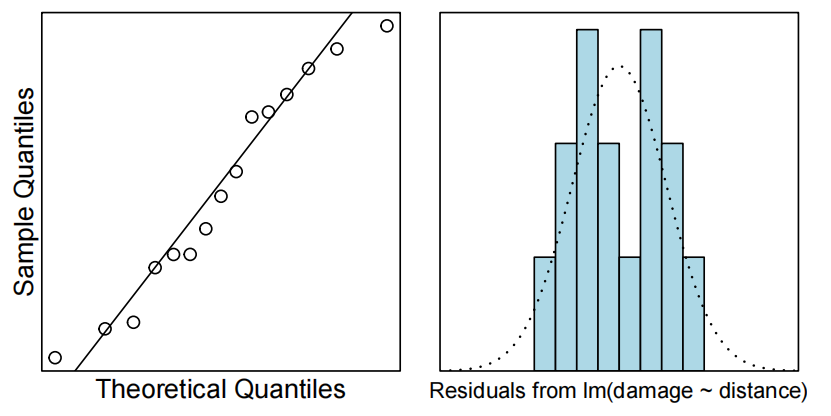
cooks20x(fire.fit)

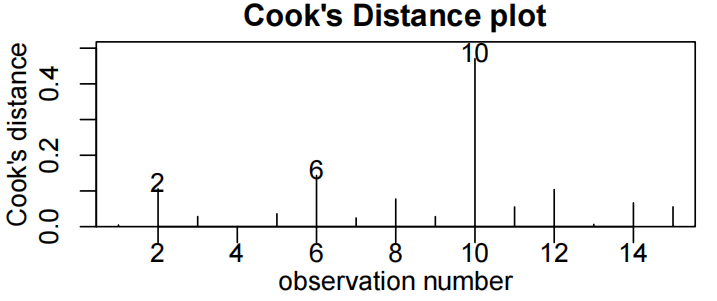
观察到值10超过了库克的距离阈值（threshold）0.4。然而，从拟合的图和残差图（fitted vs residuals plot）中我们可以看到，这一点并不异常（异常的anomalous）——它很有影响力，因为它是离消防站更远的房子（即，解释变量有一个“极端”值）。此外，只有15个观察结果，所以一个点的影响也就不足为奇了。没有理由删除这一点。

summary(fire.fit)

confint(fire.fit)

Plot with superimposed line

plot(damage~distance,main="Cost of damage versus distance",data=fire.df)

adline(fire.fit)

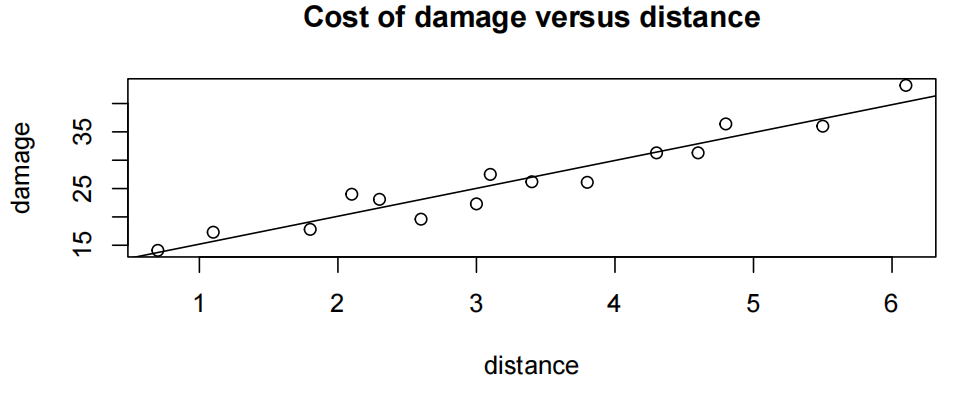
Get additional predicted output

preddistance.df=data.frame(distance=c(1,4))

predict(fire.fit,preddistance.df,interval=“prediction”)

Method and Assumption Checks

损伤与距离的散点图显示了近似恒定散

点的线性关联，因此拟合了一个简单的线性回归模型。我们有一个随机的火灾样本，所以结果应该是相互独立的。在残留图中观察到一个轻微的趋势，但似乎不是主要的问题。观测10的库克距离约为0.5，但并不是一个反常点。我们得出的结论是，所有的假设都是相当令人满意的。我们最终的模型是 $d a m a g e_{i} = β_{0} + β_{1} \times d i s t a n c e_{i} + ε_{i}$ where $ε_{i}$ ~ $i i d N (0, σ^{2})$

我们的模型解释了房屋火灾损失成本的92%。

Executive Summary

一家保险公司希望从距离消防站的距离作为解释变量，来预测房屋着火时发生的损失成本。

毫不奇怪，有强有力的证据表明，房子离消防站越远，它遭受的火灾破坏就越大。我们估计，每离消防站再增加一英里，预期的火灾损失成本就会增加4100美元至5800美元。

我们的模型解释了92%的房屋火灾损害的变化，因此应该是一个合理的预测模型。我们预测，如果在距离消防站1英里的房子里发生新的火灾，损失将在9700美元到20700美元之间。对于距离消防站4英里的房子，我们预计损失将在24,800美元到35,200美元之间。

注：

如果有人担心残差图中的轻微曲率，那么这可以通过在距离上增加一个二次项来检验。这个二次项不显著，因此首选上述简单的线性模型。

虽然这不是一个有趣的问题，但截距对应的是隔壁房屋的损失成本（即零距离）的消防站。在这种情况下，我们估计预计火灾损失为7200美元至13300美元。

Case Study 2.3: Diamond Rings

Problem

该数据集包含来自新加坡零售商随机样本的女士钻石戒指的价格及其钻石石的克拉数。这些戒指由20克拉1金制成，每枚镶嵌一颗钻石。数据是由一位讲师几年前在新加坡收集的，当时他们对建立一个模型来解释钻石戒指的价格很感兴趣。

特别是，希望利用该模型预测两枚戒指的价格：一枚0.3克拉的钻石戒指和一枚1.2克拉的钻石戒指。

测量的变量为：价格：戒指价格（新加坡元）重量：钻石重量（克拉）

Question of interest/goal of the study

我们很想建立一个模型来解释钻石戒指的价格。特别是，我们想预测一枚0.3克拉的钻石戒指和一枚1.2克拉的钻石戒指的价格。

Read in and inspect the data:

diamonds.df=read.table("diamonds.txt", header=T)

head(diamonds.df)

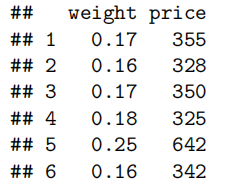
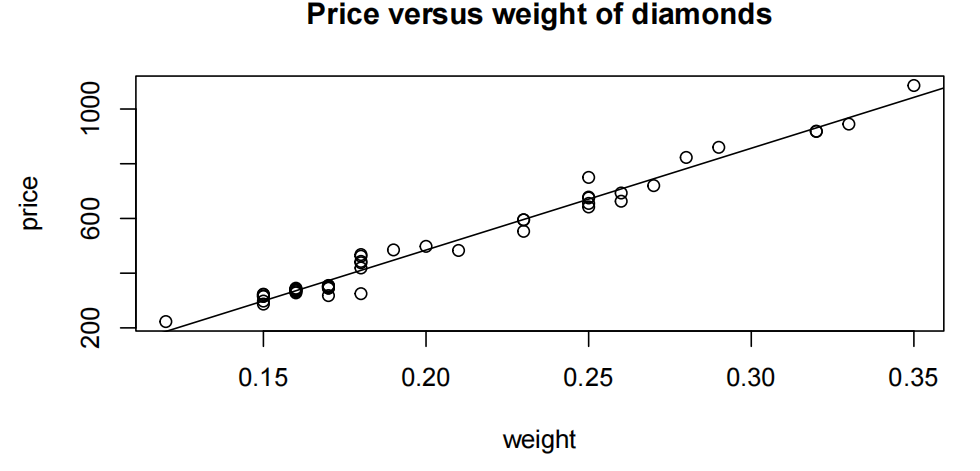
plot(price~weight,main="Price versus weight of diamonds"

,data=diamonds.df)

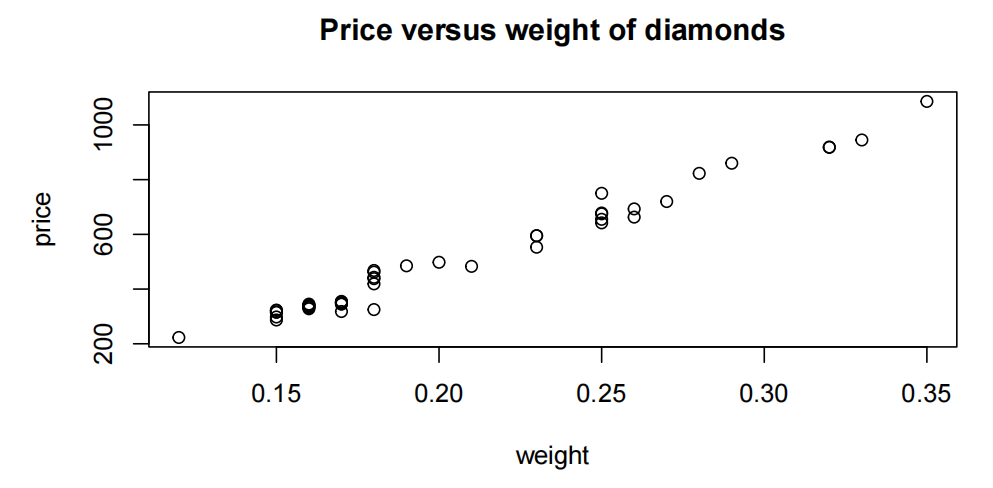
Comment on the plot

价格与权重的散点图（scatter plot）显示了一个很强的、增长的、线性的关系。钻石的重量越大，钻石戒指的平均价格就越大。

Fit model and check assumptions

diamond.fit<-lm(price~weight,data=diamonds.df)

plot(diamond.fit,which=1)

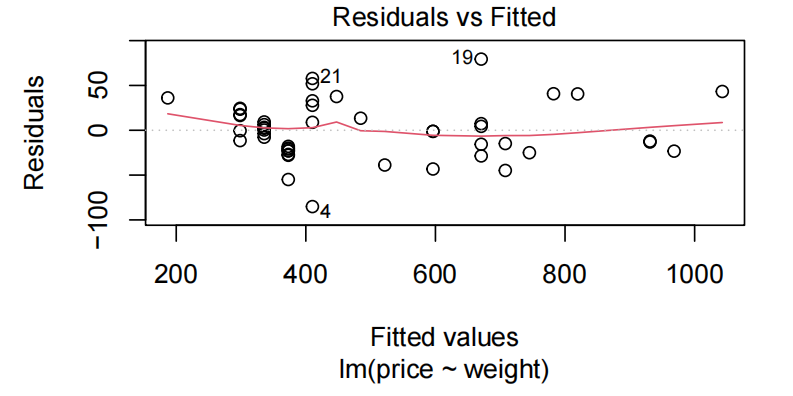
normcheck(diamond.fit)

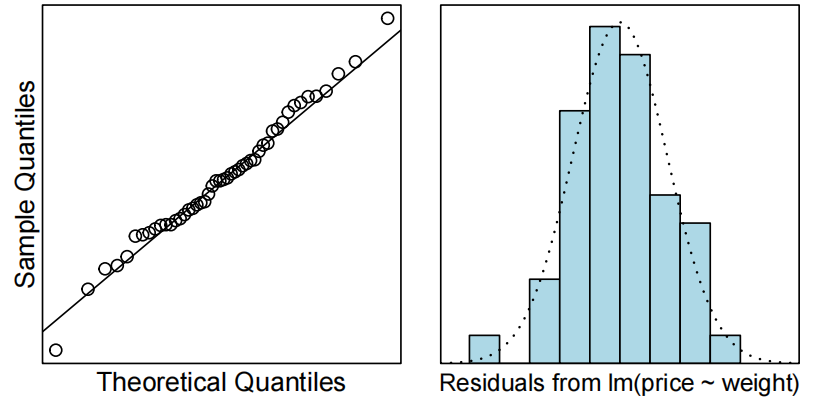
cooks20x(diamond.fit)

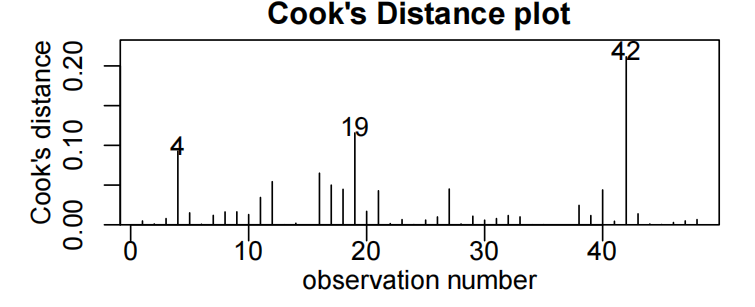
summary(diamond.fit)

#Get summary output and confidence intervals

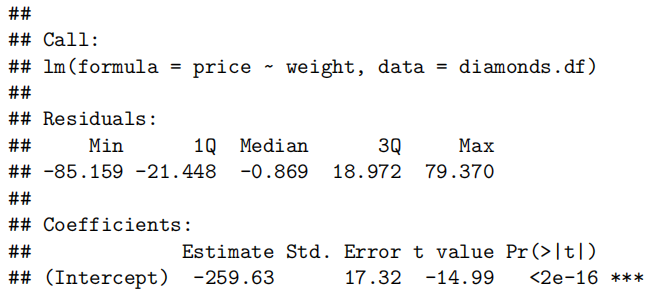
confint(diamond.fit)

Plot with superimposed line

plot(price~weight,main="Price versus weight of diamonds"

,data=diamonds.df)

abline(diamond.fit$coef[1],diamond.fit$coef[2])

Get additional predicted output required

predweight.df=data.frame(weight=c(0.3,1.2))

predict(diamond.fit,predweight.df,interval="prediction")

Method and Assumption Checks

价格与金刚石重量的散点图显示了近似恒定散点的线性关联，因此拟合了一个简单的线性回归模型。

所有的假设都满足了，所以我们在分析中没有问题。我们最终的模型是：

$p r i c e_{i} = β_{0} + β_{1} \times w e i g h t_{i} + ε_{i}, w h e r e ε_{i}$ ~ $i i d N (0, σ^{2})$

我们的模型解释了钻石戒指价格的98%的变化。

Executive Summary

我们从新加坡的零售商那里得到了关于钻石戒指的价格和钻石重量的数据。我们的目标是用钻石戒指的重量来预测钻石戒指的价格。

钻石的重量与戒指价格之间存在强烈的正相关关系——钻石越大，钻石戒指的价格越高。我们估计，每增加0.1克拉的钻石重量，平均钻石戒指的价格会增加360到390美元。

我们的模型解释了98%的钻石戒指价格变化，因此对于预测钻石戒指的价格非常有效。

利用我们的模型，我们预测0.3克拉的钻石戒指价格将在790到920美元之间。

我们的数据仅包括重量不超过0.35克拉的钻石戒指，因此无法依赖1.2克拉戒指的预测。

注：原始数据范围约为900美元，已减少到约130美元，这大约是原始数据的15%，对预测更为有用。

Chapter 3: Equivalence of the null linear model and the one-sample t-test(零线性模型的等价性和单样本t检验)

在本章中，您将学习：

•拟合零模型和进行单样本t检验的等价性。

•配对t检验。

•相关的R代码。

3.1 Revisiting(重新审视) the null model

在线性模型中，默认情况下会拟合截距参数（ $β_{0}$ ）。lm（y~x）不仅拟合了x的效应，还拟合了一个截距。
lm(y~x)是lm(y~1+x)的简化形式。后者明确表示所拟合的模型为
$y = 1 \times β_{0} + x \times β_{1} + ε$ ，其中

ε是iid（其中 $i i d$ 代表Independent and Identically Distributed 的缩写，中文译为 “独立同分布”）的 $N (0, σ^{2})$ 。

这就是为什么可以使用lm(y~1)来拟合零模型或仅包含截距的模型，因为这指定 $y = 1 \times β_{0} + ε$

由于零模型只是简单地指定了y的均值（即期望值），通常会将 $β_{0}$ 标记为µ，此时我们有 $y = μ + ε$ 。这可以用模型公式 $y \sim i i d N (μ ， σ ²)$ 来简化表示。

3.2 Revisiting the t-test

$T = \frac{\overset{―}{y} - μ}{\frac{s}{\sqrt{n}}} \sim t_{n - 1}$ ，其中 $\overset{―}{y}$ 和 $s$ 是我们从样本中计算出的样本均值和样本标准差。

在 10x 课程中，你学习了如何根据包含n个观测值的样本（样本均值为 $\bar{y}$ ，样本标准差为 $s$ ）来计算总体均值 $μ$ 的 95% 置信区间：

$\bar{y}\pm t_{n - 1}^{(0.975)}\frac{s}{\sqrt{n } } $，其中$ t_{n - 1}^{(0.975)}$ 是t 分布乘数。对于95%置信区间，当n>30时，该乘数非常接近2。

R有一个方便的函数来为我们做t检验的计算。为了测试 $H_{0} : μ = 60$ ，我们在t-检验的调用中包括了 $μ = 60$ ：t.test(y,mu=60)

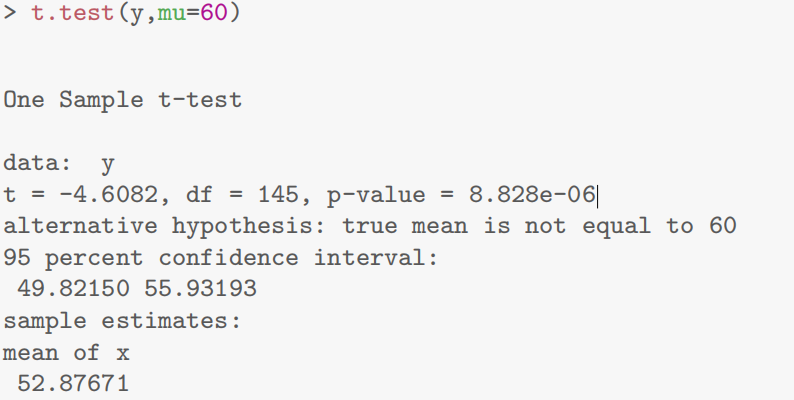
第三章R语言代码总结

1.拟合无解释变量（自变量）的模型（即无x）：

exam.fit=lm(Exam~1, data=Stats20x.df)

confint(exam.fit)

exam.fit60=lm(I(Exam-60)~1, data=Stats20x.df)

coef(summary(exam.fit60))

2.通过t检验可以得到等效输出：（也就是说直接做t检验就好和上面效果是一样的）

t.test(Stats20x.df$Exam,mu=60)

3.对于成对的比较，我们需要创建差异变量：

Stats20x.df$Diff = Stats20x.df$Test2 - Stats20x.df$Exam

4.这两种都可以：

#拟合值的置信区间：

diff.fit=lm(Diff~1, data = Stats20x.df)

coef(summary(diff.fit))

[!success]

在 R 语言中，coef() 函数主要用于提取模型估计的系数。许多建模函数（如线性回归 lm() 、广义线性模型 glm() 等）拟合模型后，返回的对象包含丰富信息，coef() 函数可从中提取模型系数相关信息，方便用户快速获取关键参数估计值。

confint(diff.fit)

或等价于：

t.test(Stats20x.df$Diff)

Case Study 3.1: Exam by itself

Problem

我们希望调查一下考试成绩的分布情况。特别是，我们想要测试这样一个假设，即考试分数的潜在平均值是55分的“历史平均值”。

我们感兴趣的变量是：考试：考试成绩，满分100分。

Question of Interest

我们对建立一个模型来描述考试成绩很感兴趣。特别是，我们想要测试这样一个假设，即考试分数的潜在平均值是55分的“历史平均值”。

Read in and Inspect Data

Stats20x.df=read.table("STATS20x.txt",header=T)

hist(Stats20x.df$Exam,xlab="Exam",main="")

summaryStats(Stats20x.df$Exam)

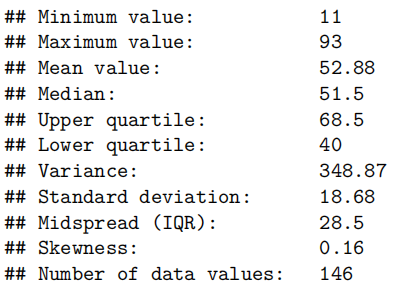
考试成绩刚好集中在50分以上。数据看起来相当单峰和对称——大致正常。有点轻微的右偏斜，但看起来不是问题。

Fitting the null model

mn_exam = mean(Stats20x.df$Exam) # Sample mean

## [1] 52.87671

sd_exam=sd(Stats20x.df$Exam) # Sample standard deviation

## [1] 18.67799

n_exam=length(Stats20x.df$Exam) # Sample size

## [1] 146

tmult_exam=qt(1-0.05/2,df=n_mean-1) # t-multiplier

## [1] 1.97646

CT_exam=mn_exam+tmult_exam*c(-1,1)*sd_exam/sqrt(n_exam) # Confidence Interval

## [1] 49.82150 55.93193

se_exam=sd_exam/sqrt(n_exam) #Standard error

## [1] 1.545802

t_stat_exam=(mn_exam-55)/(se_exam) #t-stat

## [1] -1.373583

pval_exam = 2 * (1 - pt(abs(t_stat_exam), df = n_exam - 1) # p-value*

## [1] 0.171691

examNull.fit55 = lm(I(Exam-55) ~ 1, data = Stats20x.df)

( pval_exam = coef(summary(examNull.fit55))[4] )

## [1] 0.171691

55+confint(examNull.fit55)

## 2.5 % 97.5 %

## (Intercept) 49.8215 55.93193

Finally, with the t.test function

t.test(Stats20x.df$Exam, mu = 55)

##

``## One Sample t-test`

##

``## data: Stats20x.df$Exam`

``## t = -1.3736, df = 145, p-value = 0.1717`

``## alternative hypothesis: true mean is not equal to 55`

## 95 percent confidence interval:

``## 49.82150 55.93193`

``## sample estimates:`

``## mean of x`

``## 52.87671`

Method and Assumption Checks

没有解释变量，因此拟合了一个零模型。

从直方图来看，数据大致呈正态分布，因此满足模型假设。我们的最终模型是

$E x a m_{i} = β_{0} + ε_{i} (o r E x a m_{i} = μ + ε_{i})$ ，where $ε_{i}$ ~ $i i d N (0, σ^{2})$

Executive Summary

我们对构建一个模型来描述考试成绩很感兴趣。

我们估计预期的考试成绩在49.8到55.9分之间（满分100分）。

我们没有理由相信预期的考试成绩与历史平均值55分（满分100分）存在差异（P值= 0.17)。

Chapter 4: Fitting curves(曲线) with the linear model

现在想研究Exam和Assignment的关系

> *## Load the s20x library into our R session*

> library(s20x)

> ## Importing data into R

> Stats20x.df = read.table("Data/STATS20x.txt", header=T)

> ## Examine the data

> plot(Exam ~ Assign, data = Stats20x.df,xlab="Assignment")

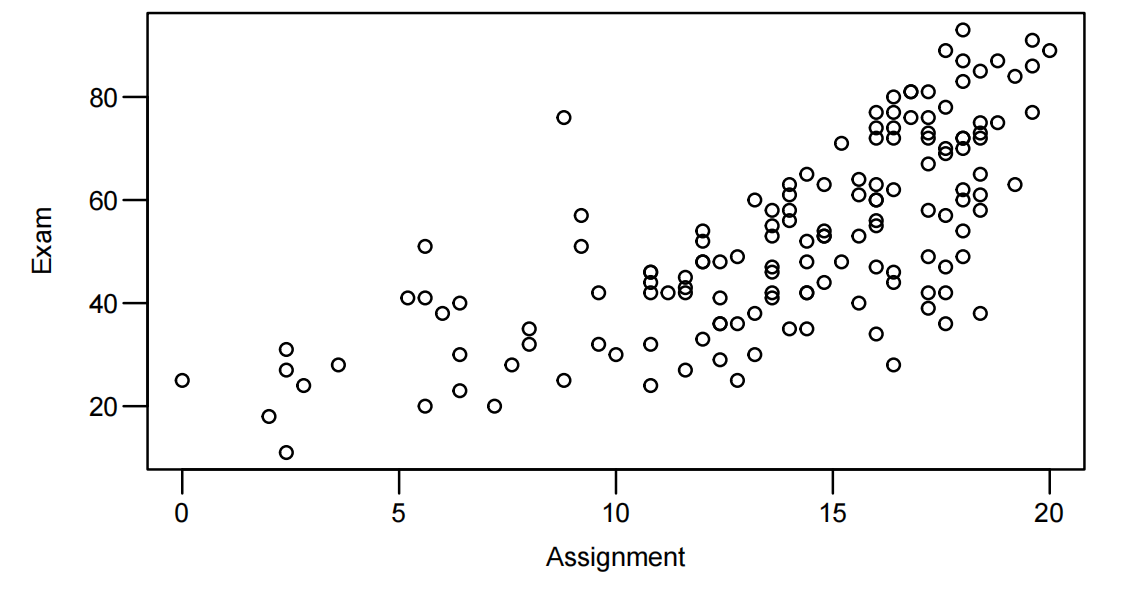
xlab = "Assignment" 属于 plot() 函数的一个参数，xlab 代表 “x - axis label”，也就是 x 轴标签。将其设置成 "Assignment" 后，绘制出的散点图的 x 轴标签就会显示为 “Assignment”。这一操作能让图表的阅读者更清晰地了解 x 轴所代表的变量含义。

带趋势线的散点图:

trendscatter(Exam ~ Assign, data = Stats20x.df,xlab="Assignment")

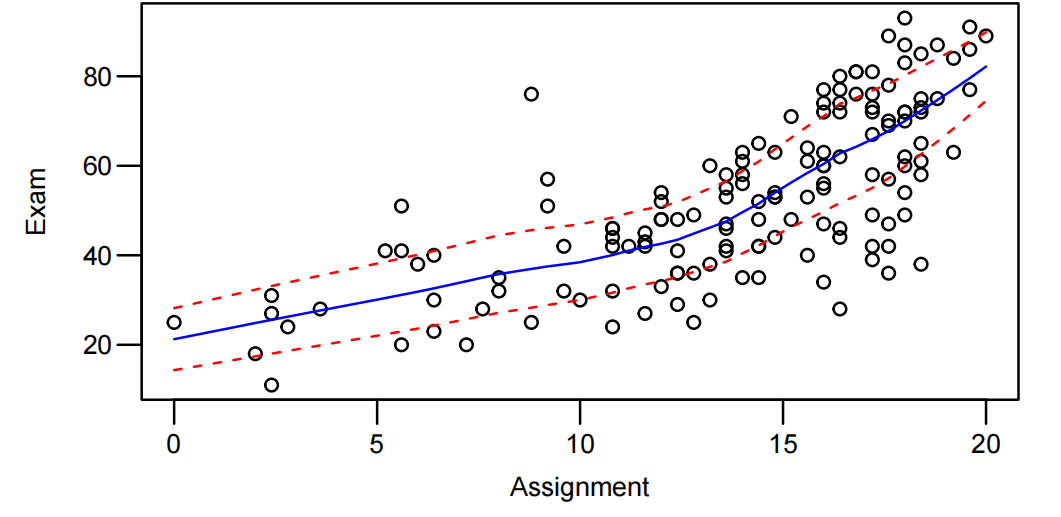
让我们用一个简单的线性模型来拟合这些数据，看看它是否有效。毫不奇怪，我们仍然有一种弯曲的关系。

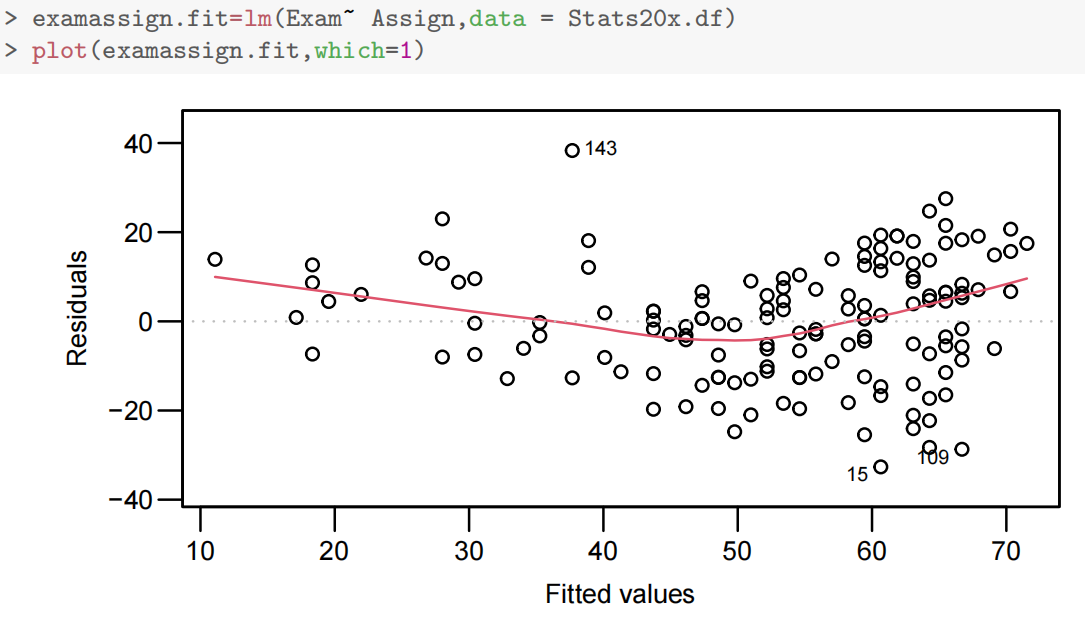
这里假设分布相同且期望值为0的假设似乎值得商榷。中间的负残差较多，但拟合值的极端处的正残差较多。潜在解决方案——为Assign添加二次项（平方项）

因此尝试Section 4.2 Fitting a quadratic（二次） model

课程中 “线性模型” 的定义并非针对变量（如 $x$ ）的形式，而是针对模型中系数$\beta $的线性。具体来说，若模型对任意$ \beta $系数求导结果为常数（不依赖$ \beta$本身），则满足线性模型的要求。

添加一个关于通过 $I$ 进行分配的平方项（ $I (A s s i g n^{2})$ ），如下所示：

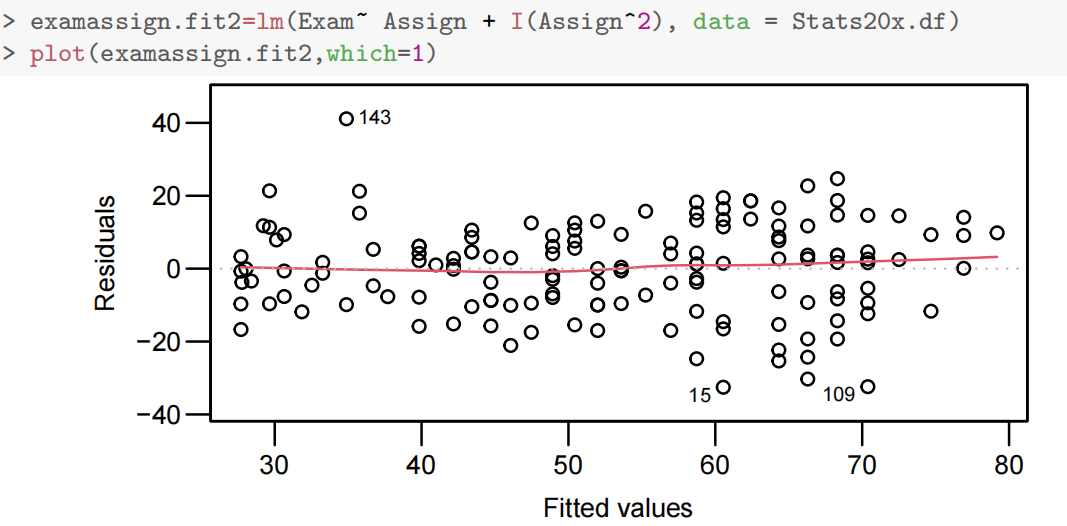
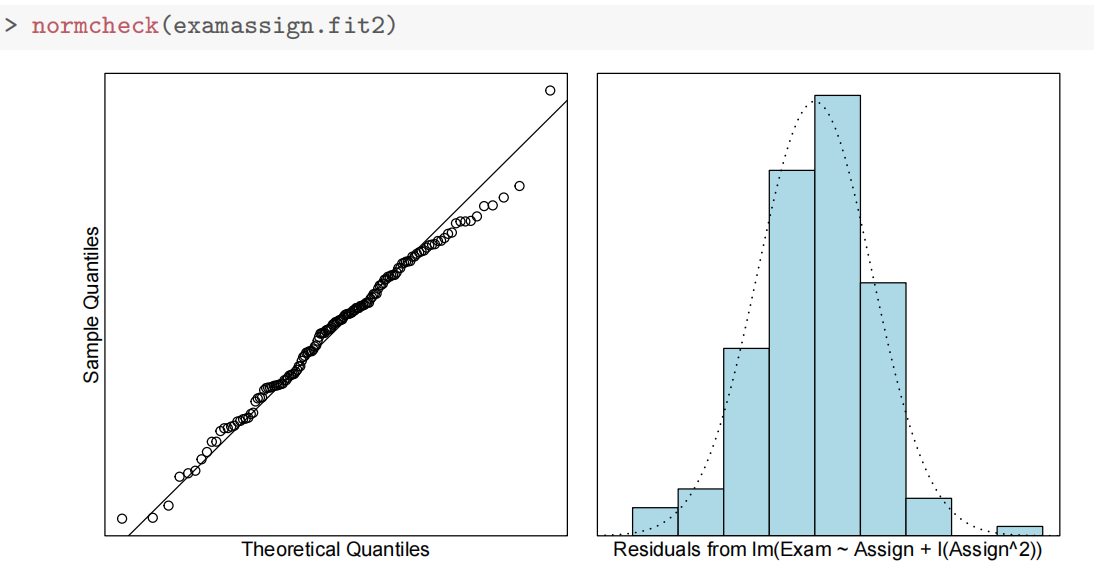
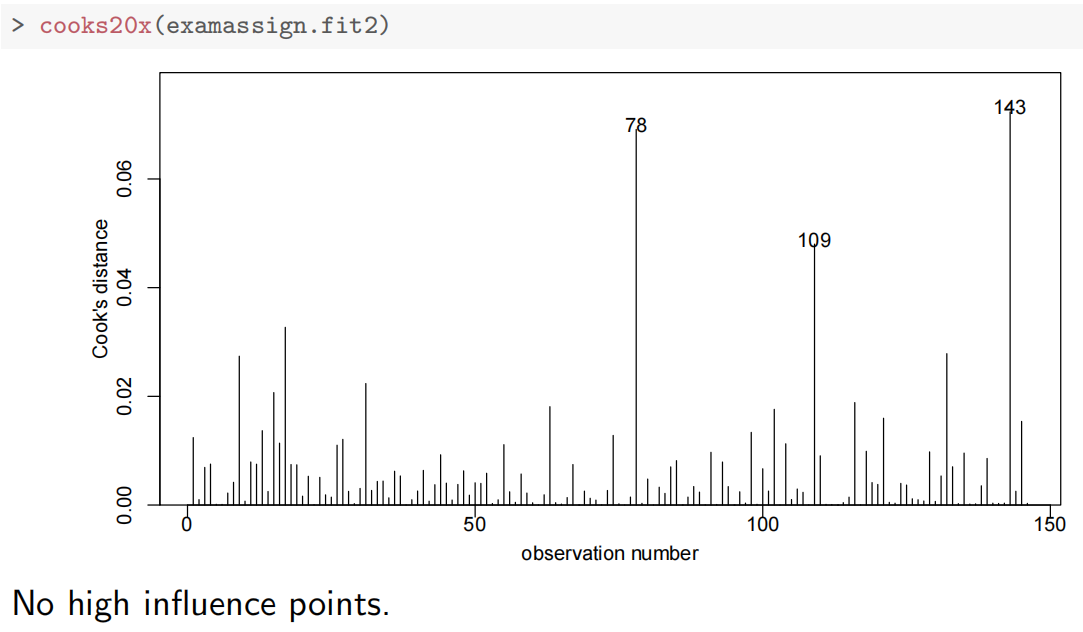
第四章R语言代码总结

二次方程拟合

examassign.fit2-lm(Exam~Assign+I(Assign^2),data=Stats20x.df)

plot(examassign.fit2,which-1)

注：如果零假设 $H_{0}$ ： $β_{2}$ = 0未被拒绝（即 $P - v a l u e > 0.05$ ），那么我们首选的模型将是简单线性回归模型。

Case Study 4.1: Exam vs Assignment mark

Problem

我们希望量化考试成绩和作业分数之间的关系。特别是，当作业分数分别为0、10和20时，我们想要估计所有学生的典型考试分数。

我们感兴趣的变量是：

考试：考试成绩，满分100分。
作业：作业分数为为20分。

Question of Interest

我们想建立一个模型来估计考试分数的考试分数。特别是，当作业分数分别为0、10和20时，我们想要估计所有学生的典型考试分数。

Read in and Inspect the Data

Stats20x.df=read.table("STATS20x.txt,header=T")

plot(Exam~Assign,data=Stats20x.df)

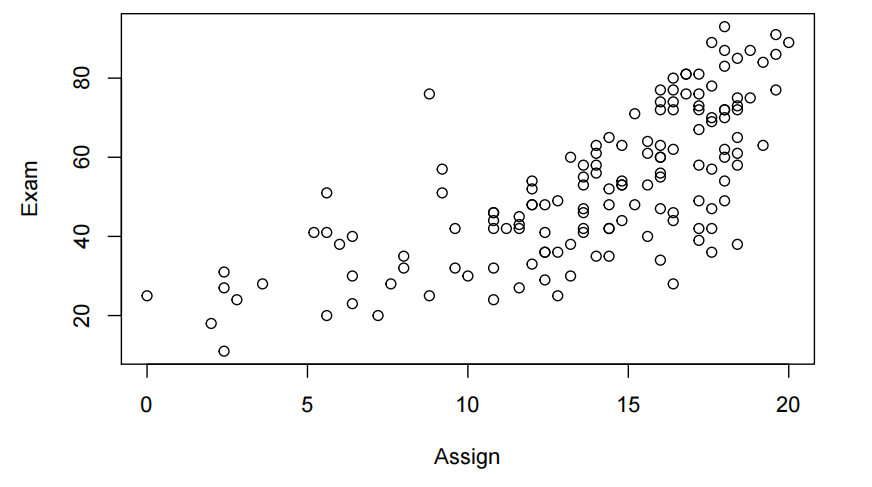
我们看到作业分数和考试成绩之间的关系越来越密切。然而，这种关系似乎不是很强，而且在这种关系中有一些曲率的暗示。我们需要拟合一个线性模型，并仔细检查残差图来验证曲率的范围。

examAssign.fit=lm(Exam~Assign,data=Stats20x.df)

plot(examAssign.fit,which=1)

# We can use this code as an alternative to eovcheck

`plot(examAssign.fit,which=1) 也可以做独立同分布的检验EOVcheck

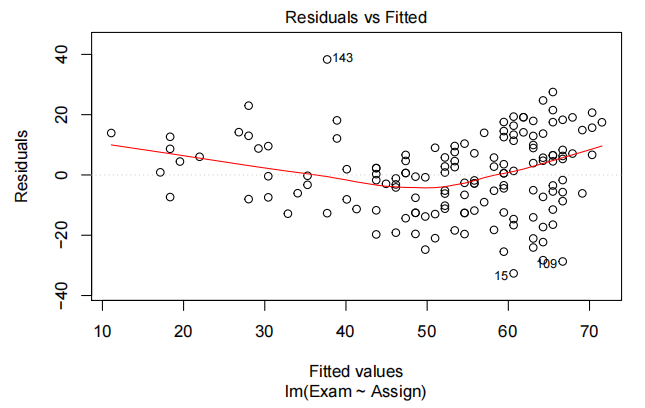
examAssign.fit2=lm(Exam~Assign+I(Assign^2),data=Stats20x.df)

plot(examAssign.fit2,which=1)

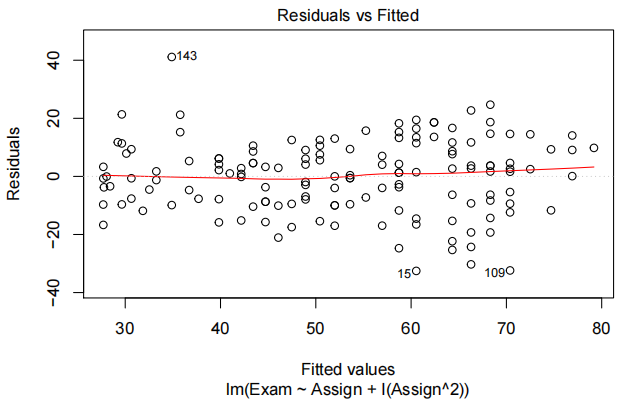
normcheck(examAssign.fit2)

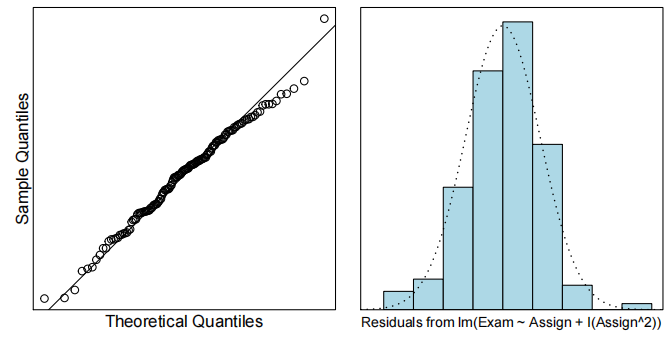
cooks20x(examAssign.fit2)

summary(examAssign.fit2)

##

## Call:

## lm(formula = Exam ~ Assign + I(Assign^2), data = Stats20x.df)

##

## Residuals:

## Min 1Q Median 3Q Max

## -32.541 -9.149 1.273 9.087 41.116

##

## Coefficients:

## Estimate Std. Error t value Pr(>|t|)

## (Intercept) 28.41396 5.99081 4.743 5.05e-06 ***

## Assign -0.68172 1.07242 -0.636 0.525999

## I(Assign^2) 0.16102 0.04545 3.542 0.000536 ***

## ---

## Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

##

## Residual standard error: 12.65 on 143 degrees of freedom

## Multiple R-squared: 0.5477, Adjusted R-squared: 0.5414

## F-statistic: 86.59 on 2 and 143 DF, p-value: < 2.2e-16

confint(examAssign.fit2)

Get additional Prediction Intervals

注意，由于我们是在典型的考试分数之后，所以我们使用了置信区间而不是预测区间。

predAssign.df=data.frame(Assign=c(0,10,20))

predict(examAssign.fit2,predAssign.df,interval='confidence')

Method and Assumption Checks

考试标记与分配标记的散点图显示了该关系中的曲率。我们从一个线性模型开始，用作业分数来描述考试分数。从一个简单的线性模型拟合的残差图显示出相当稳定的散射，但有很强的曲率。因此，在线性模型中添加了一个二次项。一旦我们将二次项加入到线性模型中，所有的模型假设看起来都很满足。我们最终的模型是： $E x a m_{i} = β_{0} + β_{1} \times A s s i g n_{i} + β_{2} \times A s s i g n^{2} + ε_{i}$

where $ε_{i}$ ~ $i i d N (0, σ^{2})$

我们的模型解释了学生期末考试成绩变化的55%。

Executive Summary

我们对构建一个模型来估计考试成绩与作业成绩之间的关系很感兴趣。

期望的考试分数与作业分数之间的关系为二次关系。

在这里，如果作业分数增加一个分数，预期考试分数的增加会随着作业分数的增加而增加。例如，对于作业达到7或8分的人，预期考试成绩没有什么差别，但对于17或18分的人，差别要大得多。

作业分数为0、10、20时，估计预期考试分数分别在16.6~40.3， 34.3~41.1和 73.6~84.8之间。

Chapter 5: Linear models with a 2-level categorical (factor) explanatory variable（具有2级分类（因素）解释变量的线性模型）

1.第五章聚焦于如何在线性模型中使用两水平分类（因子）解释变量，以学生考试成绩（Exam）与出勤情况（Attend，分 "Yes" 和 "No"）为例，主要内容为：

数据预处理（确保Attend为因子变量）

\# 加载数据（假设数据已导入为Stats20x.df）

# Stats20x.df = read.table("Data/STATS20x.txt", header = T)

# 将Attend转换为因子变量（确保R识别为分类变量）

Stats20x.df$Attend = as.factor(Stats20x.df$Attend)

# 检查因子水平（基线为"No"，对比组为"Yes"）

levels(Stats20x.df$Attend) # 输出: [1] "No" "Yes"（字母顺序决定基线）

拟合线性模型（自动生成指示变量）查看模型结果（获取 β0、β1 及显著性）

# 用因子变量Attend拟合模型，lm自动以"No"为基线（β0），"Yes"为对比组（β1）

examattend.fit = lm(Exam ~ Attend, data = Stats20x.df)

# 模型摘要（直接显示系数估计值、t值、p值）

summary(examattend.fit)

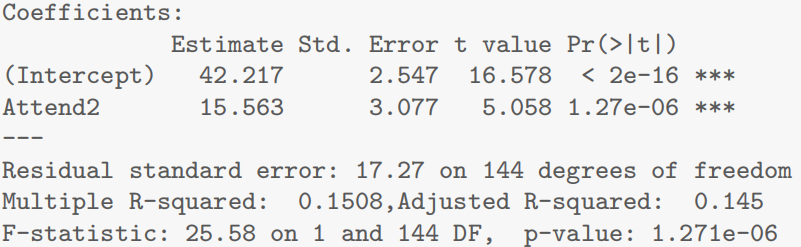
β0（基线组 No 的平均成绩）：(Intercept) 的估计值 42.2174

β1（对比组 Yes 与基线组的均值差异）：AttendYes 的估计值 15.5626

t 值：AttendYes 对应的 t value 为 5.058（检验 β1 是否为 0）

在含两水平分类变量的线性模型中， $β_{1}$ 表示对比组与基线组的均值差异（如出勤者与非出勤者的平均成绩差）。t值通过计算 $β_{1}$ 估计值与其标准误的比值，检验 $β_{1} = 0$ （即两组均值无差异的原假设）若t值绝对值大且p值小，则拒绝原假设，表明两组均值存在显著差异。

p 值：Pr(>|t|) 为 1.27e-06（远小于0.05，显著拒绝β1=0）

获取 β1 的置信区间

# 计算95%置信区间（包含β1的可能取值范围）

confint(examattend.fit, parm = "AttendYes") # 单独获取β1的置信区间

# 或直接获取所有系数的置信区间

confint(examattend.fit)

β1 的 95% 置信区间：[9.48, 21.64]，即出勤者平均成绩比非出勤者高 9.48~21.64 分。

等价代码：手动创建指示变量（文中早期演示代码，非必需）

为了演示原理，文中早期手动创建了指示变量 Attend2（0=No，1=Yes），代码如下（与上述lm(Exam ~ Attend)等价）

# 手动创建指示变量（0=No，1=Yes）

Stats20x.df$Attend2 = as.numeric(Stats20x.df$Attend == "Yes")

# 拟合模型（此时解释变量为数值型Attend2，β1为均值差异）

examattend2.fit = lm(Exam ~ Attend2, data = Stats20x.df)

summary(examattend2.fit)

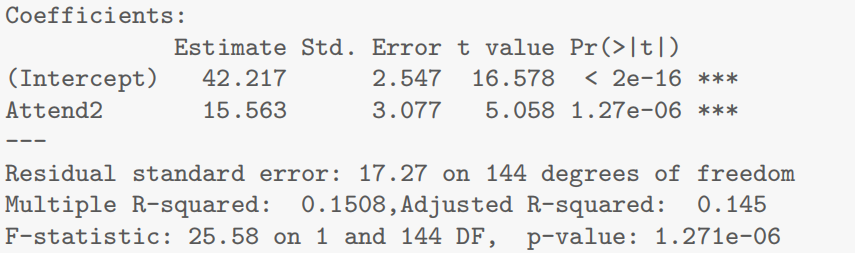
可见 Attend2 的系数（15.563）、t 值、p 值与 AttendYes 完全一致，验证了lm自动处理因子变量的等价性。

核心代码为 lm(Exam ~ Attend, data = Stats20x.df)，通过 summary() 和 confint() 直接获取：

β0：截距项（基线组均值）
β1：对比组系数（均值差异）
显著性：t 值和 p 值（检验 β1 是否为 0）
置信区间：confint() 输出 β1 的区间范围

R 语言通过自动处理因子变量，避免了手动创建指示变量的繁琐，直接通过模型公式实现两水平分类变量的线性回归分析。

也就是说要分析0-1变量对某个变量的影响，正常按照lm创建即可，这时候R语言默认 $β_{0}$ 就是0-1变量为0对应的结果，而 $β_{1}$ 本来是对应斜率，这时候就对应了0-1变量为1对应的结果（相当于1对应结果就等于） $β_{0} + β_{1} \times 1$ ，不必理会书中自行创建指示变量的操作，这是为了说明R语言的便利性

指示变量（Indicator Variables）的应用：

将两水平分类变量（如 Attend）转换为数值型指示变量（0/1），其中基线水平（如 "No"）为 0，对比水平（如 "Yes"）为 1。

lm函数会自动处理因子变量，无需手动创建指示变量，默认以字母顺序的第一个水平为基线（参考组），模型系数表示对比组与基线组的均值差异（如 “出勤效应”）。

线性模型构建与解释：

模型形式为

$E [Exam | Attend] = β_{0} + β_{1} \cdot AttendYes$ ，其中：

$β_{0}$ 是基线组（非出勤者）的平均成绩，

$β_{1}$ 是对比组（出勤者）与基线组的均值差异。

通过回归结果可直接获取两组均值差异的估计值 $\hat{β_{1}}$ 、显著性（t 值和 p 值）及置信区间。

模型假设与检验：

验证线性模型假设（独立、同分布、正态性），通过残差图、正态性检验（如normcheck）和 Cook 距离检查异常值。

结果表明，出勤者平均成绩比非出勤者高约 15.56 分，且差异极显著（p 值 < 0.001）。

两样本 t 检验与线性模型的关联：

当解释变量为两水平因子时，线性模型与两样本 t 检验本质等价，均用于检验两组均值是否存在显著差异。

2.什么是 t 检验，作用、适用场景及如何根据结果得出结论？

t 检验的定义： t 检验是一种统计假设检验方法，用于判断两个组的均值是否存在显著差异，适用于小样本或总体方差未知的情况。根据数据类型分为：

独立样本 t 检验（如本案例，比较两组独立样本的均值，如出勤 vs 非出勤学生）；

配对样本 t 检验（比较同一组样本在不同条件下的均值，如前后测数据）。

作用：

检验两组数据的均值是否来自均值相同的总体（原假设 $H_{0} : μ_{1} = μ_{2}$ ；

量化均值差异的显著性（p 值）和效应大小（均值差、置信区间）。

适用场景：

当研究问题涉及两组独立或配对样本的均值比较，且数据近似正态分布时，使用 t 检验。

例如：验证 “使用新疗法的患者平均康复时间是否短于传统疗法”“男性与女性的平均收入是否有差异”。

如何根据结果得出结论？ 以本案例的两样本 t 检验结果为例（假设检验$H_0: \mu_{\text{Yes } } = \mu_{\text{No } } $：

t 值与 p 值：

t 值为 5.058，绝对值越大，均值差异越显著；

p 值为 1.27e-06（<0.05），拒绝原假设，说明出勤组与非出勤组的平均成绩存在显著差异。

均值差与置信区间：

样本均值差为 15.56 分（出勤组 - 非出勤组），95% 置信区间为 [9.48, 21.64]，说明出勤者平均成绩比非出勤者高 9.48~21.64 分，且该差异不包含 0，进一步支持显著性结论。

实际意义：

结合业务背景解读结果，如 “定期出勤对提高考试成绩有显著正向影响，平均提升约 15.56 分”。

3.为什么无需手动创建指示变量，且最后给出的R code都是正文中没有的代码？

R 的lm函数会自动将因子变量转换为指示变量（0/1），无需用户干预。例如：

因子变量Attend（水平为 "No" 和 "Yes"）会被自动处理为：

基线水平 "No" 对应 0，系数为截距项 $β_{0}$ （非出勤者平均成绩）；

对比水平 "Yes" 对应 1，系数为 $β_{1}$ （出勤者与非出勤者的均值差）。

手动创建指示变量（如Attend2 = as.numeric(Attend=="Yes")）是为了演示原理，实际建模时lm会隐式完成，简化代码并避免错误。

新增代码的目的：最后给出的代码（如lm(Exam~Attend-1)）是对正文内容的拓展和补充，展示lm函数的高级用法：

Attend-1表示移除模型截距项，直接拟合两组的均值作为独立参数（AttendNo 和 AttendYes），适用于需要单独估计各组均值而非对比基线的场景（如无截距模型）。

这类代码在正文中未详细说明，因为正文聚焦基础用法（含截距的基线对比模型），但实际建模中可能需要根据需求调整（如多水平因子分析）。

如果这两组有明显不同的方差，那么一种方法是放弃使用线性模型，使用修正的t检验，而不使用方差相等的假设。修改后的t检验方法将不会用于本课程。（也就是说写这个代码就默认方差是相同的，不用管var.equal，因为默认为true就是我们想要的）

4.为什么最后提到为什么 lm 等价于做 t 检验？

当解释变量是两水平因子时，线性模型与两样本 t 检验（假设方差齐性，var.equal=TRUE）在以下方面完全等价：

假设检验目标一致：

线性模型通过检验系数 $β_{1} = 0$ （即对比组与基线组的均值差为 0），等价于 t 检验的原假设$H_0: \mu_{\text{Yes } } = \mu_{\text{No } } $。

统计量与结果一致：

lm输出的t值和p值与t.test(var.equal=TRUE)完全相同（如案例中均为 t=5.058，p=1.27e-06）；

均值差的置信区间一致（如lm中 $β_{1}$ 的置信区间与 t 检验的 “差异估计值” 置信区间相同）。

模型本质相同：

两样本 t 检验是线性模型的特例，当解释变量为两水平因子时，线性模型退化为检验两组均值差异的 t 检验。二者的数学原理一致，只是输出形式不同（线性模型给出回归系数，t 检验直接给出均值差）。

第五章R语言代码总结

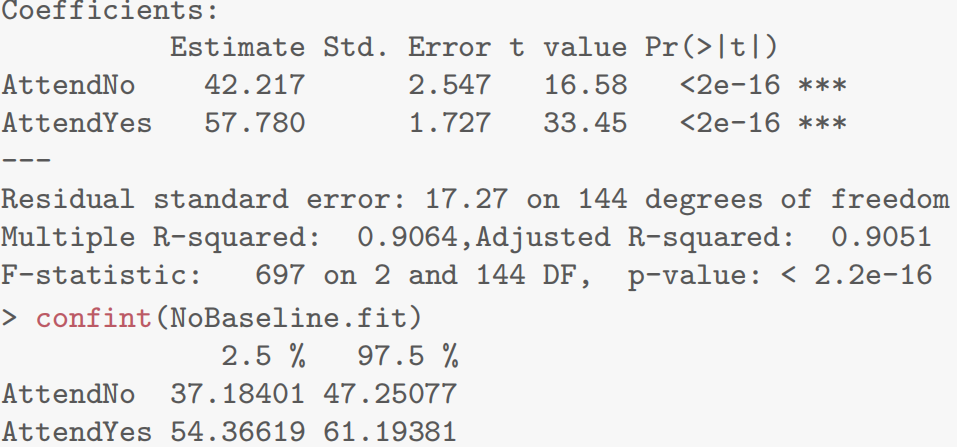
1.R提示和技巧：模型公式中使用-1

在某些情况下，拟合模型时没有基线水平的截距是有用的。这很简单，只需在模型公式中添加-1：

> NoBaseline.fit=lm(Exam~ Attend-1, data = Stats20x.df)

> summary(NoBaseline.fit)

注：当模型中没有截距项时， $R^{2}$ 没有意义。

[!s]

文档中强调的lm(Exam ~ Attend)是99% 场景下的标准用法，R 自动处理基线和指标变量，符合线性模型的核心逻辑（截距 + 组间差异）。

无截距模型属于特殊设定，使用场景极少，且输出解释与常规模型不同（系数代表绝对均值，而非差异），过早学习可能混淆对 “基线水平”“截距” 等基础概念的理解。

2.本章所需的大部分R代码

您不需要创建指标变量，因为R会为您完成这项工作。它将为您选择基线，

> examattend.fit = lm(Exam~ Attend, data = Stats20x.df)

只需关注上面这个正常拟合即可，其他代码都不需要管

这相当于

> t.test(Exam~ Attend, var.equal=TRUE, data = Stats20x.df)

Case Study 5.1: Exam vs Attendance

Problem

我们希望确定定期上课是否与考试成绩有关。特别是，我们想要估计参加者和非参加者的预期考试分数，并预测个体参加者和非参加者的实际考试分数。

关注的变量包括：

考试：考试成绩，满分100分。
出勤：一个两级分类变量，有Yes和No.两个等级。

Question of Interest

我们想要量化考试成绩和出勤率之间的关系。特别是，我们想要估计参加者和未参加者的预期考试成绩，并预测个别参加者和未参加者的实际考试分数。

Read in and Inspect the Data

Stats20x.df=read.table("STATS20x.txt",header=T)

#could of also used plot(Exam~Attend,data=Stats20x.df)

boxplot(Exam~Attend,data=Stats20x.df)

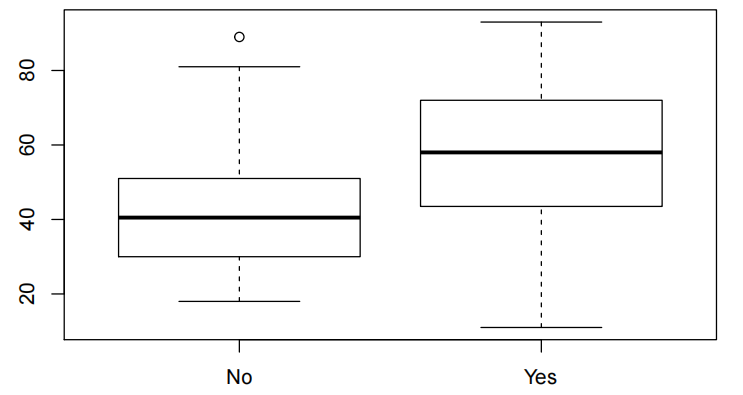
参加考试的学生的分数似乎比不经常上课的学生的分数集中。两组的箱线图看起来相当对称。

Model Building and Check Assumptions

examAttend.fit=lm(Exam~Attend,data=Stats20x.df)

eovcheck(examAttend.fit)

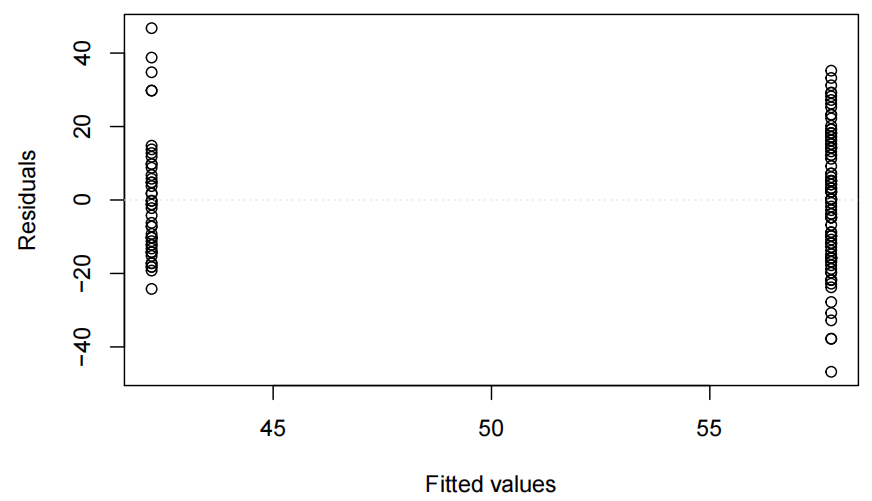
normcheck(examAttend.fit)

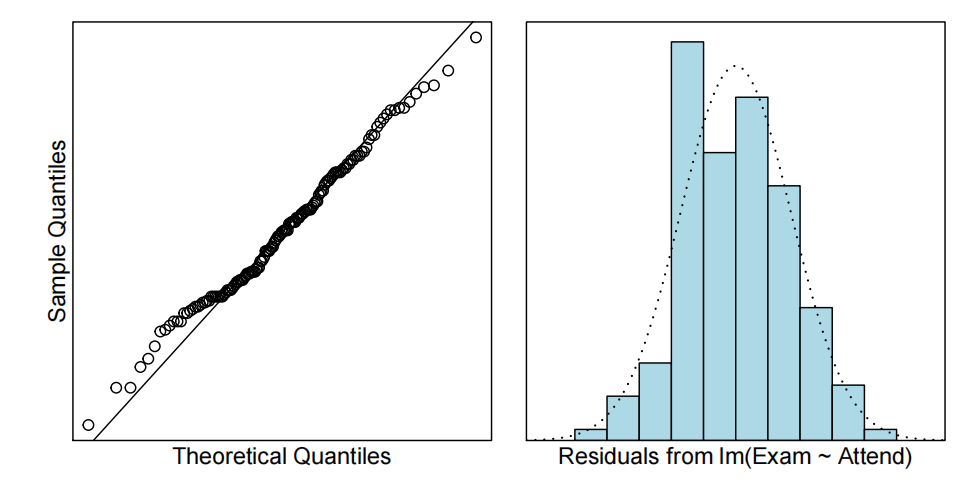
cooks20x(examAttend.fit)

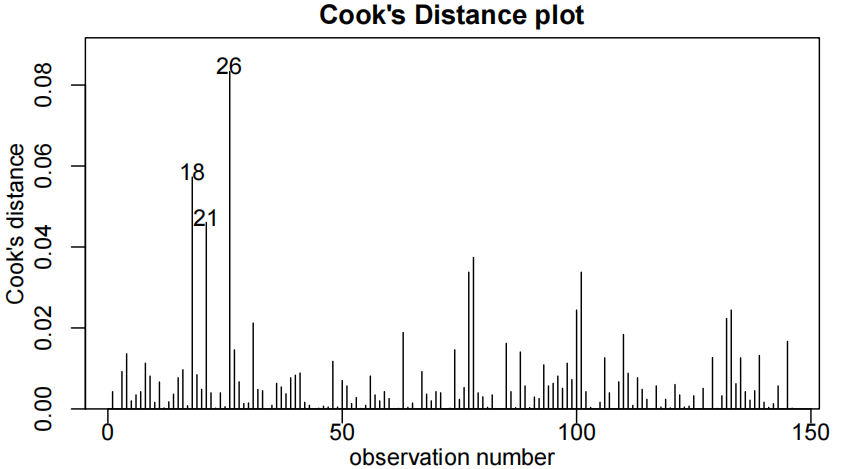
summary(examAttend.fit)

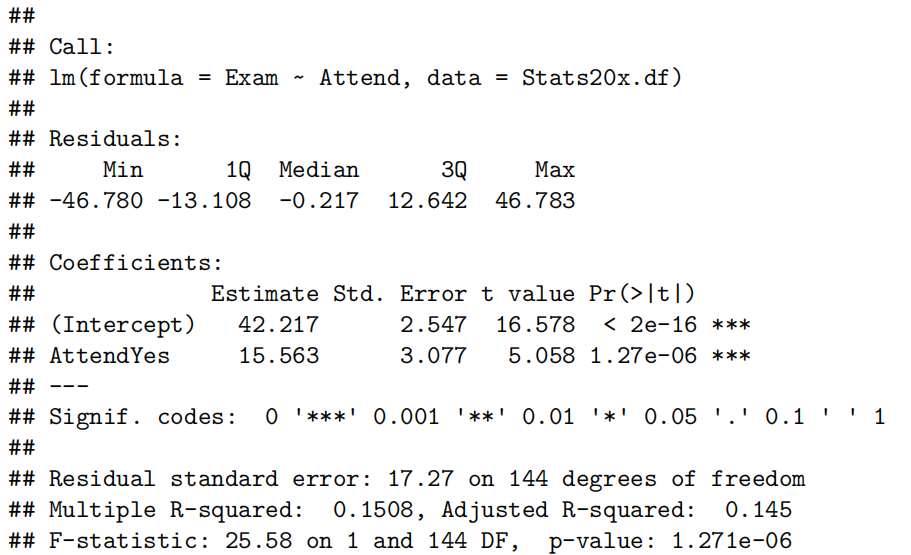
confint(examAttend.fit)

Get additional Prediction Intervals

先用confidence再用prediction：先获取整体预测情况再获取个体预测情况

predAttend.df=data.frame(Attend=c("No","Yes))

# Using interval = "confidence"' to get CI(confidence interval) for expected exam score

*# for each level of Attend*

predict(examAttend.fit,predAttend.df,interval="confidence")

# Using interval = "predition"' to get PI（prediction interval） for individual student's exam score

*# for each level of Attend*

predict(examAttend.fit,predAttend.df,interval="prediction")

Method and Assumption Checks

我们希望用出勤率来解释考试成绩，这是一个两层因素。因此，我们拟合了一个包含单个解释变量的线性模型。（注意，这相当于进行了一次两样本t检验）。

有四位未出勤的学生表现异常出色（即，正向残差较大），但由于样本量较大，这一点影响不大。因此，所有模型假设都得到了满足。

我们的最终模型为： $E x a m_{i} = β_{0} + β_{1} \times A t t e n d . Y e s_{i} + ε_{i}$ ，where

$ε_{i} \sim i i d N (0, σ^{2})$ 。这里， $A t t e n d . Y e s_{i} = 1$ 表示学生经常出勤（即回答“是”），否则为零（即“否”）。我们的模型解释了学生最终考试成绩变异性的15%。

Executive Summary

我们希望量化考试成绩与出勤率之间的关系（quantify the relationship between … and …）。

有强有力的证据表明，出勤的学生比不参加课程的学生考试成绩更高（P值≈10−6）。我们估计，定期出勤可以将学生的预期考试成绩提高（increase）9.5到21.6分（满分100分）。

非出勤者和出勤者的预期考试成绩分别为37.2到47.3分和54.4到61.2分。

单个非出勤者和出勤者的预测考试成绩分别为7.7到76.7分和23.5到92.1分。

我们的模型仅能解释学生最终考试成绩变异性（variability）的15%，这在预测方面表现不佳（and this would not be good for prediction）。我们可以通过观察预测区间的宽度（how wide our prediction intervals）来了解这一点。

Chapter 6: Multiplicative（乘法） linear models（指数模型）

均值与中位数方面，对于房价、收入这类右偏数据，中位数比均值更能代表 “典型” 值，因为均值易受极端值影响。对数变换可让偏态数据接近正态分布，便于利用线性模型推断中位数，在对数尺度下均值与中位数相等，回 transform 后对应原尺度的中位数。

对数变换与乘法模型的作用是将解释变量的乘法效应转化为对数尺度上的加法效应，例如房价随年龄的指数折旧可转化为对数尺度的线性递减。其步骤为对响应变量 $y$ 取对数 $l o g (y)$ ，拟合线性模型，再通过指数变换 $e x p ()$ 回 transform 结果，可解释为中位数的乘法效应。

该模型的应用场景包括数值解释变量，如汽车价格随年龄的折旧（乘法递减）；以及分类解释变量，如不同拖网类型对副渔获物的影响（组间中位数的倍数差异）。R 代码核心有：拟合对数尺度模型用lm(log(y) ~ x, data = df)；回 transform 置信区间用exp(confint(model))；假设检验使用残差图（plot(model, which=1)）和正态性检验（normcheck(model)）。

案例 1：奥克兰房价 - 均值 vs 中位数推断

问题：估计偏态分布的房价数据中，“典型” 房价（均值 vs 中位数）。
数据：94 套奥克兰房屋售价（单位：$1000），右偏分布（均值 > 中位数）。

Houses.df <- read.table("Data/AkldHousePrices.txt", header = T)

hist(Houses.df$price, breaks = 20, xlab = "Price ($1000)")

abline(v = mean(Houses.df$price), col = "blue", lwd = 2)

abline(v = median(Houses.df$price), col = "green", lwd = 2)

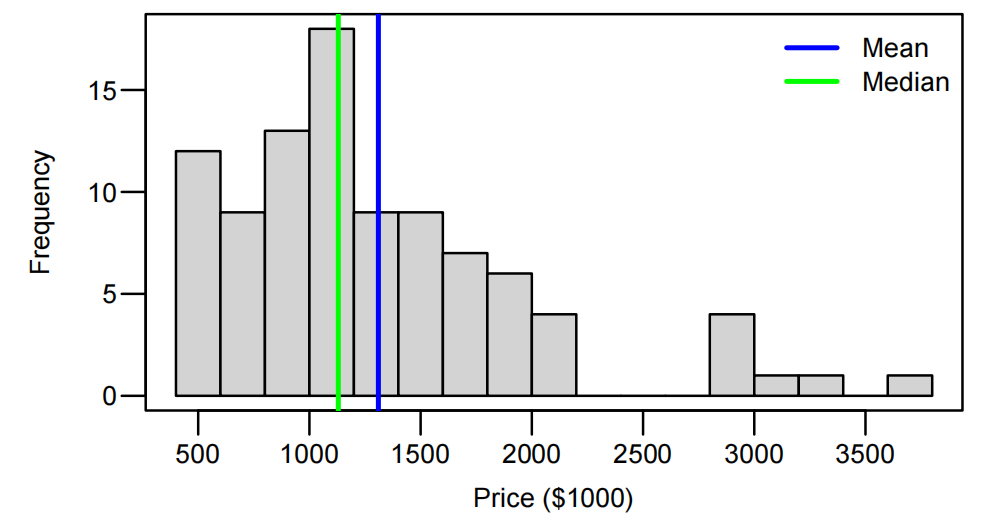
summary 统计显示右偏：均值 1310.1，中位数 1130。

对数变换与模型拟合：

对价格取对数，拟合空模型（截距项）

LoggedPriceNull.fit <- lm(log(price) ~ 1, data = Houses.df)

回 transform 置信区间得到中位数估计：

exp(confint(LoggedPriceNull.fit))

结果：中位数 95% CI 为 [1055.35, 1285.86]（单位：$1000），即$1.06M 至 $1.29M，较均值 CI 更合理（因排除极端值影响）。

结论：

右偏数据中，对数变换后的线性模型适用于推断中位数，结果比均值更稳健。

案例 2：马自达汽车价格与年龄 - 乘法线性回归

问题：分析汽车价格随年龄的折旧模式（加法 vs 乘法效应）。
数据：123 辆马自达汽车的价格（AUD）与制造年份（1991 年数据，年龄 = 1991 - 年份）。

数据准备：

创建年龄变量并绘制散点图，显示价格随年龄指数递减（非恒定散点，提示乘法效应）：

Mazda.df <- read.table("Data/mazda.txt", header = T)

Mazda.df$age <- 91 - Mazda.df$year

plot(price ~ age, data = Mazda.df, xlab = "Age", ylab = "Price (AUD)")

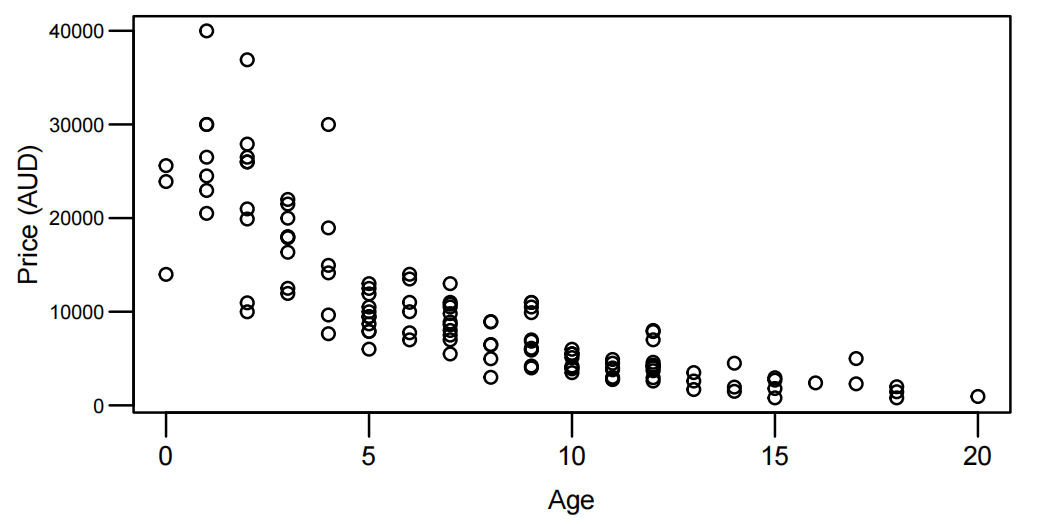
对数变换与模型拟合：

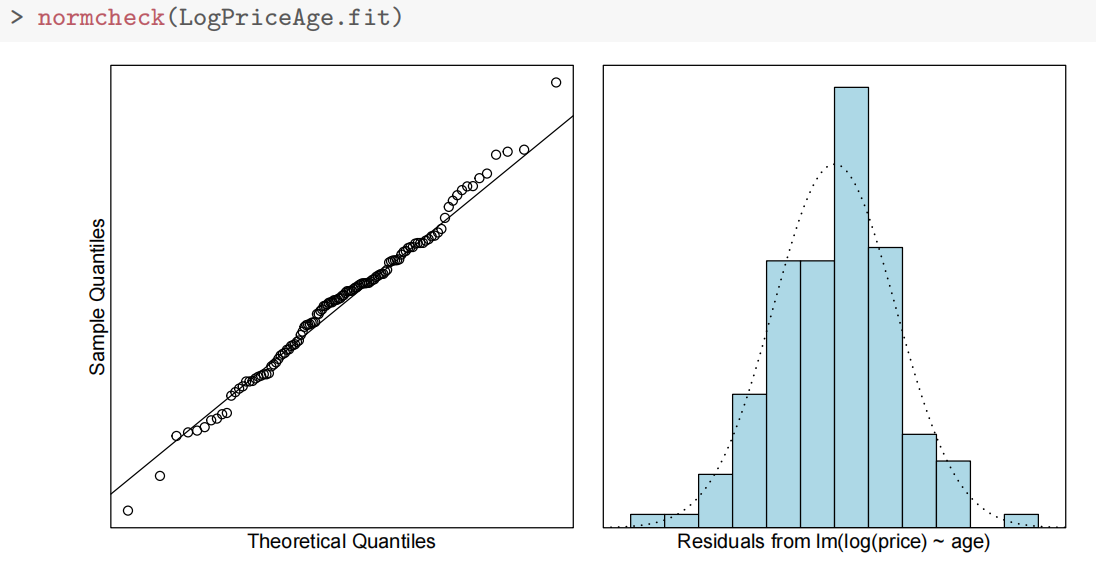
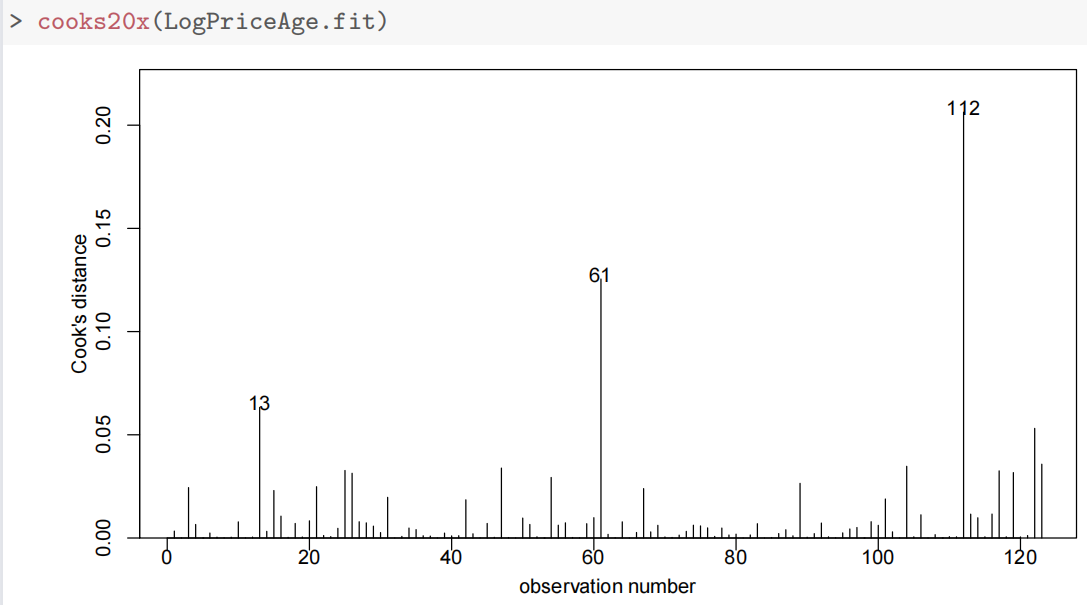
LogPriceAge.fit <- lm(log(price) ~ age, data = Mazda.df)

plot(LogPriceAge.fit,which=1)

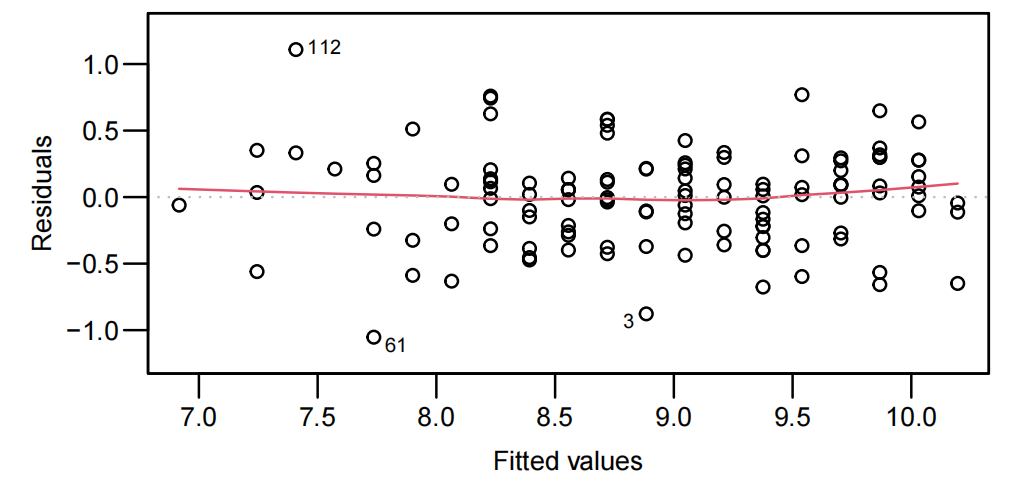
summary(LogPriceAge.fit)

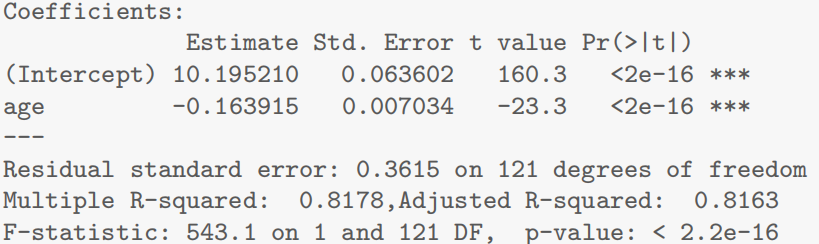
模型输出显示年龄系数显著 ${\hat{β}}_{1} = - 0.1639$ ，表示年龄每增加 1 年，对数价格减少 0.1639，对应原尺度中位数价格乘以 $e^{- 0.1639} \approx 0.85$ （即每年贬值 15%）。

假设检验与结果：

残差图显示等方差假设满足，Cook 距离无异常值。

回 transform 置信区间：

exp(confint(LogPriceAge.fit))

截距项 CI 对应新车中位数价格 [23607, 30367] AUD，年龄系数 CI 对应年贬值率 13.9%~16.3%。

结论：

价格随年龄呈指数衰减，乘法模型（对数变换）能有效捕捉这种递减趋势。

案例 3：拖网类型对副渔获物的影响 - 分类解释变量

问题：比较两种拖网（标准型 vs 锥形）的副渔获物重量，是否存在乘法效应。
数据：50 次捕捞数据，副渔获物重量（kg），拖网类型为二分类变量。

数据探索：

Bycatch.df <- read.table("Data/Bycatch.txt", header = T)

boxplot(Bycatch~Trawl,data=Bycatch.df, horizontal=T,xlab="Bycatch (kg)")

boxplot(log(Bycatch) ~ Trawl, data = Bycatch.df, horizontal = T, xlab = "log(Bycatch)")

原始数据箱线图显示右偏，对数变换后分布更对称

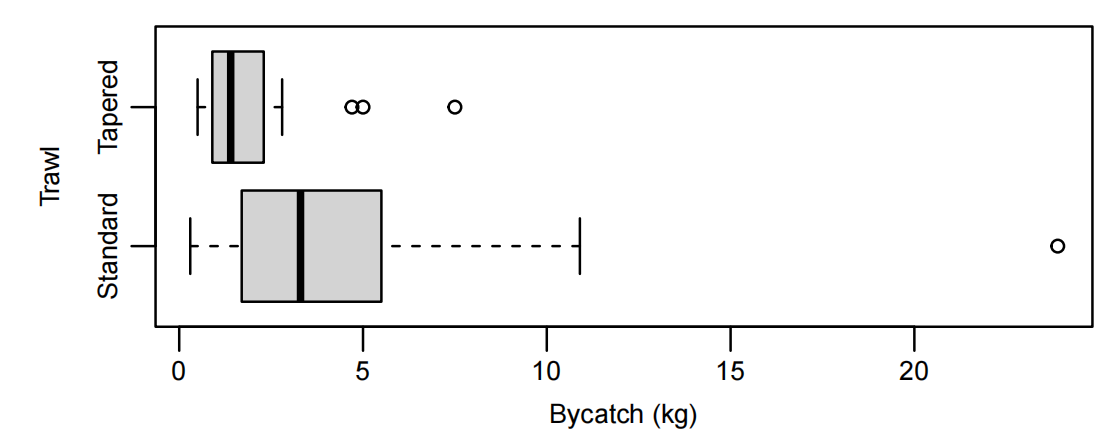
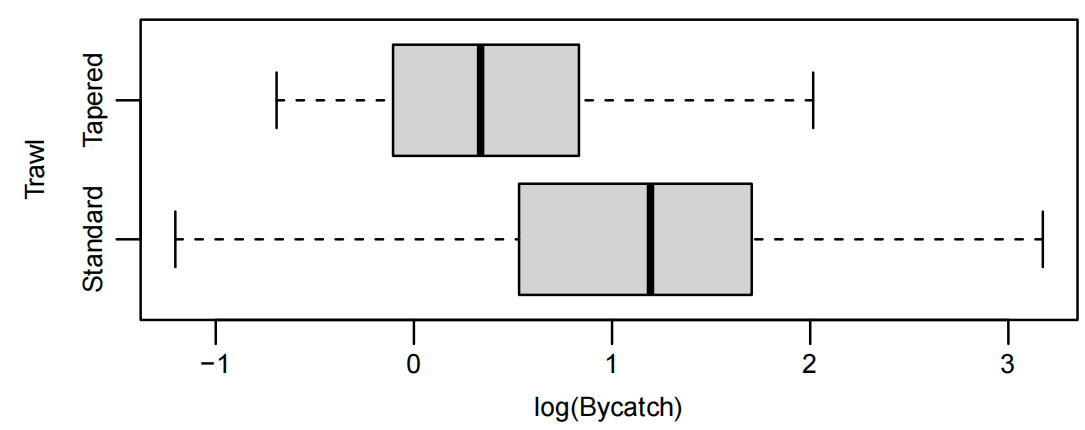
对数模型拟合：

以对数重量为响应变量，拖网类型为解释变量（锥形拖网为参照组）

Trawl.lmlog <- lm(log(Bycatch) ~ Trawl, data = Bycatch.df)

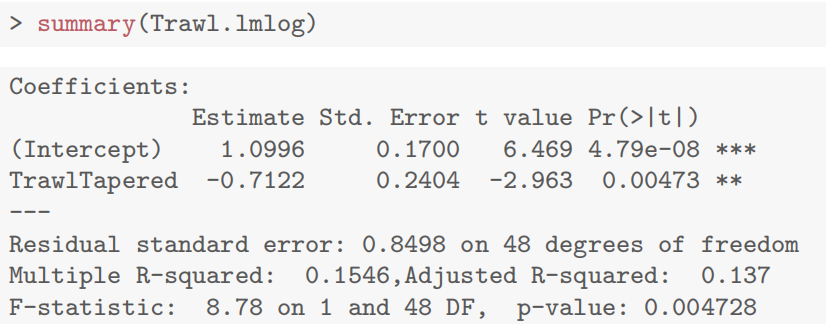
模型显示锥形拖网系数显著为负 ${\hat{β}}_{1} = - 0.7122$ ，表示其对数重量比标准拖网低 0.7122，对应原尺度中位数为 $e^{- 0.7122} \approx 0.49$ 倍（即减少 51%）。

结果解释

exp(confint(Trawl.lmlog))

锥形拖网副渔获物中位数为标准拖网的 30%~80%，即减少 20%~70%。

结论

锥形拖网显著减少副渔获物，乘法模型通过对数变换有效比较组间中位数倍数差异。

疑问：

1.什么是左偏 / 右偏？为什么均值大于中位数就是右偏？

偏态分布的定义（观察直方图得出，右偏就是数字大的点数量多，左偏就是数字小的点数量多）

右偏分布（正偏态）：数据的长尾在右侧（即右侧有少数极大值），直方图右侧延伸较长。例如房价、收入数据，少数极高值拉高整体均值，如奥克兰房价中，少数豪宅导致均值（1310.1）远高于中位数（1130）。

左偏分布（负偏态）：数据的长尾在左侧（即左侧有少数极小值），直方图左侧延伸较长。例如 “保质期” 数据，少数极短保质期拉低均值，此时均值 < 中位数。

均值 vs 中位数：偏态的 “指示器”

对称分布（如正态分布）：均值 = 中位数，两者重合，数据无偏。

右偏分布：均值 > 中位数。原因：均值对极端值敏感，右侧的极大值将均值 “拉向” 右侧，而中位数仅代表中间位置，不受极端值影响。例如，10 人收入数据：[1,2,3,4,5,6,7,8,9,100]，中位数是 5.5，均值是 15.5，均值被极大值 100 拉高。

左偏分布：均值 < 中位数。例如，数据[1,2,3,4,5,6,7,8,9,0]，中位数是 5，均值是 4.5，均值被极小值 0 拉低。

2.什么是乘法效应 vs 加法效应？为什么用 log 转换？

加法效应：解释变量（如年龄、拖网类型）每变化 1 单位，响应变量的绝对变化量固定。

例如：“年龄每增加 1 岁，工资增加 500 元”，即 $工资 = β_{0} + β_{1} \times 年龄$ ， $b e t a_{1}$ 是固定差值。

数据特征：散点图中，趋势线为直线，且数据波动范围（方差）不随解释变量变化而变化（等方差）。

乘法效应：解释变量每变化 1 单位，响应变量按固定比例变化（如折旧率、增长率）。

数据特征：散点图中，趋势线为曲线（指数下降 / 上升），且数据波动范围随响应变量增大而增大（异方差，如 Mazda 汽车价格随年龄增长，价格越低，波动越小）。

log转换：将乘法效应转化为加法效应，使指数关系线性化。

满足线性模型假设：对数转换后，数据更接近正态分布（解决右偏问题），且方差更稳定（等方差假设）。

便于解释：对数尺度上的系数 $β_{1}$ 表示比例变化，回transform后 $e^{β_{1}}$ 可解释为 “中位数乘以某一比例”（如年折旧率 15%）。

3.什么是回 transform 置信区间？为什么 exp 是 “回” transform？

Transform：从原尺度 y 到对数尺度 $l o g (y)$ （如 log(price)）是 “正向转换”。

回 transform：从对数尺度结果（如 $β_{0}$ 的 CI）通过指数函数 $\exp ()$ 转换回原尺度 y，是 “逆向转换”，因此称为 “回”。

4.什么时候需要用 log 转换？

数据右偏：当直方图显示右侧长尾（如房价、收入、销量），均值远大于中位数时，对数转换可使数据接近正态分布。

乘法效应：响应变量与解释变量呈指数关系（如折旧、增长、比例差异），对数转换可将指数关系线性化。

异方差：原始数据的方差随均值增大而增大（如 “价格越高，波动越大”），对数转换后方差更稳定。

5.该用log不用会有什么后果？

乘法效应的指数结构 与 线性模型的加法假设 不兼容，导致模型形式错误、方差非恒定、推断目标（均值 vs 中位数）偏离实际需求。因为s20x都是用最小二乘法拟合模型，这样就会出问题。

模型假设失效：无法满足线性模型的线性趋势和等方差假设，残差图出现曲线或漏斗状，拟合效果差。

效应解释错误：将比例变化（如折旧率、增长率）误判为固定差值，违背实际意义（如预测价格为负）。

推断不可靠：偏态数据导致均值受极端值影响，假设检验（p 值）和置信区间不准确，无法合理推断中位数。

第六章R语言代码总结

| 对数模型拟合 | model <- lm(log(y) ~ x, data = df) |
| --------------------- | --------------------------------------------------- |
| 回 transform 置信区间 | exp(confint(model)) |
| 残差图检查 | plot(model, which = 1) |
| 正态性检验 | normcheck(model) |
| 分类变量参照组设置 | df$group <- relevel(df$group, ref = "base_level") |

Case Study 6.1: Mazda price vs age

Problem

991年，《墨尔本时代报》收集了123辆马自达汽车的年龄和价格。我们希望了解马自达的价格及其随时间变化的情况。

测量的变量包括：

价格：以澳大利亚$为单位。

年份：制造年份（注意1990 = 90)。

Question of Interest

我们想看看马自达汽车的价格是如何随着年龄的增长而下降的。

Read in and Inspect the Data

Mazda.df=read.table("mazda.txt",header=T)

head(Mazda.df)

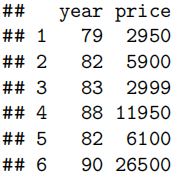
#我们需要创建一个名为age的新变量

Mazda.df$age=91-Mazda.df$year

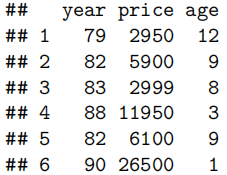
trendscatter(price~age,data=Mazda.df)

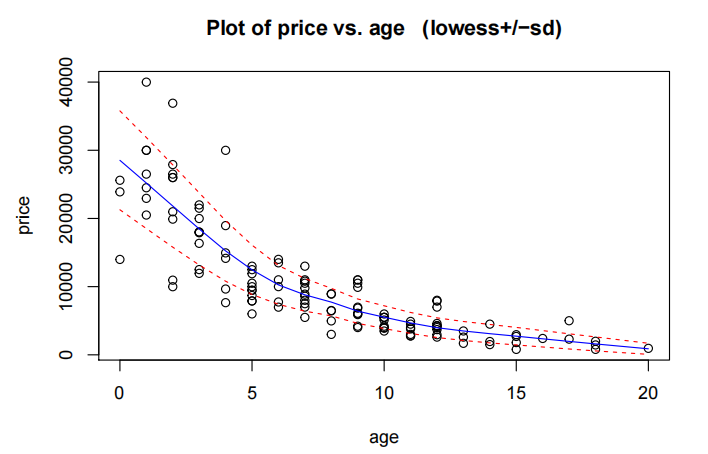
散点图显示了一种非线性的递减关系。随着年龄的增长，价格下降——但起初下降速度很快，随后逐渐放缓，最终继续下降。这表明存在指数递减的关系。

我们还发现，围绕趋势的离散度并不恒定：当价格较高时，离散度较大；而当价格较低时，离散度较小，因此较高的中心值与较大的离散度相关。

现在让我们使用年龄来拟合一个简单的线性模型。

Model Building and Check Assumptions

priceAge.fit=lm(Price~Age,data=Mazda.df)

plot(priceAge.fit,which=1)

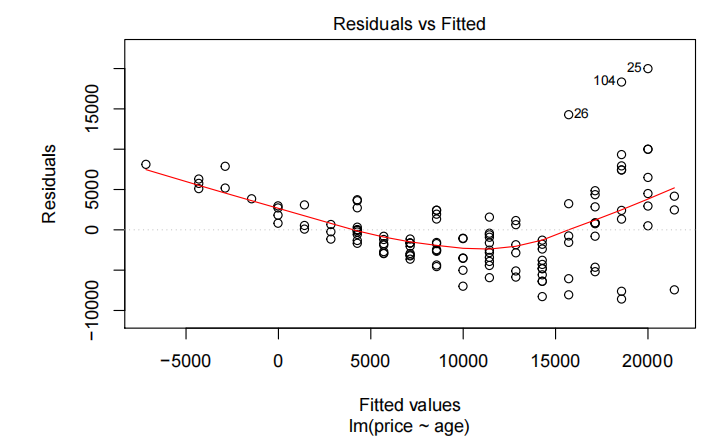
trendscatter(log(price)~age,data=Mazda.df)

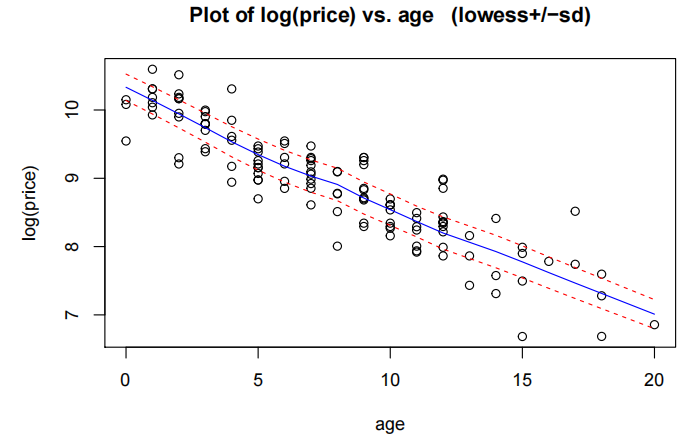
priceAge.fit2=lm(log(Price)~Age,data=Mazda.df)

plot(priceAge.fit2,which=1)

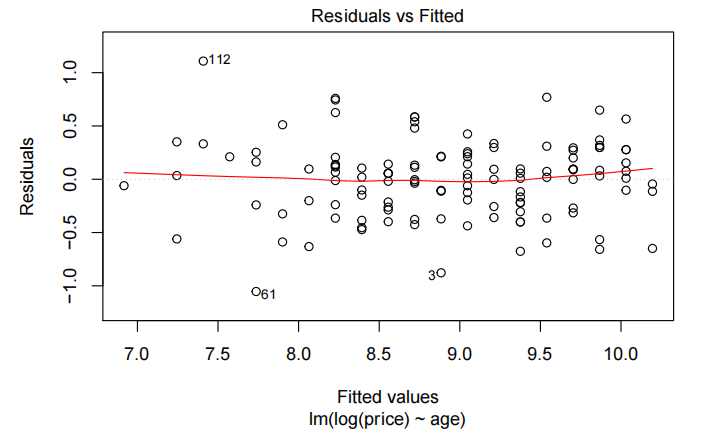
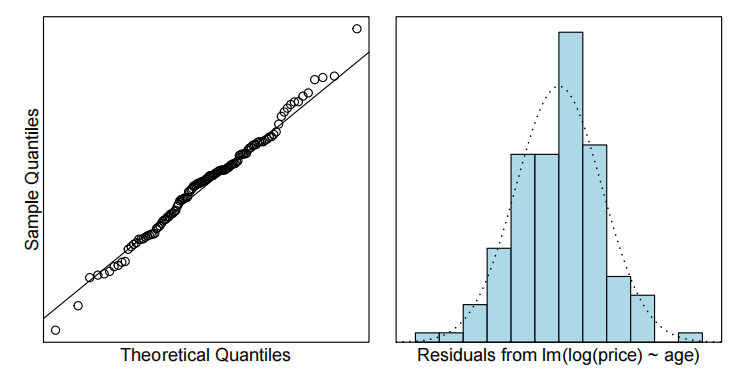
normcheck(priceAge.fit2)

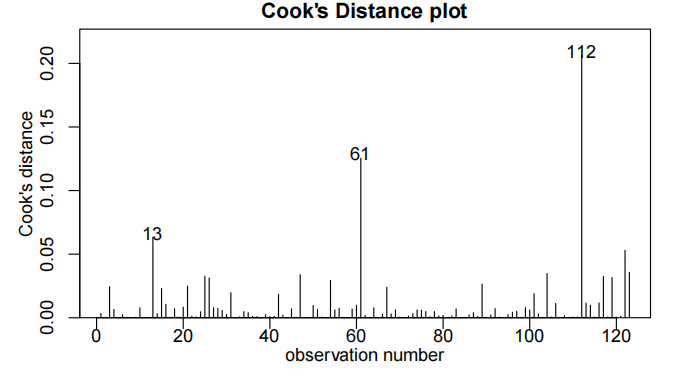
cooks20x(priceAge.fit2)

summary(priceAge.fit2)

Backtransform

exp(confint(priceAge.fit2))

*# Backtransform to % difference*

100*(exp(cinfint(priceAge.fit2))-1)

Method and Assumption Checks

年龄与价格的散点图显示了明显的非线性关系，并且随着价格的增加，变异性也随之增大。

简单线性模型的残差未能满足方差齐性和无趋势假设，因此对价格进行了对数转换。对对数后的价格进行简单线性拟合后，所有假设均得到满足。

我们的最终模型为

该模型解释了对数马自达价格变异性的82%。

Executive Summary

我们想看看马自达汽车的价格如何随车龄下降。

有明确的证据表明，随着车辆老化，价格呈指数级下降（P值≈0）。

我们估计，1991年新款马自达汽车的中位价格在23,600澳元到30,400澳元之间（四舍五入至最近的100澳元）。

我们估计，每增加一年车龄，折旧率在13.9%到16.3%之间。

Case Study 6.2: Students’ expenditure on haircuts by gender

Problem

感兴趣的问题是“女性是否比男性在头发上花费更多？”此外，“学生通常在理发上花费多少？”为了回答这些问题，一位讲师对200名学生进行了调查。同时，还测量了多种变量，包括头发和性别。

感兴趣的变量有：

头发：学生每月估计的理发支出。

性别：学生的性别，男性或女性。

Question of Interest

女性是否比男性在头发上花费更多？此外，学生通常在理发上花费多少？

Read in and Inspect the Data

survey.df=read.table("survey.txt",header=T,stringsAsFactors = T)

#为了使内容更加简洁，我们将数据单独放入了一个数据框中。

hair.df=with(survey.df,data.frame(hair=hair,sex=sex))

plot(hair~sex,data=hair.df)

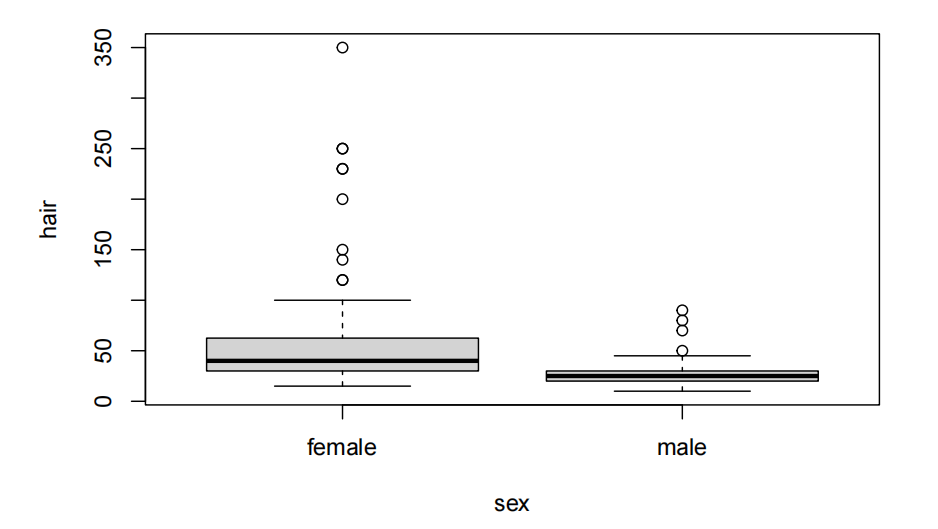
女性在理发上的花费似乎比男性多。数据显示，这一现象明显右偏（right-skewed）。此外，还存在方差齐性问题。或许取对数会有所帮助。

plot(log(hair)~sex,data=hair.df)

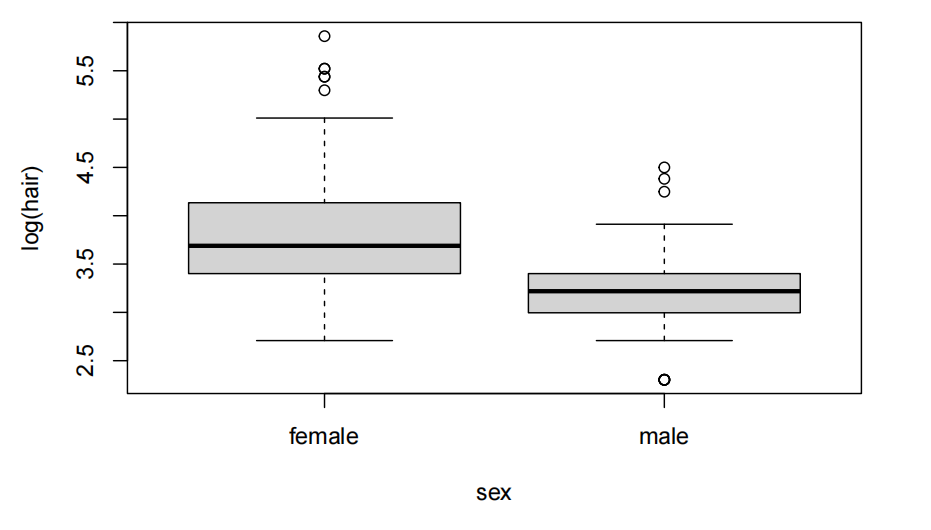
这确实让事情更美好，我们应该继续使用对数尺度。因此，我们或许应该在对数尺度上进行推断。即使在对数尺度上，女性似乎比男性在理发上花费更多。

Model Building and Check Assumptions

hair.fit<-lm(log(hair)~sex,data=hair.df)

plot(hair.fit,which=1)

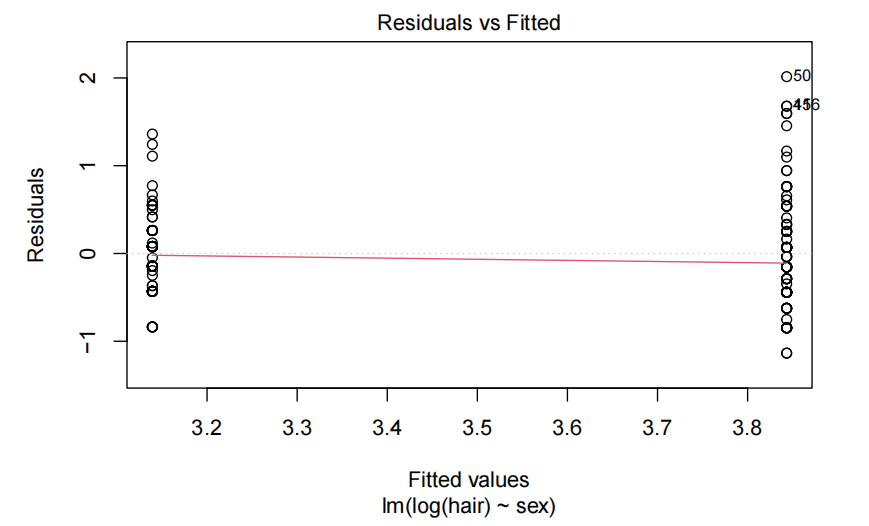
normcheck(hair.fit)

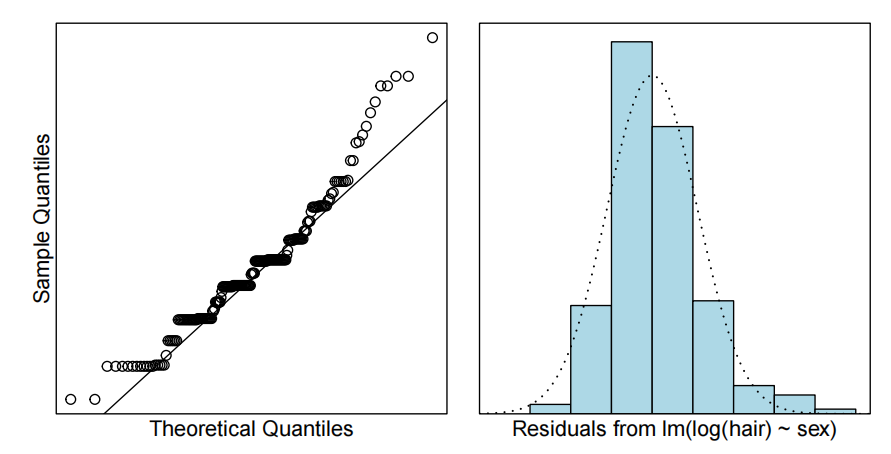
cooks20x(hair.fit)

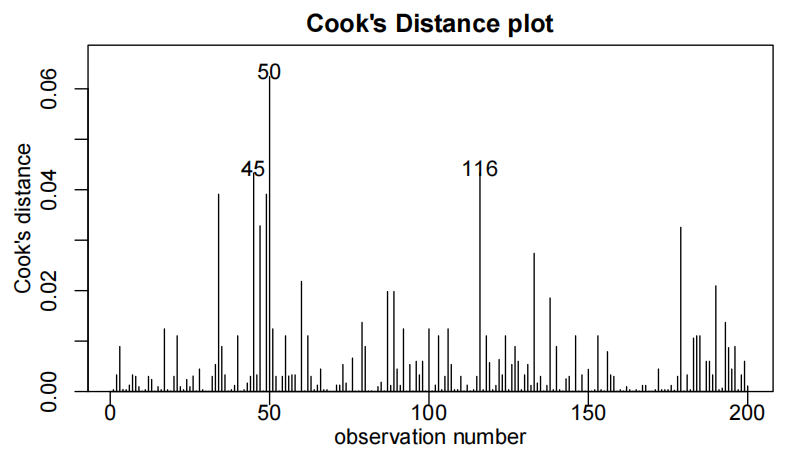
summary(hair.fit)

#将反变换后的输出列绑定在一起

cbind(exp(coef(hair.fit)),exp(confint(hair.fit)))

Confidence Interval Output

pred.df<-data.frame(sex=c("female","male"))

exp(predict(hair.fit,pred.df,interval="confidence"))

Methods and Assumption Checks

通过箱线图（boxplot）分析发现，头发长度与性别之间的数据呈现右偏态（right-skewed）分布。因此，我们对头发长度进行了对数转换处理（we log hair）。随后，对数转换后的头发长度与性别关系的箱线图显示出了显著改善。基于此，我们构建了一个线性模型，其中头发长度的对数值由性别因素解释。

我们可能不会从Q-Q图中认为数据是正态分布的。我们的数据显示，存在大量四舍五入的情况——人们将数值四舍五入到最近的5美元、10美元等。不过，CLT应该能够解决这个问题。残差的直方图呈现出单峰且相对对称的特征。因此，我们模型的其他假设也得到了验证。

我们的最终模型是： $l o g (H a i r_{i}) = β_{0} + β_{1} \times S e x M a l e_{i} + ε_{i}$

其中 $ε_{i} \sim i i d N （ 0 ， σ ² ）$ 分布。 $S e x M a l e_{i} = 1$ 表示学生为男性，否则为零。我们的模型解释了学生头发支出对数变化的29%变异性。

Executive Summary

我们有确凿的证据表明，女性通常在头发上的花费比男性多。

据估计，男性在头发上的花费大约是女性的一半。我们相信这一比例在42%到58%之间。

我们估计女性每月在头发上的中位（median）花费为47美元，我们相信这一数字在42至52美元之间。对于男性，我们估计每月的中位花费为23美元，我们相信这一数字在21至26美元之间。

Case Study 6.3: Students’ expenditure on clothing（可以不看）

Problem

研究关注的问题是“学生平均在服装上花费多少钱？”这一信息也记录在案例研究6.2中讨论的调查中。调查中测量了多种变量，包括服装。

感兴趣的变量是：衣服：学生每月在衣服上的估计支出。

Question of Interest

学生平均在衣服上花多少钱？

Read in and Inspect the Data

survey.df<-read.table("survey.txt",header=T)

#为了使内容不那么杂乱，我们将数据放在自己的数据框中。

clothes.df<-with(survey.df,data.frame(clothes=clothes))

hist(clothes.df$clothes)

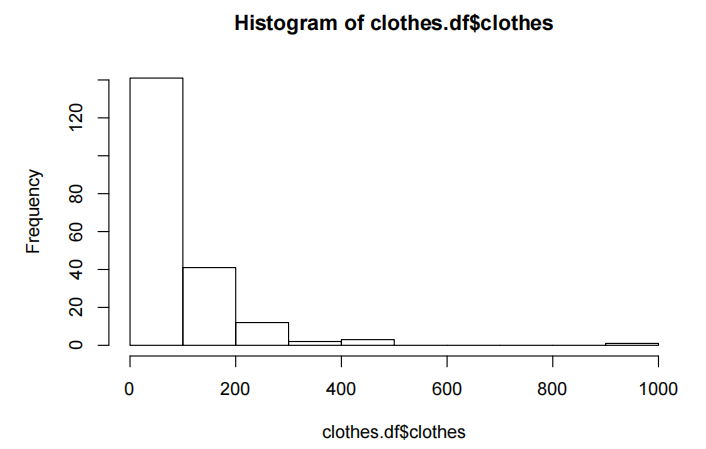
我们可以看到数据是相当右偏（right-skewed）的。对于这种偏斜的数据，中位数（median）似乎是一个更好的中心度量。对数据进行对数转换应该会有帮助。看起来还有一个非常“愚蠢”的值。也许我们应该省略它？

subset(clothes.df,clothes>800)

## clothes

## 15 999.99

这显然是一句“笑话”。让我们把它从进一步的分析中去掉。它不太可能产生什么影响，但我们认为这不是一个真正的答案，所以不妨把它去掉。

clothes.df<-subset(clothes.df,clothes<999)

hist(log(clothes.df$clothes))

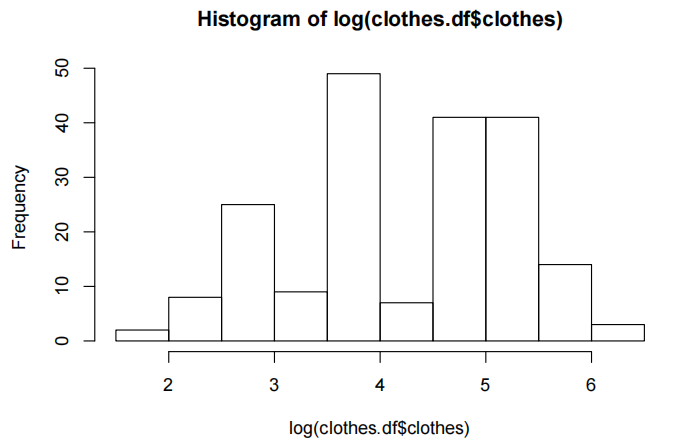
这或许让数据更加对称，但这是正常的吗？这里存在多个模式。让我们看看忽略这一点会发生什么。

Model Building and Check Assumptions

在 R 语言的线性模型公式里，~1这种表示方法意味着只包含截距项，而没有其他自变量。

clothes.fit<-lm(log(clothes)~1,data=clothes.df)

normcheck(clothes.fit)

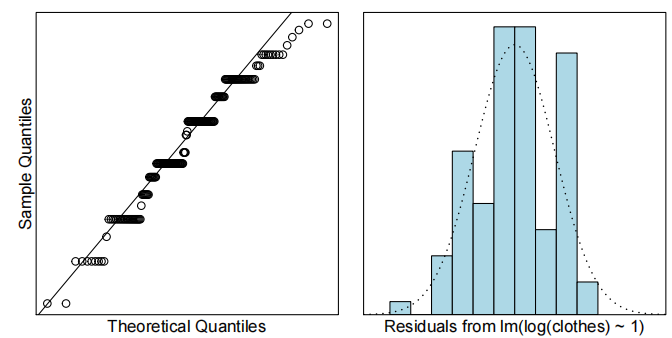
关于正态性呢？大量重复值——这在Q-Q图中表现为“阶梯”模式，而在残差图中则出现多个峰值。但CLT能帮我们解决这个问题吧？

exp(coef(clothes.fit))

## (Intercept)

## 70.38002

exp(confint(clothes.fit))

## 2.5 % 97.5 %

## (Intercept) 61.53073 80.502

median(clothes.df$clothes)

## [1] 85

哦，天哪！我们的样本中位数超出了置信区间。或许我们应该放弃正态理论，转而尝试自举法？请注意：要执行下一步，你需要安装bootstrap包。你可以在R代码块的开头取消注释（移除#）来完成这一步。只需做一次，之后它就会永久安装。因此，在第一次编译文档后，记得重新加上#。

# install.packages("bootstrap")

library(bootstrap)

m=bootstrap(clothes.df$clothes,10000,median)$thetastar

quantile(m,c(0,025,0975))

## 2.5% 97.5%

## 50 100

这确实好一些，但真的好吗？这是我们的自助中位数分布。

hist(m)

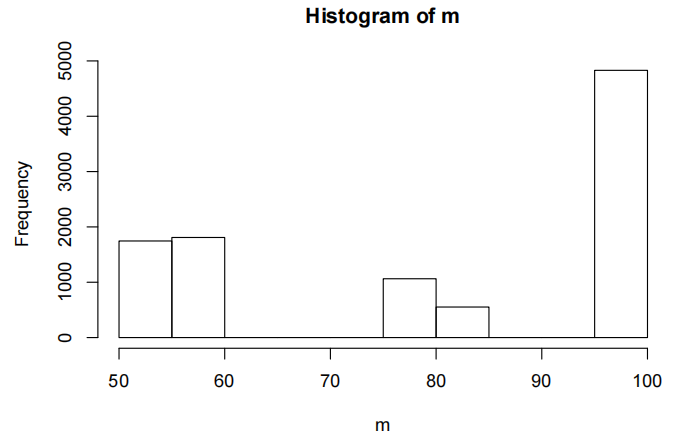
你愿意给出这个置信区间吗？大概不会吧。这就是我们说推断是近似的缘由。当我们对反变换后的对数数据进行推断时，实际上是在做关于几何平均数的推断。这定义为：

不难证明这两个公式在代数上是等价的，但第二个公式在数值过大时更容易出现计算溢出。只要样本量足够大，这种情况就会发生，前提是大多数x值都大于1。

因此，我们需要简要检查一下关于几何平均数的推断是否更有意义。R没有内置这个函数，所以我们需要自己定义它。

# Define the geometric mean for later on

geomean = function(x) {exp(mean(log(x)))}

我们所需要做的就是确保我们的几何平均值a）在置信限内，b）在原始尺度上的位置相同。

hist(clothes.df$clothes)

abline(v = est, col = "blue", lwd = 2)

abline(v = ci, col = "red", lty = 2, lwd = 2)

*# If this is correct, then the blue line should be replaced by a green line*

*# I've made it width 1, so you might be able to see it is right in the middle*

*# of the estimate, exactly where it should be*

abline(v = geomean(clothes.df$clothes), col = "green")

*# This is the median*

abline(v = median(clothes.df$clothes), col = "purple", lwd = 2)

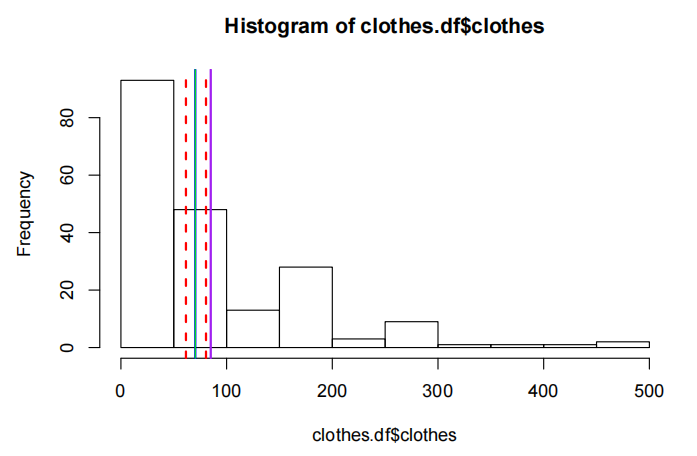
几何平均数在这里似乎更为合适。因此，这个例子强调了为了使这种近似推断有效，数据在对数尺度上必须呈正态分布。需要注意的是，无论怎样，这种方法都适用于几何平均数，但这一点在本课程中不会被考察。

Case Study 6.4: Clouding seeding

Problem

本问题的数据来源于一项实验，旨在验证人工增雨的效果。人工增雨是指将硝酸银（硝酸银）喷入云层，使水在硝酸银颗粒周围凝结，希望这些水滴能够聚集到足够大的体积，从而形成降雨。本研究中的测量单位为英亩-英尺，即能够均匀填充一英亩土地至一英尺深度的水量。一英亩-英尺大约等于123,348,185.532升水。这些数据已收录于s20x库中。

感兴趣的变量包括：

雨量：总降雨量。
种子：一个具有两个水平的因子，即播种和未播种。

Question of Interest

我们希望看到人工降雨是否能产生更多的雨水。另外，播种和未播种的云的典型降雨量是多少？

Read in and Inspect the Data

data(rain.df)

boxplot(rain~seed,data=rain.df,horizontal=T)

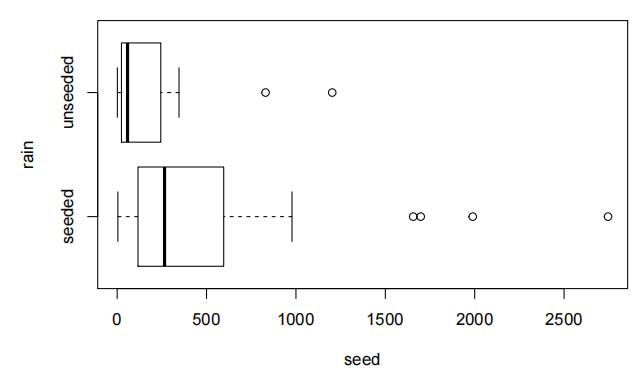
看起来又像是我们那个老右偏的朋友。也许，仅仅也许，对数转换会有效。让我们试试看。

boxplot(log(rain)~seed,data=rain.df,horizontal=T)

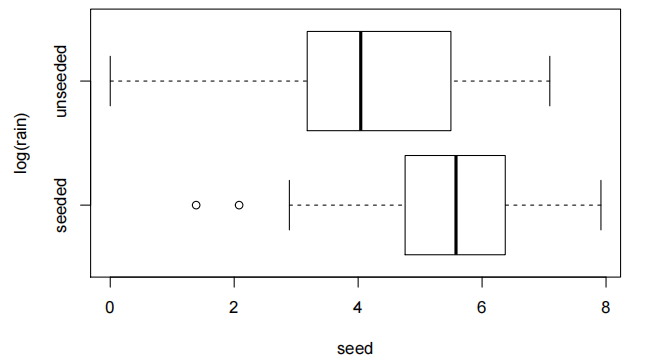
是的。看起来好多了，而且我们有初步证据表明播种似乎有效。我们应该担心方差的平等吗？

summaryStats(log(rain)~seed,data=rain.df)

不。在对数尺度上，标准差几乎相同，而中位数的差异远低于两倍。我们继续拟合模型。

Model Building and Check Assumptions

rain.fit<-lm(log(rain)~seed,data=rain.df)

plot(rain.fit,which=1)

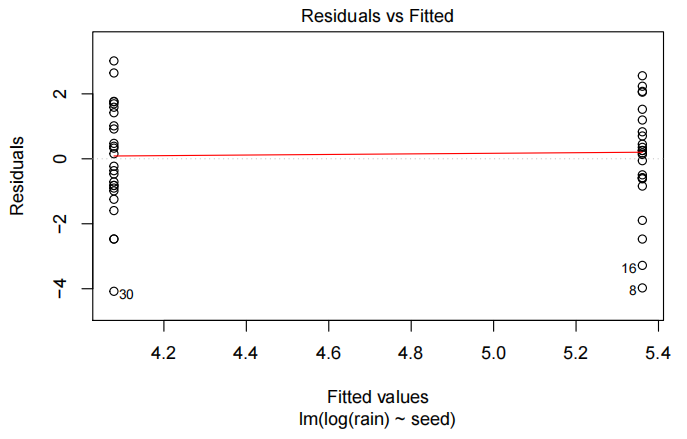
normcheck(rain.fit)

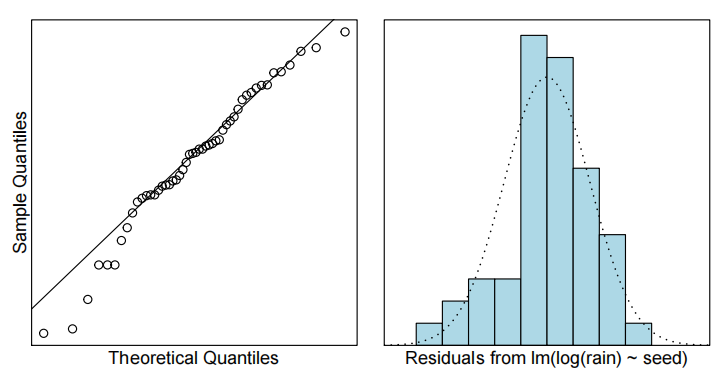
cooks20x(rain.fit)

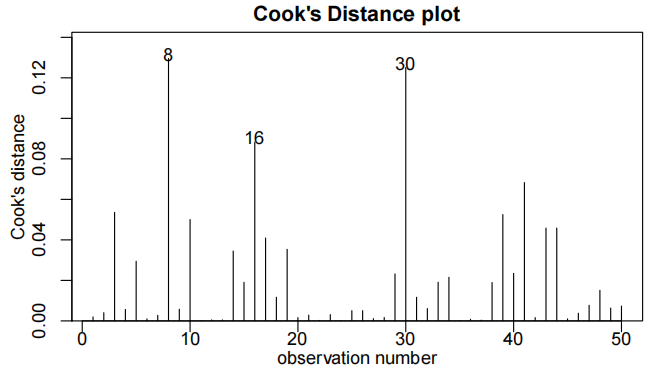
summary(rain.fit)

#让我们重新调整模型，使"未播种（unseeded）"成为基准水平。

rain.df$seed<-relevel(rain.df$seed,ref="unseeded")

rain.fit2<-lm(log(rain)~seed,data=rain.df)

summary(rain.fit2)

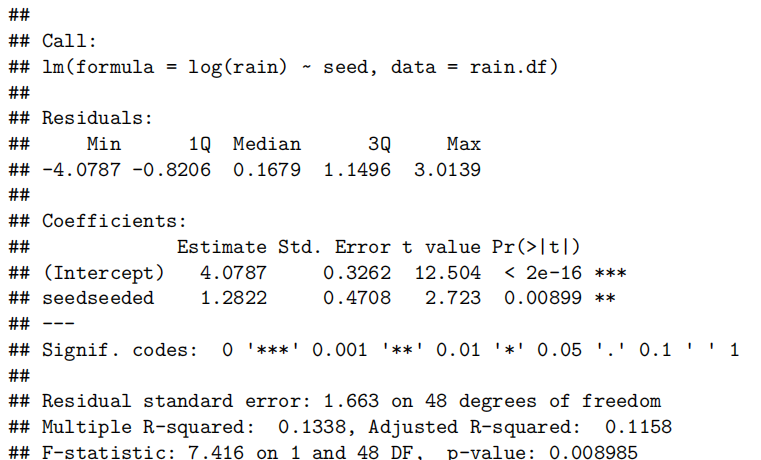
exp(confint(rain.fit2))

100*(exp(confint(rain.fit2))-1)

Confifidence Interval Output

pred.df<-data.frame(seed=c("unseeded","seeded"))

exp(predict(rain.fit2,pred.df,interval="confidennce"))

Methods and Assumption Checks

箱线图显示，各组的雨量对数值（log（rain））具有可比性。因此，我们通过线性模型来解释雨量对数值（log（rain））与种子因素之间的关系。

所有模型假设均得到满足。

我们的最终模型是: $l o g (R a i n_{i}) = β_{0} + β_{1} \times S e e d . S e e d e d_{i} + ε_{i}$

其中 $ε_{i} \sim i i d N （ 0 ， σ ² ）$ 。这里 $S e e d . S e e d e d_{i} = 1$ 表示观测是在有种子的环境中进行的，否则为零。

我们的模型描述了记录的总降雨量变化的13%。（describes 13% of the variability）

Executive Summary

我们想看看人工降雨是否能产生更多的雨水。

有强有力的证据表明人工增雨是有效的（P值小于0.01)。

我们估计，播种云的中位（median）降雨量比未播种云的中位降雨量高出约40%至830%。

未播种（人工降雨）的云产生的中位降雨量为30.7到113.8英亩英尺，而播种的云产生的中位降雨量为107.6到421.4英亩英尺。

Chapter 7: Power law linear models（幂律线性模型，也就是幂指数模型）

幂律模型的本质与适用场景

**模型定
义：幂律模型描述响应变量 y 与解释变量 x 的幂函数关系，形式为 $y = α x^{β}$ 。通过双对数变换转化为线性模型：（其中R语言里log就是以e为底，因为核心目的是非线性转为线性，谁为底问题不大）

$l o g (y) = β_{0} + β_{1} \log (x) + ϵ (β_{0} = \log (α), β_{1} 为幂律指数)$

这里其实是 $l o g (y) = l o g (α x^{β}) = l o g (α) + β l o g (x) = β_{0} + β_{1} l o g (x)$

核心思想：利用对数变换将非线性的幂律关系（乘法效应）转化为对数尺度上的线性关系（加法效应），适用于几何相似性问题（如体积与长度的关系）或比例变化场景。

最终目的是转化为线性模型后lm才是可以用的，才是有意义的

参数解释与推断

截距项 $β_{0}$ ：对应原尺度下 $y = α x^{β_{1}}$ 中的常数项 $α$ ，即 $x = 1$ 时的中位数估计。
斜率项 $β_{1}$ ：表示 x 每增加 1%，y 的中位数近似变化 $β_{1} %$ （通过泰勒展开近似： ${1.01}^{β_{1}} \approx 1 + β_{1} \times 0.01$ 。
假设检验：检验幂律指数是否符合理论值（如几何推导的 $β_{1} = 3$ ，使用 t 检验或置信区间判断显著性。

数据特征与模型假设

数据特征：散点图呈现曲线趋势，且方差随 y 增大而增大（异方差），对数变换后数据接近正态分布且方差稳定。
假设检验：通过残差图（plot(model, which=1)）检查等方差，normcheck(model) 检验正态性，cooks20x(model) 检测影响点。

例题：鲷鱼体重与长度的幂律关系

问题：通过鲷鱼长度预测体重，验证几何理论（体积与长度的 3 次方关系）。
数据：844 条鲷鱼的叉长（len, cm）和体重（wgt, kg），散点图显示非线性关系，符合幂律模型假设。

数据探索与变换：

绘制原始散点图，观察到体重随长度增长呈曲线趋势

Snap.df <- read.table("SnapWgt.txt", header = TRUE)

plot(wgt ~ len, data = Snap.df, xlab = "Length (cm)", ylab = "Weight (kg)")

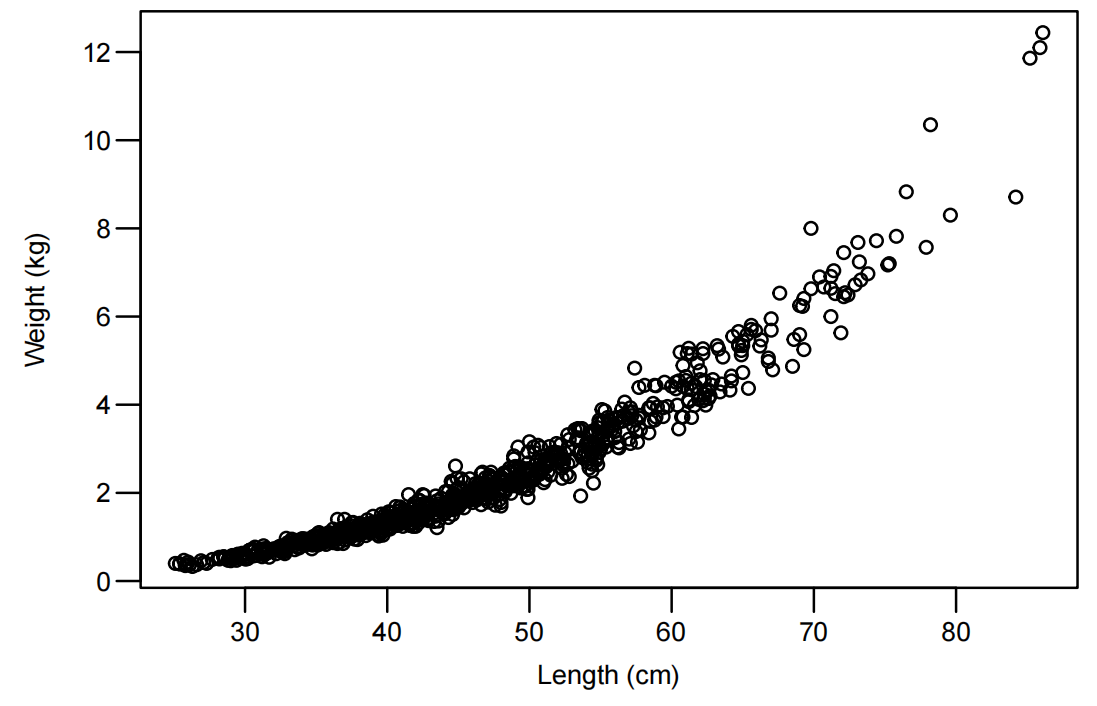
双对数变换后呈线性关系，绘制对数尺度散点图

plot(log(wgt) ~ log(len), data = Snap.df, xlab = "log(Length)", ylab = "log(Weight)")

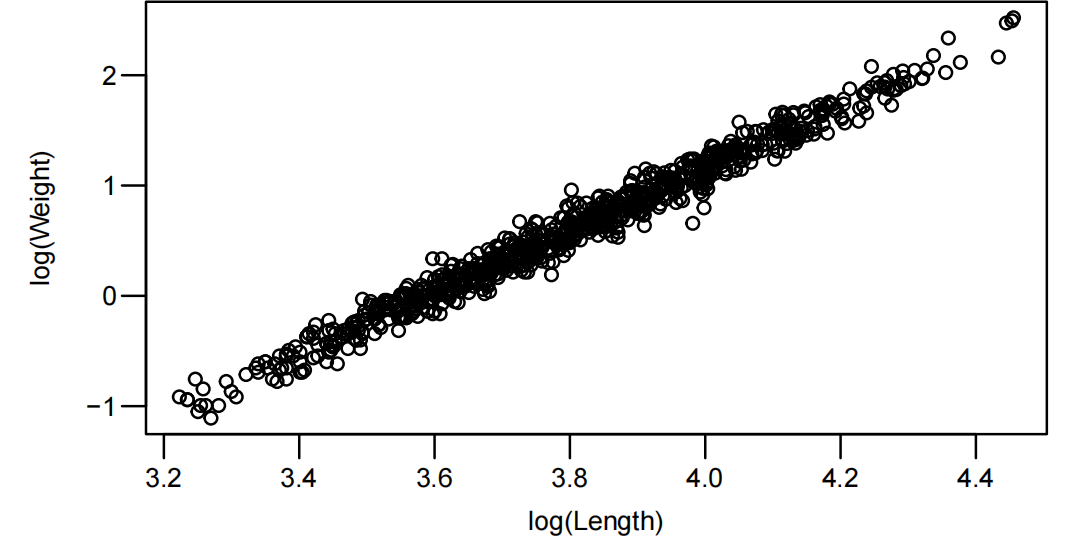
模型拟合与检验：

拟合双对数线性模型

Snap.lm <- lm(log(wgt) ~ log(len), data = Snap.df)

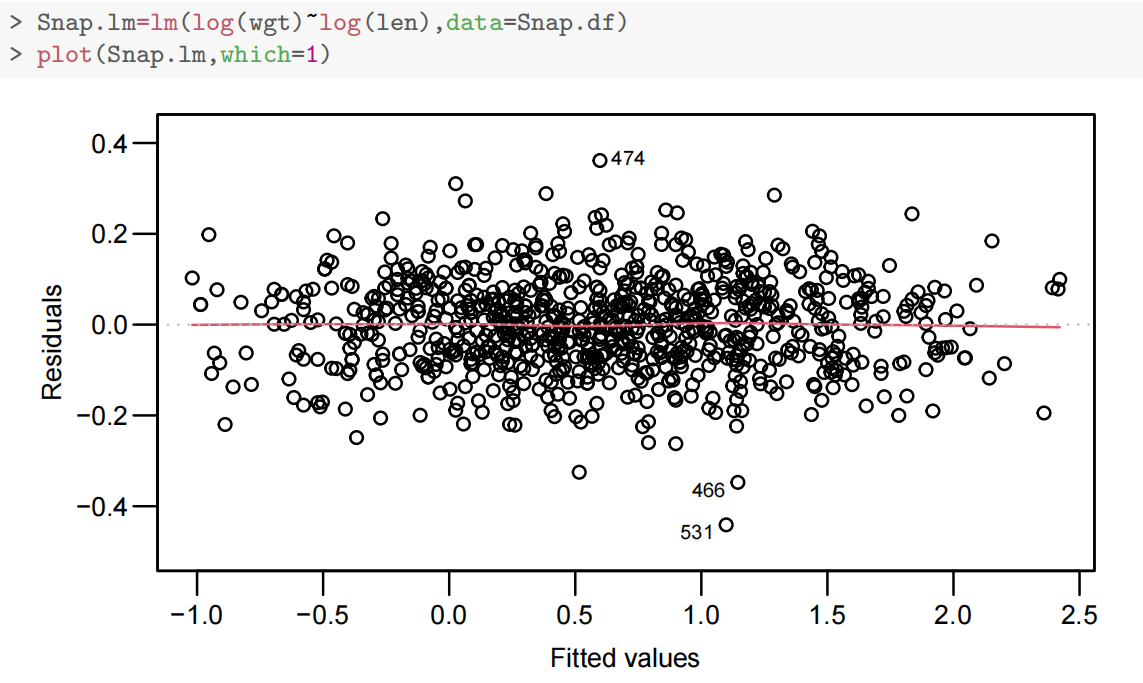
normcheck,cooks20x略

summary(Snap.lm)

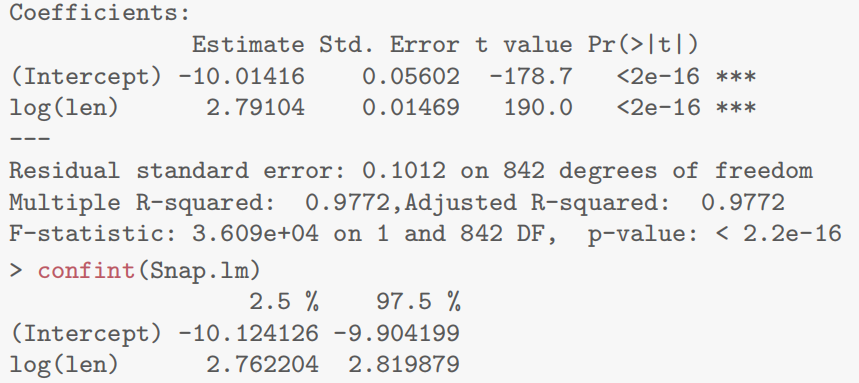
模型输出显示幂律指数 ${\hat{β}}_{1} = 2.791$ ，显著异于 0（(p < 2e-16)），置信区间为 [2.762, 2.820]，接近理论值 3 但存在差异。

预测与结论

Pred.df <- data.frame(len = 30)

exp(predict(Snap.lm, Pred.df, interval = "confidence"))

结果：中位数约 0.594 kg，95% CI 为 [0.586, 0.602] kg，验证了体重与长度的幂律关系。

结论：鲷鱼体重与长度符合幂律模型，幂律指数约为 2.79，略低于几何理论值 3，可能因体型差异导致。

第七章R语言代码总结

1.遵循幂律关系时对y和x取对数

Snap.lm=lm(log(wgt)~log(len),data=Snap.df)

2.用完log要还原回去 $b a c k t r a n s f o r m$ 预测

exp(predict(model, newdata = data.frame(x = x_value), interval = "confidence"))

或者先 $x x x . d f = d a t a . f r a m e (\dots = c (,,, \dots))$

Case Study: Power law model for cherry tree volumes

Problem

我们想建立一个模型，从树木的高度和直径测量中估计其体积。这个数据集提供了31棵被砍伐的黑樱桃树的直径、高度和木材体积的测量数据。

数据包括以下3个变量的31个观测值：

直径：以英寸为单位的树木直径（测量位置为地面以上4英尺6英寸）。

高度：以英尺为单位的高度。

体积：以立方英尺为单位的木材体积。

Question of Interest

其目的是能够根据树高和直径的测量值来估算树木的体积。

Model Justifification

利用基本几何学，可以认为体积与直径和高度之间存在幂律（Power Law）关系。具体来说，树干可以被合理地近似为圆柱体或圆锥体。

对于圆柱体，体积为 $V = π h r^{2}$ ，其中r是半径，h是高度。

对于圆锥，其体积为 $V = \frac{π}{3} h r^{2}$ 。

一般而言，这对应于幂律 $V \propto h d^{2}$ ，其中d是直径。

也就是说， $l o g (V) = β_{0} + l o g (h) + 2 * l o g (d)$ 。

可表示为 $l o g （ V ） = β_{0} + β_{2} * l o g (h) + β_{2} l o g (d)$ ，其中 $β_{1} = 1$ ， $β_{2} = 2$

因此，为了探索上述几何论证是否有效，我们还需要检验假设 $H_{0} : β_{1} = 1$ ， $H_{0} : β_{2} = 2$ 。

Read in and Inspect the Data

Cherry.df=read.table("Cherry.txt",header=T)

pairs20x(Cherry.df,c("volume","height","diameter"))

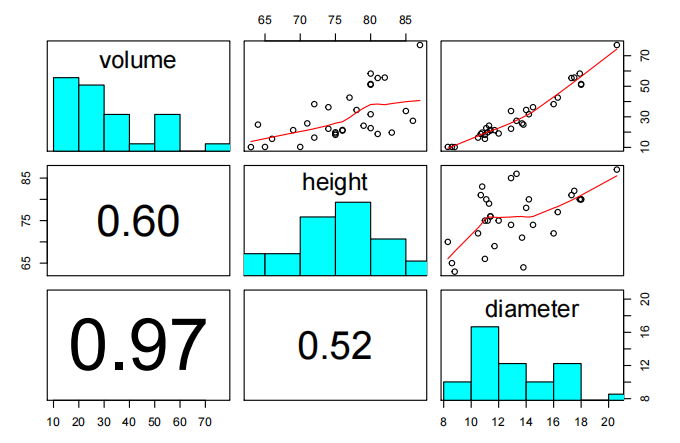
体积散射随尺寸增加。体积与高度之间的关系看起来接近线性，而直径与尺寸之间的关系看起来呈斜率增加趋势。

# Let's create some new variables in Cherry.df

Cherry.df$logvolume = log(Cherry.df$volume)

Cherry.df$logheight = log(Cherry.df$height)

Cherry.df$logdiameter = log(Cherry.df$diameter)

# Check out the new names

dimnames(Cherry.df)[[2]]

## [1] "diameter" "height" "volume" "logvolume" "logheight"

## [6] "logdiameter"

pairs20x(Cherry.df[,c("logvolume","logheight","logdiameter")])

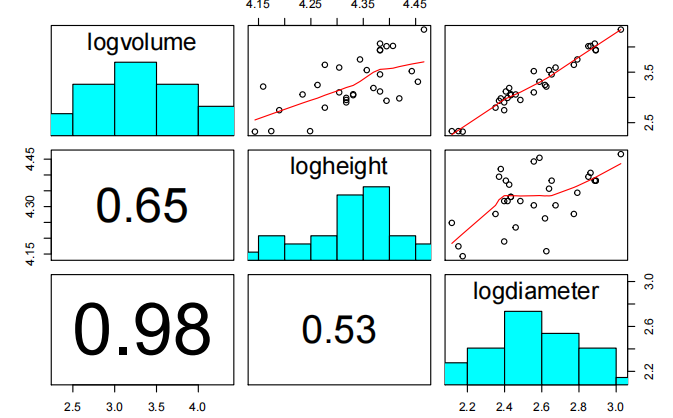
在logvolume中散射看起来是恒定的，与logheight和logdiameter的关系看起来是线性的。

Cherry.fit=lm(logvolume~logheight+logdiameter,data=Cherry.df)

plot(Cherry.fit,which=1)

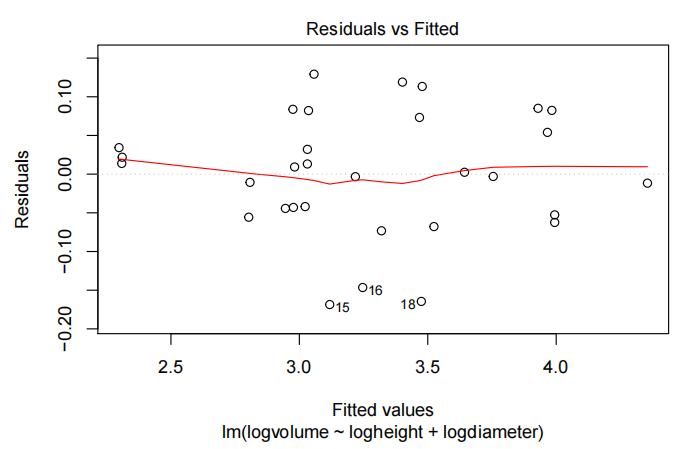
normcheck(Cherry.fit)

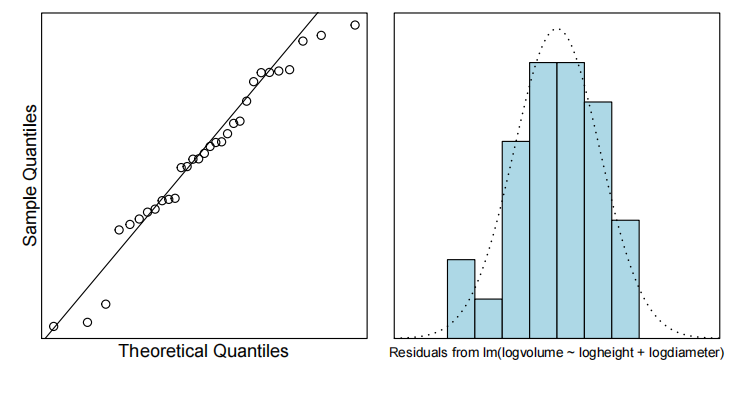
cooks20x(Cherry.fit)

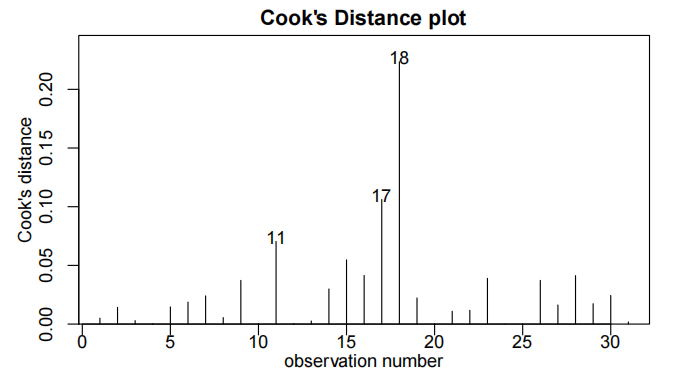
summary(Cherry.fit)

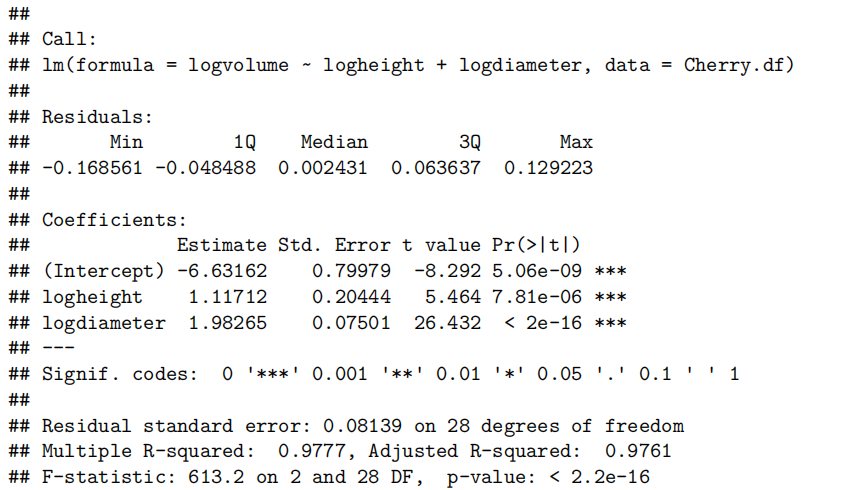
confint(Cherry.fit)

Test the Two Requested Hypotheses

# 获取感兴趣的估计值

(estimates = summary(Cherry.fit)$coeff[2:3, 1])

## 1.117123 1.982650

# 和它们相关的标准误差

std.errors=summary(Cherry.fit)$coef[2:3,2]

## logheight logdiameter

## 0.20443706 0.07501061

# 假设beta1=1和beta2=2的t value

tstats=(estimates-c(1,2)/std.errors)

## logheight logdiameter

## 0.5729066 -0.2313018

pvals=2*(1-pt(abs(tstats),28))

## logheight logdiameter

## 0.5712805 0.8187623

Method and Assumption Checks

在记录变量后，散点图显示了体积与高度和直径变量之间的预期线性关系以及恒定的散射。因此，我们拟合了一个幂律模型，用对数高度和对数直径来解释对数体积。

基本模型假设看起来是有效的，没有过分有影响力的因素。

我们的最终模型是

$l o g (v o l u m e_{i}) = β_{0} + β_{1} \times l o g (h e i g h t_{i}) + β_{2} \times l o g (d i a m e t e r_{i}) + ε_{i}$

其中 $ε_{i}$ ~ $i i d N (0, σ^{2})$

Executive Summary

目标是能够通过测量树的高度和直径来估算树木的体积。假设模型认为樱桃树的体积会与高度和直径呈幂律关系。具体来说，体积会随高度线性增加，同时与直径的平方成正比。

樱桃树的体积在高度和重量方面均遵循幂律模型，且没有证据表明这些幂值与假设的1（P值= 0.57 )和2（P值= 0.82 )不同。看来我们的几何论据是有效的。

我们估计，身高增加1%，中位体积（median volume）增加0.70%至1.54%，直径增加1%，中位体积增加1.83%至2.14%。

注意谈log的影响都要用median中位，因为log就是消除了这种非线性影响

Chapter 8: Linear models with both numeric and factor explanatory variables(具有数值和因子解释变量的线性模型)

模型结构与交互项引入

混合变量模型：同时包含数值变量（如测试成绩 Test）和二分类因子变量（如出勤率 Attend），模型形式为： $y = β_{0} + β_{1} x + β_{2} d + β_{3} x \cdot d + ϵ$

其中 $d$ 为因子变量的指示变量（0/1）， $x \cdot d$ 为交互项，表示数值变量在不同因子水平下的斜率差异。

交互项的意义与解释

无交互项 $β_{3} = 0$ ：数值变量的斜率在因子各水平下相同，仅截距不同（平行直线）。
**有交互项 $β_{3} \neq 0$ ：数值变量的斜率在因子各水平下不同（非平行直线），如出勤组的测试成绩对考试成绩的影响更显著。

假设检验与模型选择

交互项显著性：检验 $H_{0} : β_{3} = 0$ ，若显著则需分别解释各因子水平下的回归方程。
参照组设置：通过 relevel() 函数指定因子变量的基线水平（如以 “非出勤” 为参照，比较 “出勤” 组的差异）。

应用场景

分析不同群体（如性别、处理组）中连续变量的效应差异，如 “不同教育水平下工作经验对收入的影响是否不同”。

例题：Exam vs. test and attendance

问题提出

此案例旨在研究学生的测试成绩（Test，数值变量，范围 0 - 20 分）和出勤率（Attend，因子变量，分为出勤和不出勤）对考试成绩（Exam，数值变量，范围 0 - 100 分）的影响。重点关注测试成绩对考试成绩的影响是否会因学生的出勤情况不同而存在差异，即是否存在交互作用。

数据探索

为了直观观察不同出勤情况的学生中测试成绩和考试成绩之间的关系，绘制散点图。在散点图中，用不同的符号或颜色区分出勤和不出勤的学生。从图中可以初步看出，出勤组和不出勤组的测试成绩与考试成绩关系的斜率可能不同，这暗示着可能存在交互作用。

Stats20x.df <- read.table("STATS20x.txt", header = TRUE)

Stats20x.df$Attend <- as.factor(Stats20x.df$Attend)

plot(Exam~Test, data=Stats20x.df, pch = substr(Stats20x.df$Attend, 1, 1), col = ifelse(Stats20x.df$Attend == "Yes", "blue", "red"))

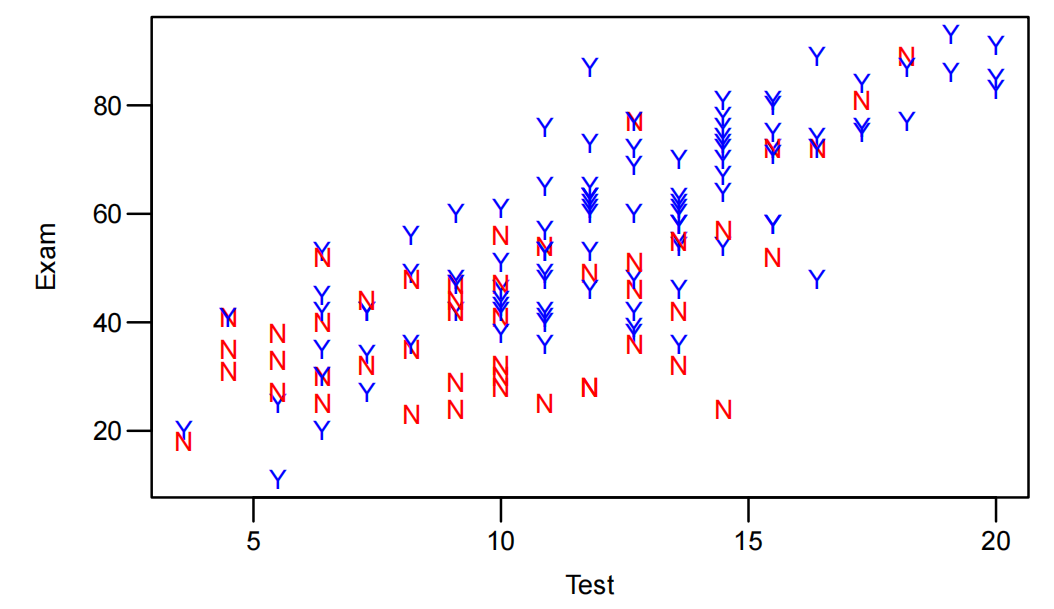
模型构建

无交互项模型：若不考虑交互作用，模型可以表示为： $Exam = β_{0} + β_{1} Test + β_{2} Attend + ϵ$ 在这个模型中，假设测试成绩对考试成绩的影响在出勤和不出勤组中是相同的，只是两组的截距可能不同。也就是说，无论学生是否出勤，测试成绩每增加 1 分，对考试成绩的提升幅度是一样的。
有交互项模型：为了检验是否存在交互作用，构建包含交互项的模型： $Exam = β_{0} + β_{1} Test + β_{2} Attend + β_{3} Test \times Attend + ϵ$

TestAttend.fit <- lm(Exam ~ Test * Attend, data = Stats20x.df)

这里的 Test * Attend 会自动包含 Test、Attend 以及它们的交互项 Test:Attend。

交互项的解释

交互项系数 $β_{3}$ 反映了出勤组和不出勤组中测试成绩对考试成绩影响的差异。如果 $β_{3}$ 显著不为 0，说明测试成绩对考试成绩的影响在两组之间是不同的。例如，若 $β_{3} > 0$ ，意味着出勤组中测试成绩对考试成绩的提升作用比不出勤组更大。

从 summary 输出中，我们可以按以下方式解读参数并写出拟合函数式：

截距项（Intercept）：估计值为14.4467，表示当 Test = 0 且 D = 0（不出勤）时，考试成绩Exam的预测值。
Test 项：系数为2.7496，表示不出勤组D = 0中，测试成绩每增加 1 分，考试成绩平均增加2.7496分。
D 项：系数为-4.2582，表示当 Test = 0 时，出勤D = 1比不出勤组的考试成绩预测值低4.2582分。
交互项 TestD：系数为1.1380，表示出勤D = 1中，测试成绩每增加 1 分，考试成绩比不出勤组多增加 1.1380分。

设 D 为出勤因子D = 1表示出勤，D = 0表示不出勤，Test 为测试成绩，拟合函数式为：

不出勤组D = 0： $Exam = 14.4467 + 2.7496 \times T e s t$
出勤组D = 1：

$\text{Exam} = (14.4467 - 4.2582) + (2.7496 + 1.1380) \times Test $

$= 10.1885 + 3.8876 \times T e s t$

Case Study 8.1: Exam vs attendance and test mark

Problem

我们之前分别使用了考试成绩和出勤率来解释考试成绩的差异，而这里的目标是将它们结合起来

Question of Interest

量化学生考试成绩与出勤率和测试成绩的关系。同时，考试成绩与测试成绩之间是否存在任何关系取决于学生是否参加了讲座。

Read in and Inspect the Data

Stats20x.df=read.table("STATS20x.txt",header=T)

plot(Exam~Test,data=Stats20x.df,pch=substr(Attend,1,1),cex=0.7,col=ifelse(Attend=="Yes","blue","red"))

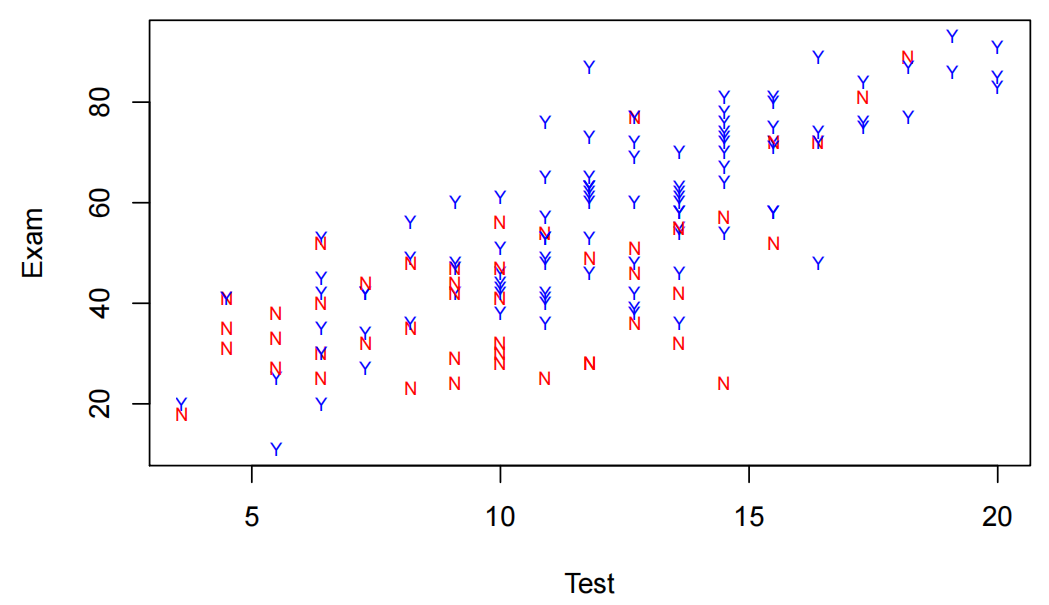
测试分数与考试的散点图表明，每个出勤组（“是”或“否”）的测试和考试之间的正相关关系是合理的线性关系，但两组的斜率可能不同。

Model Building and Check Assumptions

examTestAttend.fit=lm(Exam~Test*Attend,data=Stats20x.df)

plot(examTestAttend.fit,which=1)

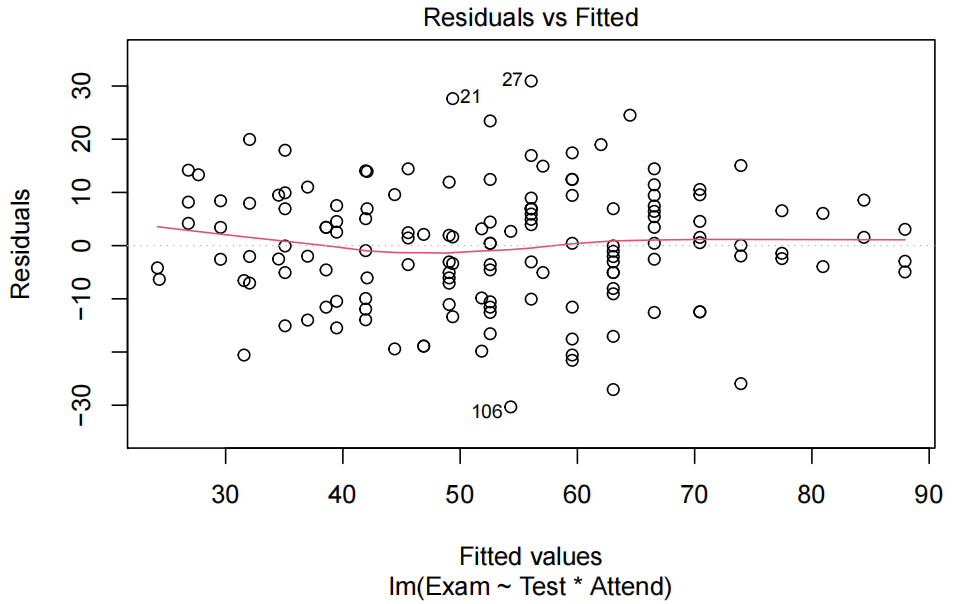
normcheck(examTestAttend.fit)

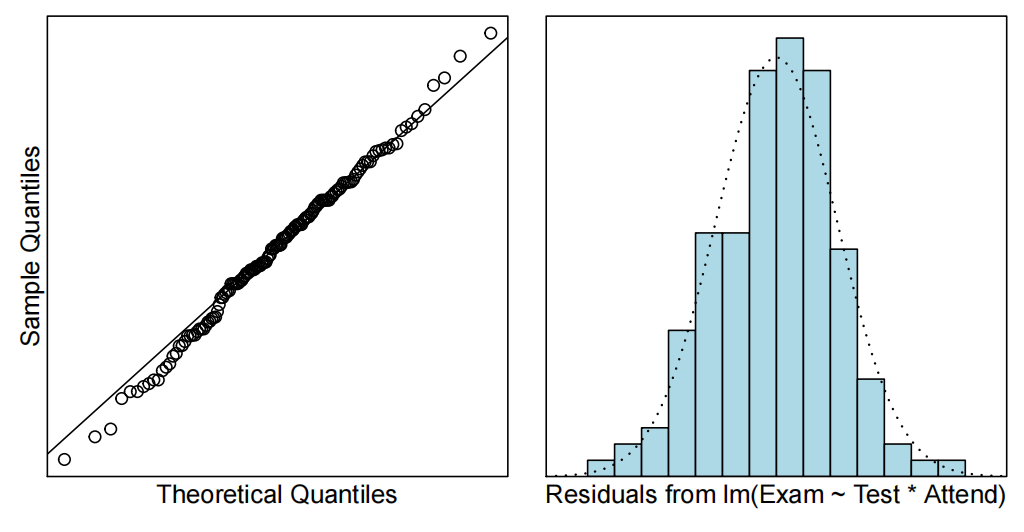
cooks20x**(examTestAttend.fit)

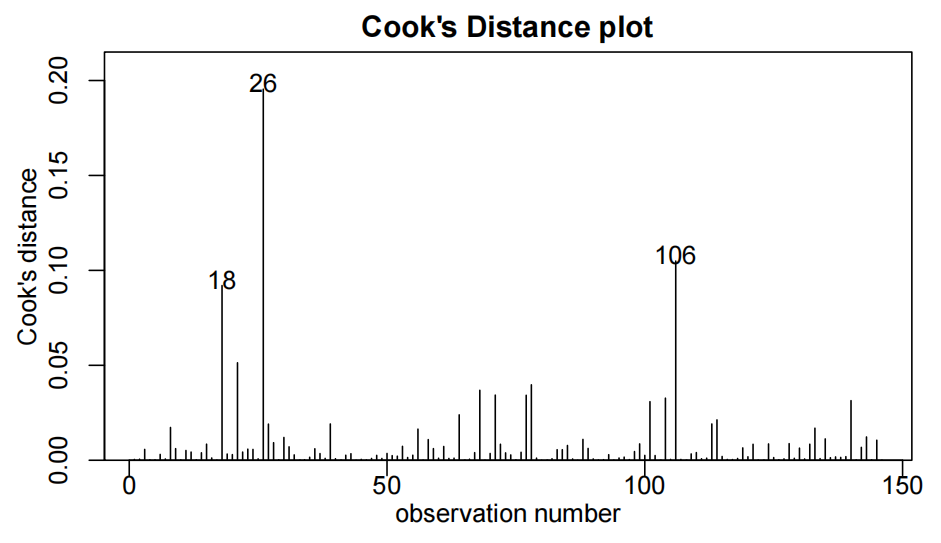
summary(examTestAttend.fit)

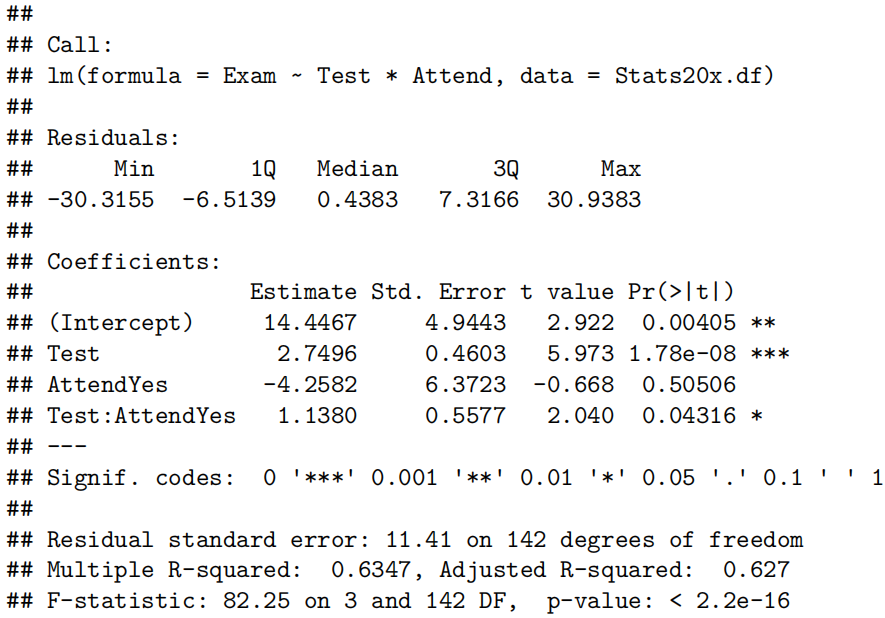
confint(examTestAttend.fit)

Visualise the Final Model

predAttend.df = data.frame(Test = 1:21, Attend = "Yes")

predSlackers.df = data.frame(Test = 1:21, Attend = "No")

plot(Exam ~ Test, data = Stats20x.df,pch = **substr(Attend, 1, 1), cex = 0.7, col = ifelse(Attend == "Yes", "blue", "red"))

lines(1:21, predict(examTestAttend.fit, predAttend.df), col = "blue", lty = 2)

lines(1:21,predict(examTestAttend.fit, predSlackers.df), col = "red", lty = 2)

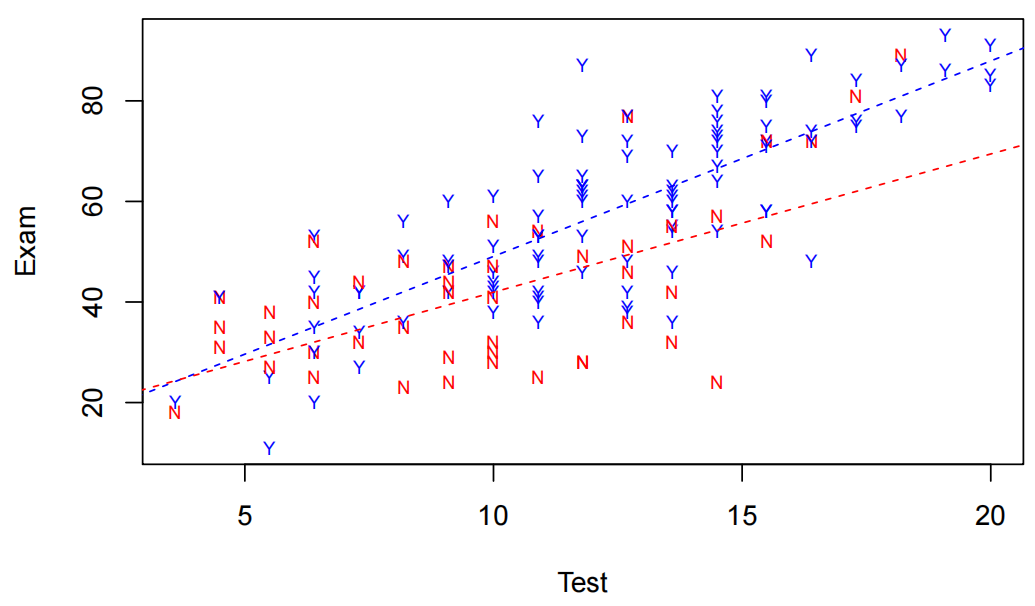
Method and Assumption Checks

由于我们有两个解释变量，一个数值变量和一个因子变量，因此我们拟合了一个线性模型，该模型使用了不同的截距和斜率来描述每个出席组（即交互作用模型）。我们不能删除交互作用项（P值= 0.043)。

所有模型假设都得到满足。我们的最终模型是

$E x a m_{i} = β_{0} + β_{1} \times T e s t_{i} + β_{2} \times A t t e n d_{i} + β_{3} \times A t t e n d_{i} \times T e s t_{i} + ε_{i}$

这里 $A t t e n d_{i} = 1$ 如果学生i是经常出席者，否则为0，并且 $ε_{i}$ ~ $i i d N (0, σ^{2})$

我们的模型解释了学生考试成绩变化的63%。

Executive Summary

我们想量化学生的考试成绩与出勤率和考试成绩之间的关系。

测试成绩与考试成绩之间存在明显的线性关系，但这种关系在参加讲座的学生和未参加讲座的学生之间有所不同。

我们估计，对于不参加讲座的学生，每多得一个测试分数（满分20分），其预期考试成绩会增加1.8到3.7分。

而对于经常参加讲座的学生，每多得一个测试分数，其预期考试成绩会额外增加0.04到2.2分。

Case Study 8.2: Refractive Index Calibration

请注意，本手册要求您在尝试示例之前安装dafs软件包

玻璃碎片对法医科学家来说非常重要。如果犯罪过程中窗户或其他玻璃制品被打破，那么微小的碎片可能会转移到破坏者身上。研究表明，来自同一来源的玻璃具有相似的折射率（RI），而不同来源的玻璃通常具有非常不同的折射率。因此，如果在嫌疑人的衣物上发现与犯罪现场破碎玻璃来源具有相似折射率的玻璃碎片，可以将该人与犯罪联系起来。

折射率描述了光从一种光学介质（如空气）进入另一种密度不同的介质（如玻璃或水）时的“弯曲”方式。如果你愿意思考这个问题，可以想象一下当你透过一杯水看到铅笔时，铅笔似乎被“切”成了两截。这是因为玻璃和水都比空气更密集。玻璃的折射率是通过将其置于硅油中测定的。硅油的光学密度可以通过加热或冷却来改变。将一块玻璃碎片放入硅油滴中，然后加热直到玻璃与油在光学上无法区分。记录下这一过程发生的温度。接着冷却硅油，并记录玻璃重新出现时的温度。这两个温度的平均值称为匹配温度。然后通过校准线将此匹配温度转换为折射率。校准是指使用一组已知Y值的标准品，通过仪器测量相应的X值的过程。这些值对可以用来生成校准曲线，该曲线可用于插值（或预测）观察到的X值对应的未知Y值。

在这个例子中，我们有一组12个已知RI值的标准品（标记为B1至B12）。每个标准品都由两位不同的法医科学家测量了多次，分别是Rachel Bennett（RB）和我的波兰同事Grzegorz“Greg”Zadora（GZ）。每位科学家对每个标准品的每次测量都记录了RI值和匹配温度。我们想知道这两个不同的实验室/科学家是否使用了两条不同的校准线。

data("ri.calibration.df")

## Let's make the name shorter so it is easier to work with ri.df = ri.calibration.df

names(ri.df)

## [1] "standard" "ri" "temp" "owner"

head(ri.df)

## standard ri temp owner

## 1 B1 1.52912 39.97 RB

## 2 B1 1.52912 39.90 RB

## 3 B1 1.52912 39.97 RB

## 4 B1 1.52912 39.70 RB

## 5 B1 1.52912 39.76 RB

## 6 B2 1.52381 54.50 RB

首先绘制数据。

plot(ri~temp,pch=substr(ri.df$owner,1,1),data=ri.df)

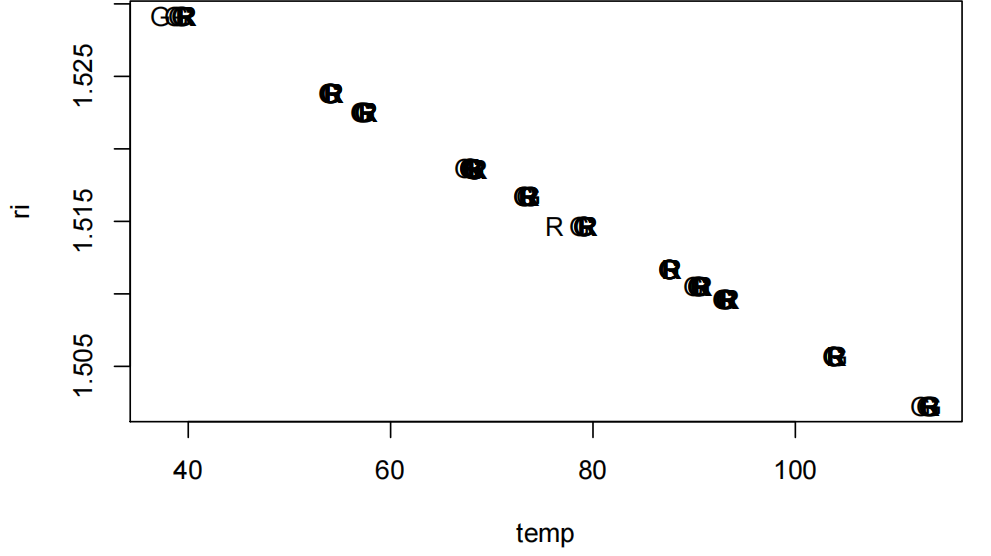
很难判断这个图是否有所不同。其中一个原因是这个数据非常精确。我们可以看到一些潜在的异常值。

我们将拟合一个模型。我们忽略在分析中对同一标准进行多次测量的事实。

ri.fit=lm(ri~temp*owner,data=ri.df)

eovcheck(ri.fit)

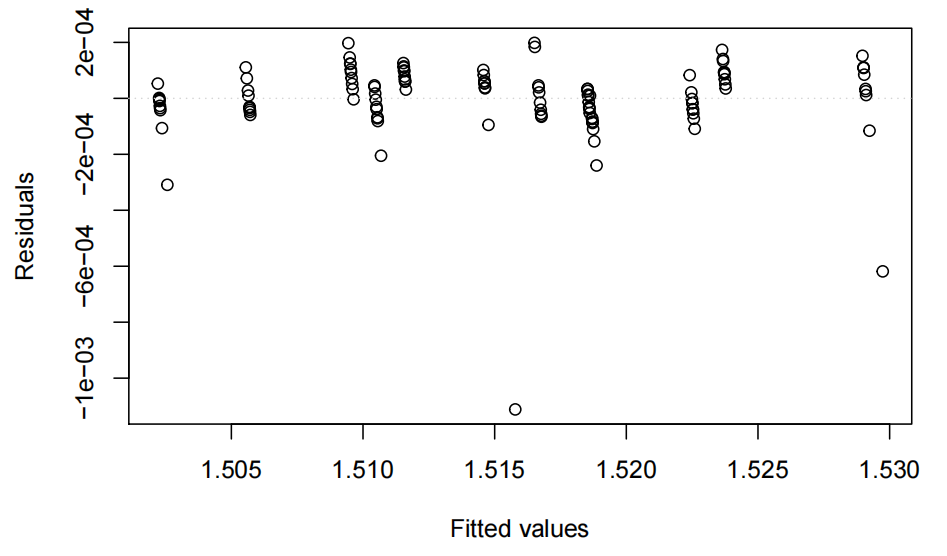
数据非常有规律性，我们之所以如此预期是因为每个标准都经过多次测量。我们可以看到有2-3个大的异常值，但总体来看方差的平等性看起来不错。

noemcheck(ri.fit)

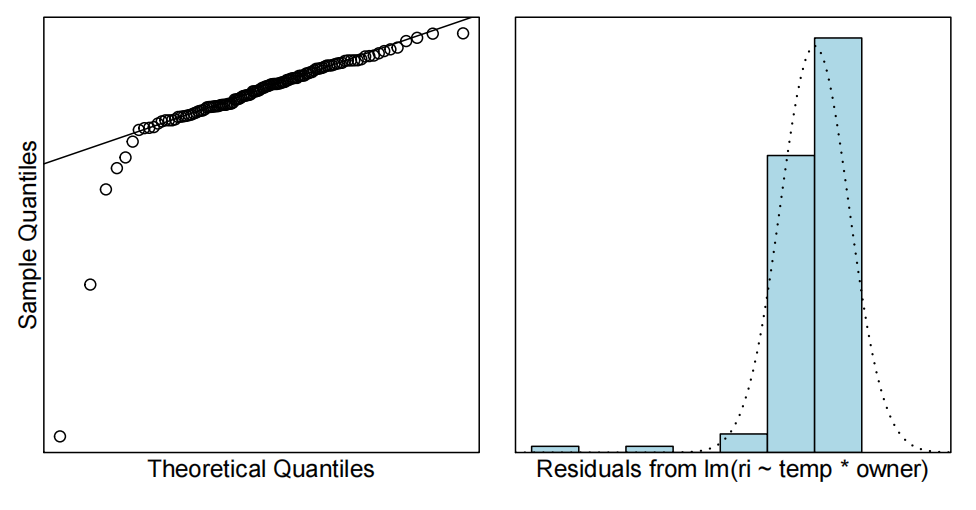
看起来又不错了，除了几个异常值。如果去掉第31和109点，情况会好很多。我们来试试看：

ri.fit2=lm(ri~temp*owner,data=ri.df,subset=-c(31,109))

normcheck(ri.fit2)

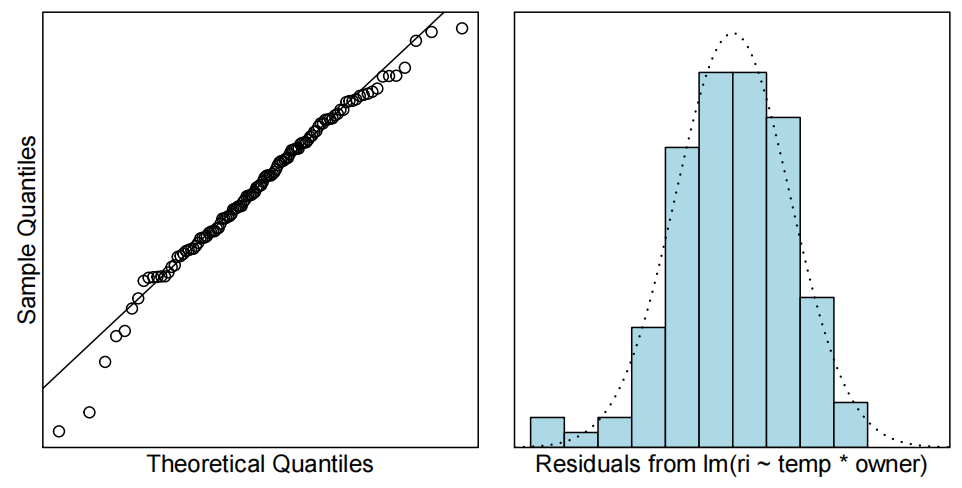
看起来好多了。图片没有被巨大的异常值扭曲。影响力点呢？我们真的期望有影响力点吗？

cooks20x(ri.fit2)

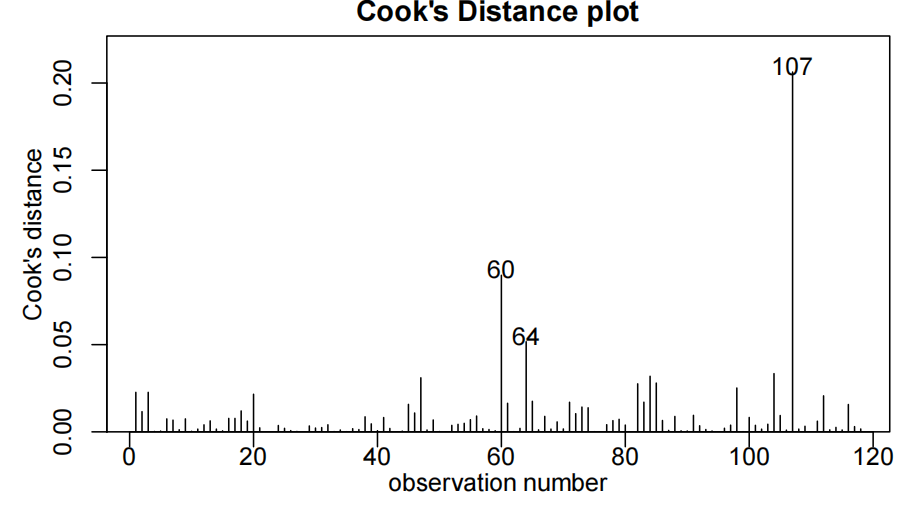
summary(ri.fit2)

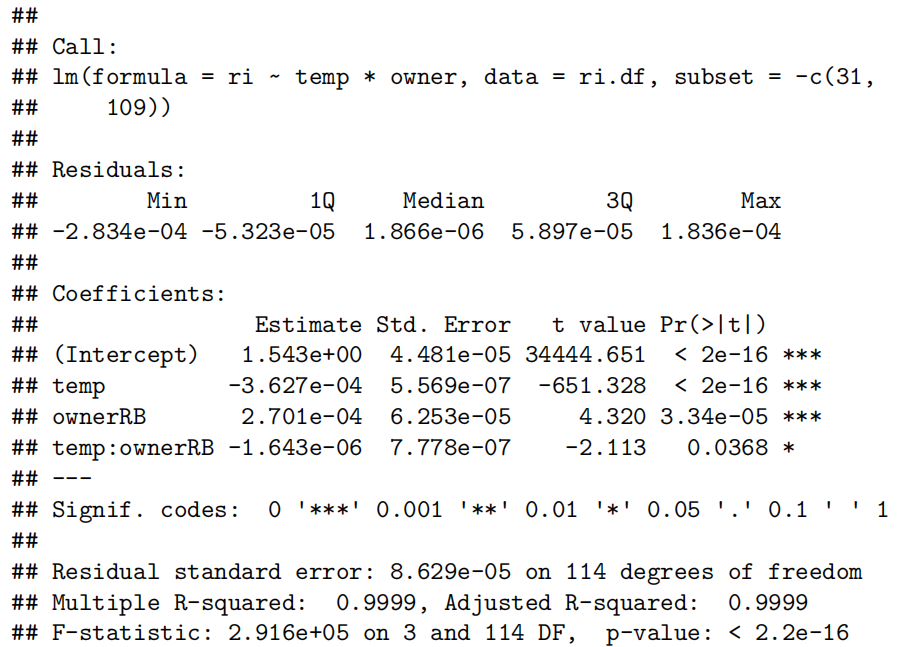
p=summary(ri.fit2)$coefficients[4,4]

b=coef(ri.fit2)

我们首先查看总体P值，该值非常小（< 2.2e-16）。这表明我们的变量在预测RI值方面很重要。

接下来，我们可以看到交互项temp：ownerRB具有显著性，P值为0.0368。因此我们有证据表明Rachel和Greg的校准线不同。Greg将使用拟合模型

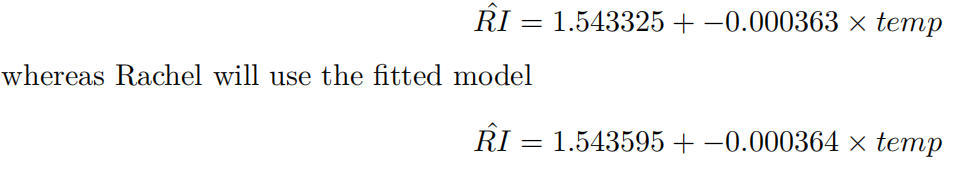
这些数值看起来非常接近，但在RI世界中，第四位到第六位的差异是至关重要的，所以这些线是完全不同的。您还可以看到，这是一个非常好的预测模型，因为R2接近1。

Test准备

第八周周一早八

考察题型：一共4道题，共计30分: 1判断题9分；2单选题4分；3.问答题 9分；4.问答题8分。英文作答，不能用中文。

1.理论基础辨析：（这部分要求线性回归的理论基础很清晰）

[!success]

1.模型设定与表达

基本模型公式：线性回归模型通常写为 y = β₀ + β₁x + ε。其中，β₀ 表示截距，β₁ 表示斜率，而 ε 为随机误差项，其期望值为0。

条件期望：模型假设解释变量 x 与响应变量 y 的关系体现在条件期望 E(y|x) = β₀ + β₁x 上，即在给定 x 的情况下 y 的“典型”值或平均值。

2.最小二乘估计（OLS）

估计方法：通过最小化所有观测值的残差平方和
∑₍ᵢ₌₁₎ⁿ (yᵢ − β₀ − β₁xᵢ)²
得到参数 β₀ 和 β₁ 的估计值，使得模型对数据的拟合误差最小。

数学推导Derivation：这一过程通常依赖于微积分和线性代数（如正规方程的推导），是理论证明与证明性质（如无偏性和最优性）的基础。

3.模型的基本假设
为了使OLS估计具有良好性质，线性回归模型通常需满足以下假定：

线性关系：响应变量和解释变量之间存在线性联系。

独立性：每个观测值（及其误差项 ε）相互独立，数据通常要求来自简单随机抽样。

同方差性（等方差，Homoscedasticity）：误差项的方差在所有 x 的取值上保持恒定，即 Var(ε) = σ²。

正态性：误差项近似服从正态分布，这对于构建置信区间和进行假设检验尤为关键。

4.参数解释与统计推断

参数解读：

截距 β₀ 表示当 x=0 时预测 y 的值；

斜率 β₁ 表示 x 每增加一个单位，预期 y 增加（或减少）的幅度。

假设检验与置信区间：

利用 t 检验对单个回归系数进行统计显著性检验；

利用 F 检验对整体模型是否显著进行检验；

构建各参数的置信区间，从而进行总体推断。

5.模型拟合优度与解释能力

残差分析：通过残差图（如残差对拟合值图）检查模型是否满足等方差性和线性假设。

决定系数（R²）：用以度量模型能够解释响应变量总变异的百分比，反映模型的拟合优度。

6.模型诊断与影响分析

异常值和杠杆点检测：识别那些可能对模型拟合产生较大影响的数据点。

Cook’s 距离：是一种常用的衡量单个观测值对整体回归系数影响程度的方法，帮助判断是否存在“影响点”（influential points）。

7.模型扩展及进一步讨论

多元线性回归：当存在多个解释变量时，模型表达为
y = β₀ + β₁x₁ + β₂x₂ + … + βₚxₚ + ε。

分类变量与交互作用：如何在模型中引入因子变量（如性别、类别等）以及解释交互效应。

模型选择与诊断改进：包括变量选择、模型转换（例如对数转换或其他非线性变换）等，以改善模型拟合和满足基本假设。

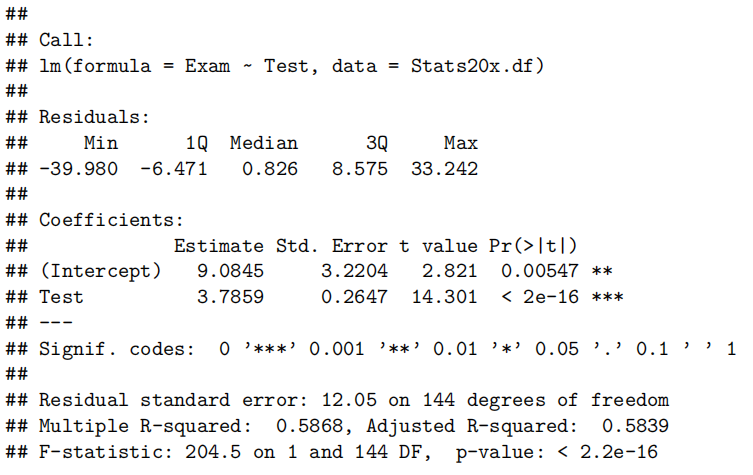
2.简单线性回归summary结果解释（所有的参数的理解，例如但不限于残差，自由度，p value, beta系数, 标准差，检验的假设, R^2等等）

[!success]

Call（模型公式）

Call: lm(formula = Exam ~ Test, data = Stats20x.df)

含义：这是拟合的模型公式，表明 Exam 作为响应变量（因变量），Test 作为解释变量（自变量）。换言之，我们要研究的是“期末成绩(Exam)”与“期中成绩(Test)”之间的线性关系。

Residuals（残差摘要）

Residuals: Min 1Q Median 3Q Max -39.80 -6.471 0.826 8.875 33.242

含义：这里给出了残差分布的五个数值摘要：最小值（Min）、第一四分位数（1Q）、中位数（Median）、第三四分位数（3Q）、最大值（Max）。

解释要点：

残差（Residual）：指观测值 $y_{i}$ 与模型预测值 ${\hat{y}}_{i}$ 之间的差，即 $r_{i} = y_{i} - \hat{y_{i}}$ 。

分布情况：如果模型合适且假设满足（如正态性假设），残差分布应大致对称，平均在 0 附近，无明显偏离。

最大/最小值：负残差意味着模型高估了真实值，正残差意味着模型低估了真实值。数值过大可能暗示有异常点或模型尚可进一步改进。

Coefficients（系数估计与显著性）

Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9.0845 3.2204 2.821 0.00547 Test 3.7859 0.2647 14.301 <2e-16 *

各列含义：

Estimate：回归系数的估计值

(Intercept)：截距项 ${\hat{β}}_{0} = 9.0845$ 。当 Test = 0 时，Exam 的预测值为 9.0845 分（可以理解为如果期中成绩是 0 分，期末预计能拿到 9 分左右）。

Test：斜率 ${\hat{β}}_{1} = 3.7859$ 。意味着 Test 每增加 1 分，则 Exam 的预测平均分增加约 3.79 分。

Std. Error：标准差（standard error）:测量系数估计值的不确定性；与抽样变动有关，数值越大表示估计越不精确。

t value：检验统计量

用于检验系数是否显著不同于 0（非0则变量对于响应变量具有统计显著影响）。

计算公式： $t = \frac{{\hat{β}}_{j} - β_{j}}{S E ({\hat{β}}_{j})}$ 。本来 $β_{j}$ 是根据题目要求得出，参数检验这里和0比较所以就是0了。

Pr(>|t|)：p 值

对应双侧检验下的概率，数值越小越说明该系数估计与 0 的差异显著；

若 p < 0.05（通常置信水平为 95%），可拒绝“该系数为 0” 的原假设，表明变量对于响应变量具有统计显著影响。

在此例中：截距和斜率的p值都非常小（尤其斜率小于 2×10^-16），说明这两个系数都在统计上非常显著，进一步验证 “期中成绩越高，期末成绩越高” 的线性趋势。

Signif. codes（显著性标记）

Signif.codes:0 ‘*’ 0.001 ‘’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

这是 R 默认的显著性标记方式。

*** 表示高度显著 (p < 0.001)

** 表示显著 (p < 0.01)

*表示相对显著 (p < 0.05)

. 表示接近显著 (p < 0.1)

空格表示不显著 (p ≥ 0.1)

在本例中，截距处有 “”，斜率处有 “*”，表示均非常显著。

Residual standard error（残差标准误）及 Degrees of freedom（自由度）

Residual standard error: 12.05 on 144 degrees of freedom

残差标准误 (Residual standard error)：12.05

这是残差的估计标准差，可视为“平均预测误差”的量度。数值越小通常表示模型拟合越好。

自由度 (Degrees of freedom)：144

若数据中有 n 个观测值，而且拟合了 2 个参数（截距和斜率），则残差自由度为 $n - 2$ 。

这里 df = 144，说明样本量 n = 146（即 146 条数据）。

R-squared（R²）与 Adjusted R-squared（调整后的 R²）

Multiple R-squared: 0.5868, Adjusted R-squared: 0.5839

Multiple R-squared (R²)：约 0.5868

R² 表示该回归模型能够解释的响应变量 Exam 的总体变异比例。

R² = 0.5868 说明约 58.68% 的期末成绩变异可以通过期中成绩的线性变化来解释。

Adjusted R-squared (调整后的 R²)：约 0.5839

在考虑解释变量数量后修正的 R²，防止随意增加自变量而导致的过高 R²。

对于只有一个解释变量的简单线性回归，R² 与 Adjusted R² 差别通常不大。

在只有一个解释变量的简单线性回归中，由于模型中参数较少，两者数值相差很小，一般可以直接引用 R² 来解释模型的拟合优度。不过如果是在比较不同模型时（即使只有一个解释变量），采用调整后的 R² 可能更稳健，因为它对模型的复杂度进行了调整，总体上在简单模型中二者意义相近，但一般写报告时直接引用 R² 就足够。

调整的R2考虑了自变量个数，如果两个模型的自变量个数一样，比较R2即可。不一样，就看调整的R2

F-statistic（F 统计量）与 Overall p-value（整体检验显著性）

F-statistic: 204.5 on 1 and 144 DF, p-value: < 2.2e-16

F-statistic：204.5

在简单线性回归中，F 统计量等价于 t 统计量的平方（只涉及单个自变量时）。

该数值越大，说明模型中该解释变量对响应变量的解释作用越明显。

p-value：< 2.2e-16

这是整体回归模型检验的显著性水平。p 值极小，远小于 0.05，表明整体模型非常显著，即我们有非常充分的统计依据拒绝“期末成绩与期中成绩无关”的原假设。

回归模型的整体解释

模型形式

模型： $\hat{E x a m} = 9.0845 + 3.7859 \times T e s t$

解释：当期中成绩为 0 分时，模型预测期末成绩约为 9.08；期中成绩每提高 1 分，期末平均成绩提高 3.79 分。

显著性

截距和斜率的 p 值都非常小（<0.01），说明在统计意义上二者都极为显著，不是偶然产生。

模型拟合优度

R² 接近 0.59，说明 “期中成绩” 这个单一变量可以解释期末成绩将近 59% 的波动。

模型的预测精度

残差标准误为 12.05，表示实际分数与模型预测分数平均相差约 12 分。

注意事项

虽然模型显著性和 R² 都不错，但我们仍需查看残差图、QQ 图等，以验证线性假设、同方差性和正态性等假设是否成立。如果存在显著异方差或非线性趋势，也可能需要对变量进行转换或考虑更复杂的模型。

预测区间与置信区间的差异：若要预测某个新学生的期末分数，需要使用预测区间（更宽）；若要估计均值，则使用置信区间（较窄）。

3.置信区间与预测区间的差别

[!success]

置信区间用于估计给定自变量值下的平均响应值（条件均值），而预测区间则用于预测单个新观测值，因包含个体误差，其区间更宽。

Confidence intervals estimate the average response at a given predictor value, while prediction intervals predict a single new observation and are wider because they account for individual variability.

4.会根据summary的输出，手动计算系数的95%置信区间。了解系数t检验的计算过程，会手动计算t-value，手动检验。

[!success]

参考图片输出内容（系数摘要）如下：

Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9.0845 3.2204 2.821 0.00547 Test 3.7859 0.2647 14.301 <2e-16 *

自由度 (Degrees of freedom)：144

若数据中有 n 个观测值，而且拟合了 2 个参数（截距和斜率），则残差自由度为 $n - 2$ 。

这里 df = 144，说明样本量 n = 146（即 146 条数据）。

显著水平: $α = 0.05$ （对应95%的置信区间）

手动计算 t-value（以斜率为例）

手动计算 t-value（以斜率为例） $t = \frac{\hat{β_{j}} - β_{j 0}}{S E (\hat{β_{j}})}$ ，就是

（估计值-特定值）/标准差

置信区间的通用计算公式

在回归模型里，对系数 $β_{j}$ 构建 95%置信区间通常采用：

$\hat{β_{j}} \pm t_{α / 2, d f} \times S E (\hat{β_{j}})$ ，其中

qt(0.975, df = 144)

点估计值就是estimate

t 检验的手动检验过程

判断t value（ $t = \frac{\hat{β_{j}} - β_{j 0}}{S E (\hat{β_{j}})}$ ）与基于显著性水平 $α = . . .$ 的t分位数 $t_{α / 2, d f}$ 的大小比较，如果t value大于 $t_{α / 2, d f}$ 那么就可以拒绝原假设。

5.回归模型的假设

6.模型应用：（所有分析命令和执行结果已给出，不需要写代码）

(1)根据散点图，选择适合的模型。

(2)模型最后拟合的公式。

(3)对数模型，自变量如何影响响应变量的变化。

(4)包含连续变量与分类变量的模型、交互效应判断、自变量如何影响响应变量的变化

(5)根据分析结果，写Executive Summary

[!success]

（5）答题要点

①我们想量化（quantify）一个…与…之间的关系

②…与…之间存在明显的（clear）线性关系，但这种关系…。

③我们估计（we estimate that）每多得一个…（each additional score）（通常对于结局对应状态）而对于…（特殊情况，比如说有经常参加讲座的，额外多多少）

Chapter 9: Linear models with both numeric and factor explanatory variables（具有数值和因子解释变量的线性模型）

Part 2: The model without interaction（无交互作用的模型）

本章以“学生语言成绩”作为响应变量，探讨其与数值型解释变量（如学生IQ）和因子型解释变量（如教学方法）之间的关系。

研究方法与目标

主要问题包括：

检验不同教学方法（因子变量）对语言成绩的差异是否显著；
是否需要考虑教学方法与IQ之间的交互作用；
如何利用置信区间给出差异范围（例如“95%置信区间：方法2比方法1高4.1至15.7分”）。

模型构建与选择

带交互项的模型

初步构建模型时考虑了IQ与教学方法之间的交互：

$l a n g = β_{0} + β_{1} I Q + β_{2} D_{2} + β_{3} D_{3} + β_{4} (I Q \times D_{3}) + β_{5} (I Q \times D_{3}) + ε$

其中，教学方法1作为基准（参考组）， $D_{2}$ （方法2相较于方法1）和 $D_{3}$ （）方法3相较于方法1分别为方法2和方法3的虚拟变量。

无交互（主效应）模型（Occam’s razor奥卡姆剃刀）

当交互项不显著时（例如通过ANOVA检验得知P值较大），可以简化为：

$l a n g = β_{0} + β_{1} I Q + β_{2} D_{2} + β_{3} D 3 + ε$

这种模型假设不同教学方法下IQ对语言成绩的影响（斜率）相同，但截距不同，从而形成“平行直线”。

因子变量的处理

数值型标签（如1、2、3）在R中默认会被识别为连续变量，而实际只是分类信息，所以应转换成因子（factor），让R正确创建虚拟变量。

如有需要，可通过relevel函数改变参考组，使得各组之间的比较更加直观。

结果分析与置信区间的解读

IQ效应：IQ的系数代表每增加1 IQ点时语言成绩的提升；乘以10后，可以解释每增加10 IQ点时成绩的改变范围（结合置信区间得出大约1.6到4.7分）。

教学方法效应：与基准组比较，因子虚拟变量的系数反映了不同方法之间平均差异；例如，方法2的系数说明在控制IQ的情况下，方法2的成绩比方法1高，其95%置信区间给出变化范围。通过改变参考水平，还可以直接比较方法2与方法3之间的差异。

例题分析：语言成绩与教学方法及学生IQ

总览：

变量类型与转换：

教材中使用的数据包含学生的语言成绩（lang）、IQ 与教学方法（method）。起初，method 被记录为数值（1、2、3），但这些数字仅为标签。为使 R 在建模时将其作为分类变量处理，需要将 method 转换为因子。

探索性数据分析：

绘制散点图（例如用 trendscatter() 或 plot() 函数），可观察到各教学方法下数据点大致沿平行直线分布，说明 IQ 对语言成绩的斜率在不同教学方法间相似，从而暗示交互项（即 IQ 与 method 的乘积项）可能不显著。

模型拟合与简化：

先拟合含交互项的模型lm(lang ~ IQ * method, data = teach.df)，检查各交互系数是否显著（教材例题中 P 值分别为 0.17042、0.38574）。由于交互项不显著，因此可以采用无交互项（主效应）模型：

$l a n g = β_{0} + β_{1} I Q + β_{2} D_{2} + β_{3} D_{3} + ε$ ，其中，D₂、D₃ 分别为教学方法 2 与 3 的虚拟变量，教学方法 1 为参考组。

结果解释（基于 95% 置信区间）：

IQ 的系数估计约 0.31564，意味着在相同教学方法下，每增加 1 个 IQ 点，语言成绩增加约 0.32 分；乘以 10 得到每增加 10 个 IQ 点时，成绩提高大致在 1.6 至 4.7 分之间。

方法 2 的系数大约为 +9.88，说明在控制 IQ 后，采用教学方法 2 的学生平均比采用方法 1 高约 9.88 分，其 95% 置信区间约在 4.08 至 15.68 分之间。

方法 3 的系数大约为 –14.16，说明在控制 IQ 后，采用教学方法 3 的学生平均比方法 1 低约 14.16 分，其 95% 置信区间约为 –20.02 至 –8.30 分。

如果更换参考组（例如将方法 2 设为参考组），可直接比较方法 3 与方法 2 的差异，教材得到的方法 3 与方法 2 的差异大约为 –24.04 分，其置信区间约为 –29.75 至 –18.32 分。

数据预处理与探索性绘图

导入数据并查看结构：

library(s20x) data(teach.df) head(teach.df) str(teach.df)

head(teach.df) 显示前六行数据，例如：

lang IQ method
1 72 87 1
2 75 119 1
3 85 121 1
4 70 112 1
5 73 100 1
6 86 133 1

str(teach.df) 显示数据框的信息，提示 method 原来是 integer 类型。

将 method 转换为因子：

teach.df$method <- factor(teach.df$method) print(teach.df$method) # 检查转化后的结果

显示因子变量的水平：Levels: 1 2 3。

绘制散点图（显示 IQ 与语言成绩的关系）：

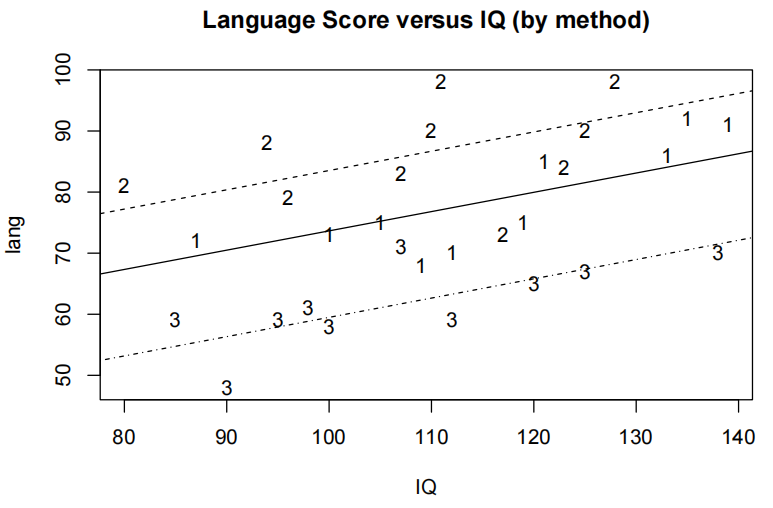
plot(lang ~ IQ, ylim = c(40, 110), pch = as.character(teach.df$method), ylab = "Language score", main = "Language Score versus IQ (by method)", data = teach.df)

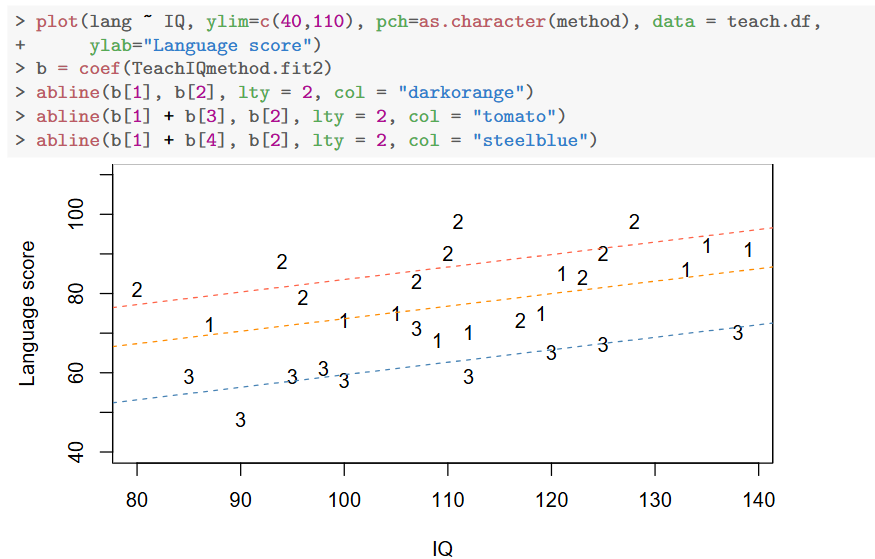
图中不同教学方法用不同字符（“1”、“2”、“3”）标识。教材中指出可以观察到三条大致平行的直线，表明各教学方法中 IQ 对语言成绩的斜率相似，但各组截距不同。

平行直线的出现提示我们无需引入交互项，即不必为每种教学方法计算不同的 IQ 斜率。

图形结果说明：

图中显示三条平行直线分别代表教学方法 1、2、3（分别由不同颜色和线型表示），直观反映出：

IQ 对成绩的正向斜率一致；

三方法间因截距不同而存在显著差异，这与模型输出完全一致。

模型拟合（含交互项）与诊断

拟合含交互项的模型：

TeachIQmethod.fit <- lm(lang ~ IQ * method, data = teach.df) summary(TeachIQmethod.fit)

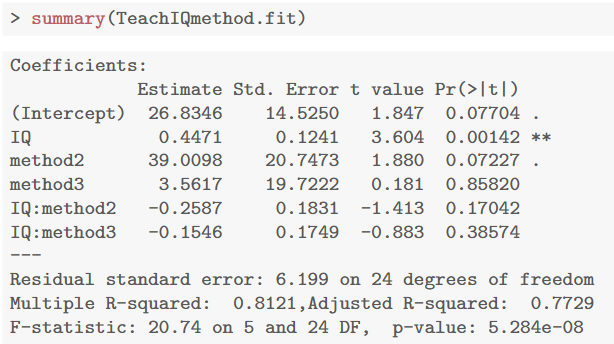
教材展示了 residuals vs fitted 的图、QQ图以及 Cook’s 距离图，均显示假设检查基本满足。

ANOVA 检验交互项：

anova(TeachIQmethod.fit)

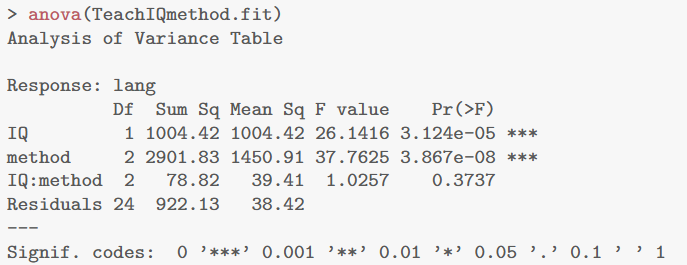
交互项（IQ:method）的 P 值为 0.3737，远大于显著性水平 0.05，说明交互项不显著，即 IQ 对语言成绩的影响不因教学方法而改变。

anova:验证交互项是否对模型产生影响。判断方法：就看交互项的p value是否大于0.05/小于0.05，大于就是拒绝没有影响的原假设，不考虑交互项；反之还是需要考虑交互项

拟合无交互（主效应）模型并解读结果

拟合无交互项模型：

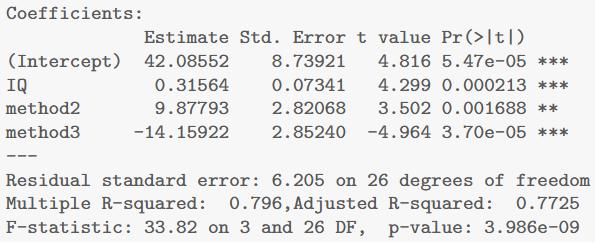
TeachIQmethod.fit2 <- lm(lang ~ IQ + method, data = teach.df) summary(TeachIQmethod.fit2)

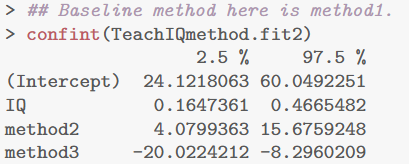
求置信区间：

confint(TeachIQmethod.fit2)

基于结果逐项解读

IQ 的效应：

IQ 的系数约为 0.31564，表示在相同教学方法下，每增加 1 个 IQ 点，语言成绩平均增加 0.316 分。
将其乘以 10 得到每增加 10 个 IQ 点，成绩大约增加 3.16 分；而置信区间 (0.16474, 0.46655) 乘以 10，则得到 (1.65, 4.67) 分，即“每增加 10 IQ 点成绩增加约 1.6 至 4.7 分”。

教学方法 2 的效应：

method2 的系数为 9.87793，说明在控制 IQ 后，教学方法 2 相对于方法 1 的学生，平均语言成绩高 9.88 分；其 95% 置信区间为 (4.08, 15.68)，说明这种差异在 4.1 至 15.7 分之间。

教学方法 3 的效应：

method3 的系数为 –14.15922，说明在相同 IQ 下，教学方法 3 的学生平均语言成绩比方法 1 低 14.16 分；其 95% 置信区间为 (–20.02, –8.30)，说明差异大约在 8.3 至 20 分之间（取绝对值理解）。

改变参考组比较（方法 2 与方法 3 直接对比）：

为了直接比较方法 3 与方法 2 的差异，我们将参考水平设为方法 2。

teach.df$method <- relevel(teach.df$method, ref = "2") TeachIQmethod.fit3 <- lm(lang ~ IQ + method, data = teach.df) summary(TeachIQmethod.fit3) confint(TeachIQmethod.fit3)

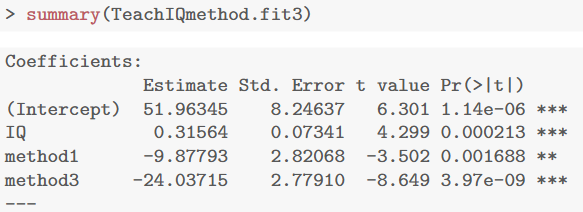
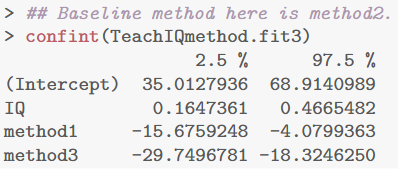
得到的方法3与方法2之间的差值为 –24.04 分，置信区间说明该差值大约在 18.3 到 29.7 分之间（负号表示方法 3 的成绩较低）。

分析思路总结

数据预处理与探索性分析：

检查数据结构，将数值标签转换为因子。

绘制散点图（或使用 trendscatter 函数）并观察是否能区分不同组的数据走势。

模型构建：

首先拟合含交互项的模型，观察交互项的显著性（例如通过 summary 和 anova 输出）。

如果交互项不显著，则采用无交互项的主效应模型（平行直线模型）。

结果输出与解读：

查看模型摘要中各变量的系数、标准误和 P 值。

使用 confint 获取 95% 置信区间，然后根据 IQ 系数乘以 10 得出“每增加 10 IQ 点”的效果；

对因子变量，直接比较虚拟变量系数的正负及置信区间，得出不同教学方法间的效果差异。

如有需要，通过 relevel 改变参考组获得直接的组间比较。

第九章R语言代码总结

1.更换分类变量的参考水平

R语言默认对于分类变量选择“1”作为参考水平，而有时候可能需要“2”作为参考水平。对应示例代码为

teach.df$method=relevel(teach.df$method,ref="2")

2.处理题目中需要判断是否采用交互项问题的大致流程

①首先还是正常按照乘法拟合模型

TeachIQmethod.fit=lm(lang~IQ*method,data=teach.df)

②然后正常EOV check流程要做

plot(TeachIQmethod.fit)

normcheck(TeachIQmethod.fit)

cooks20x(TeachIQmethod.fit)

③用anova判断是否提出交互项interaction

data.frame(anova(TeachIQmethod.fit))

④交互项不显著就重新拟合一个“加法”模型

TeachIQmethod.fit2=lm(lang~IQ+method,data=teach.df)

summary(TeachIQmethod.fit2)

注意：写lm时必须要把多因子放在后面，比如说有不同的method但是IQ只有一个，因此就写作lm(lang~IQ+method)而不能lm(lang~method+IQ)

[!s]

使用 anova 函数进行联合假设检验时，一定要注意模型中解释变量的排序问题。具体意思如下：

顺序效应（Sequential Sum of Squares）：
anova() 默认基于“顺序效应”（Type I Sum of Squares）来分解总变差，即按照模型中变量出现的顺序来计算每个变量增加的额外解释能力。如果某个多水平因子不是排在所有其他变量的最后面，那么它的检验结果（如F值和P值）会受到前面变量顺序的影响。

因子测试的位置：
为了检验一个多水平因子的联合假设（例如判断这个因子的所有虚拟变量系数是否都为零），这个因子应该出现在 anova 输出中“Residuals”上面那一行，也就是作为最后一个进入模型的解释变量。这样，其测试结果才是比较纯粹地反映该因子对模型的增量贡献，而不会受到前面变量已解释部分的干扰。

例子说明：
在教材中给出的例子中，原先模型中使用的是 lm(lang ~ IQ + method, data = teach.df)，而后改变了变量顺序为 lm(lang ~ method + IQ, data = teach.df)。两种模型下 anova 输出中各变量的 P 值确实发生了变化：

当 method 在 IQ 后面时，method 的 P 值反映的是在已包含 IQ 之后 method 能解释的额外变差。

当 method 在 IQ 前面时，method 的 P 值反映的是 method 第一次进入模型时所解释的变差，而 IQ 的测试则是在 method 已经进入模型之后的效果。

虽然在这个例子中改变顺序后，P 值有所不同，但最终对结论（例如哪些变量显著）没有影响；不过在其他情况下，因顺序不同可能会导致结论不同。

总之，在用 anova 来检验多水平因子时，为了确保检验结果准确，必须把这个因子放在模型公式的最后。这样能更好地测试这个因子整体是否有显著作用，否则变量出现的先后顺序可能会影响分解的平方和，导致 P 值的变化，从而可能改变检验结论。

Case Study 9.1: Language score vs teaching method and student IQ

Problem

教育专家对三种不同的教学方法中哪一种最能提高不同能力水平儿童的语言测试成绩感兴趣——这些能力水平是通过智商来衡量的。此外，他们还想知道这些方法的相对有效性是否因智商而异。

为此，进行了一项实验，将30名学生随机分配到三个组，每组采用不同的教学方法。这种随机化是为了确保每个组内都有不同能力水平的学生。由于学生们处于测试环境中，我们可以假设他们的测试成绩彼此独立。

感兴趣的变量是：

lang：学生的语言分数。

IQ：学生在教学计划开始前的智商。

method：对学生使用的教学方法类型。

Question of Interest

我们希望看到语言得分是否取决于教学方法。我们想要检查智商的任何混淆效应。

Read in and Inspect the Data

data(teach.df)

head(teach.df)

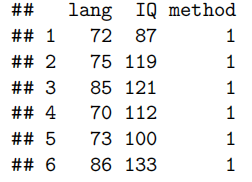
str(teach.df)

# 我们需要将方法转换为因素变量

teach.df$method=factor(teach.df$method)

plot(lang~IQ,main="Language Score versus IQ(by method)"

,pch=as.character(teach.df$method),data=teach.df)

从编码散点图中，我们可以看到三条平行线。看起来分数随着智商的提高而增加，方法2得分最高，方法3得分最低。这些单独散点图中出现的变异度要低得多。

Model Building and Check Assumptions

teach.fit=lm(lang~IQ*method,data=teach.df)

plot(teach.fit,which=1)

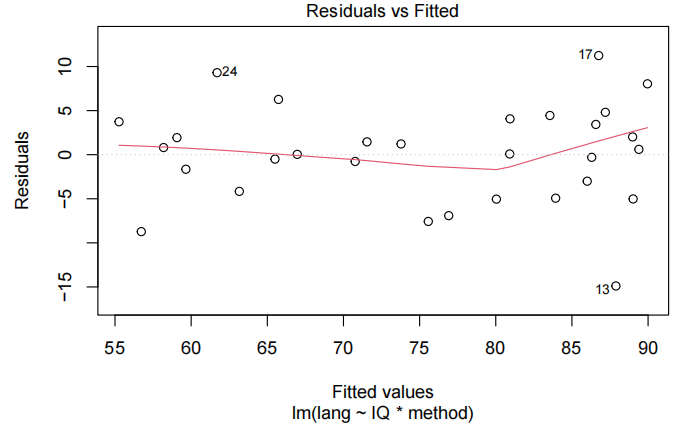
normcheck(teach.fit)

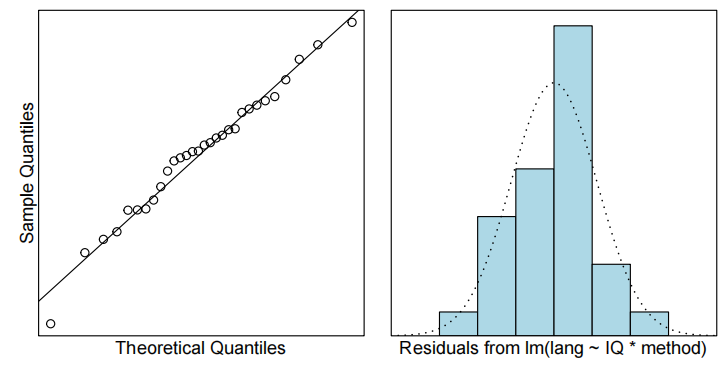
cooks20x(teach.fit)

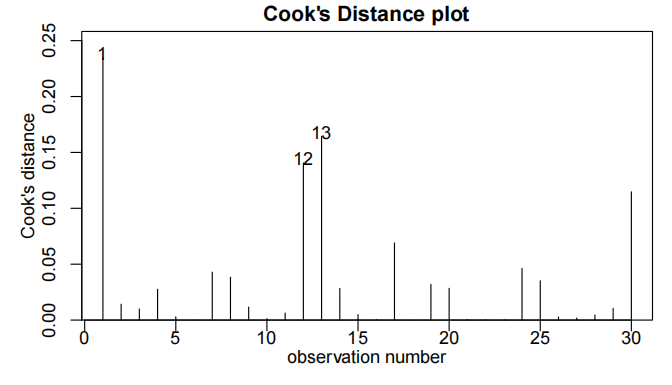
anova(teach.fit)

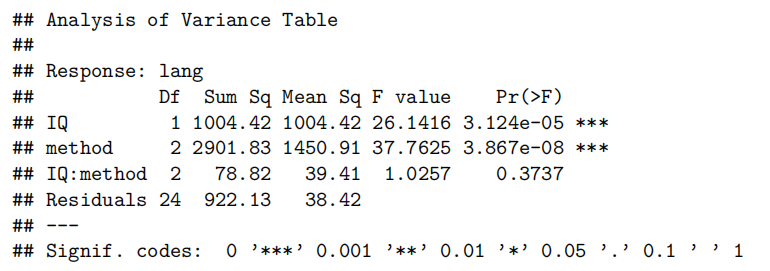
可以看到IQ:method项p value值已经大于0.05因此拒绝有影响的原假设

teach.fit2=lm(lang~IQ+method,data=teach.df)

plot(teach.fit2,which=1)

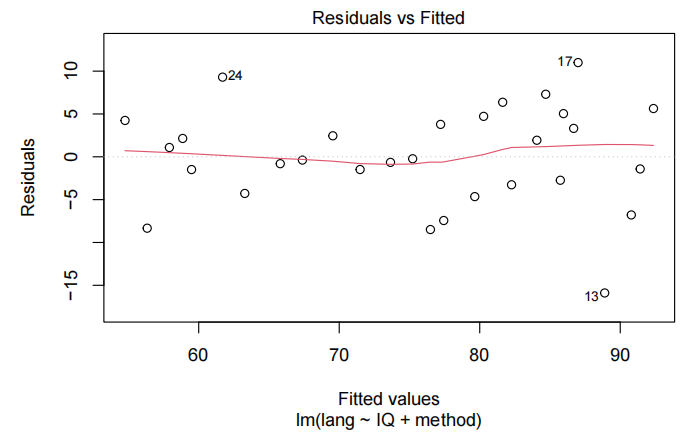
normcheck(teach.fit2)

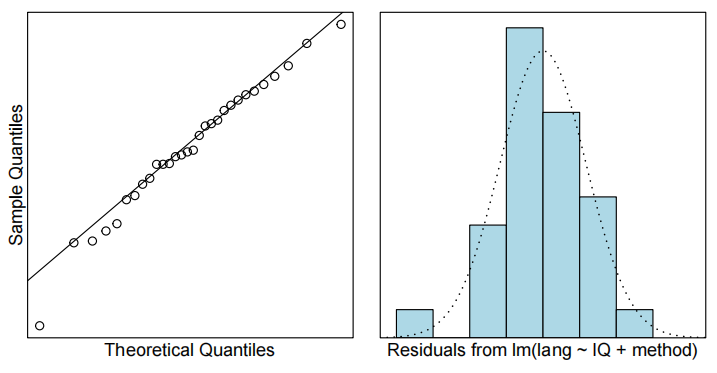
cooks20x(teach.fit2)

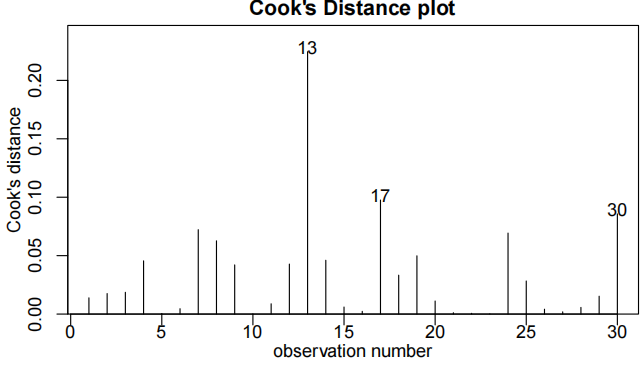
anova(teach.fit2)

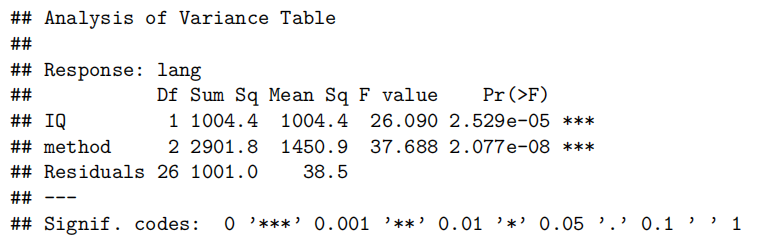
summary(teach.fit2)

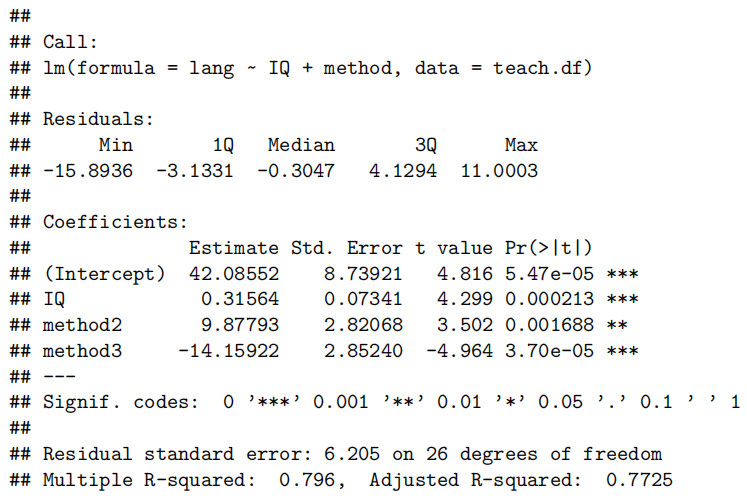
## F-statistic: 33.82 on 3 and 26 DF, p-value: 3.986e-09

confint(teach.fit2)

Visualise the Final Model

plot(lang~IQ,main="Language Score versus IQ(ny method)",

pch=as.character(teach.df$method),data=teach.df)

abline(teach.fit2$coef[1], teach.fit2$coef[2], lty = 1)

abline(teach.fit2$coef[1] + teach.fit2$coef[3], teach.fit2$coef[2], lty = 2)

abline(teach.fit2$coef[1] + teach.fit2$coef[4], teach.fit2$coef[2], lty = 4)

Generate Model Output for when method’s baseline is “2”

teach.df$method=relevel(teach.df$method,ref="2")

teach.fit3=lm(lang~IQ+method,data=teach.df)

confint(teach.fit3)

## 2.5 % 97.5 %

## (Intercept) 35.0127936 68.9140989

## IQ 0.1647361 0.4665482

## method1 -15.6759248 -4.0799363

## method3 -29.7496781 -18.3246250

Method and Assumption Checks

为了解释语言得分，我们首先使用教学方法、智商及其交互作用作为解释变量拟合模型。但是，交互项并不显著（P值= 0.37)。因此，我们重新拟合了去除交互项后的模型。

所有模型假设均得到满足。[可选：学生应独立行动，因为他们被随机分配到不同的教学方法中，并且在测试条件下进行测量。]

我们的最终模型是

$l a n g_{i} = β_{0} + β_{1} \times I Q_{1} + β_{2} \times m e t h o d . m e t h o d 2_{i} + β_{3} \times m e t h o d . m e t h o d 3_{i} + ε$

其中：

如果学生i采用方法2，则将method.method2i设为1，否则设为0；

如果学生i采用方法3，则将method.method3i设为1，否则设为0；

$ε_{i}$ ∼ $i i d N (0, σ^{2})$

这里方法1是我们的基线。

最终模型也使用方法2作为基线进行了重新拟合。注意：当我们改变基线（到第2级）时，虚拟变量的值会发生变化，使得method.method2i变为method.method1i。因此，如果学生i接受了方法1，则method.method1i设为1，否则为0。

我们的模型解释了语言分数变异的近80%。

Case Study 9.3: Water Hardness and Mortality

本案例研究的数据来源于对环境因素导致疾病的研究。数据显示了1958年至1964年间，英格兰和威尔士61个大城镇的男性每10万人年死亡率，以及这些城镇饮用水中的钙浓度（以百万分之一计）。（钙浓度越高，水越硬。）数据集中，至少位于德比以北的城镇被标记为N。在本研究中，我们将使用R软件探讨死亡率与水硬度之间的关系，以及这种关系是否受地理因素影响。数据文件位于Canvas平台上的water.csv。

water.df<-read.csv("WATER.csv")

head(water.df)

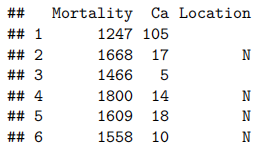
检查缺失值总是有用的。

sum(is.na(water.df))

## [1] 0

没有缺失值。一切正常。那来个图表怎么样？理想的图表应该用位置作为绘图符号，但我们看到南部的城镇被编码为空白。我们应该改变这一点。怎么做呢？如何将所有非N值设为S？

water.df$Location[water.df$Location != 'N'] = 'S'

## Warning in [<-.factor(tmp, water.df$Location != "N", value =

## structure(c(NA, : invalid factor level, NA generated

嗯，这并没有按计划进行。这是因为位置是一个因素。我们有几种选择：一是创建一个新的变量；二是将位置设置为字符向量，然后进行更改，最后再将其转换回因子。虽然这个选项听起来很复杂，但实际上只需要一行代码。这样做更优，因为这样可以避免工作空间中出现冗余信息。

water.df$Location = with(water.df, {

Location = as.character(Location);

Location[is.na(Location)] = 'S';

Location = factor(Location)

})

water.df$Location

## [1] S N S N N N N S N S S S N S S N N N N S N N N N N S N S N S S S N N S

## [36] S S N S N N N N N S S N N N N N S N S S S N N N S N

## Levels: N S

好多了。那图呢？

plot(Mortality~Ca, pch = as.character(water.df$Location), data = water.df)

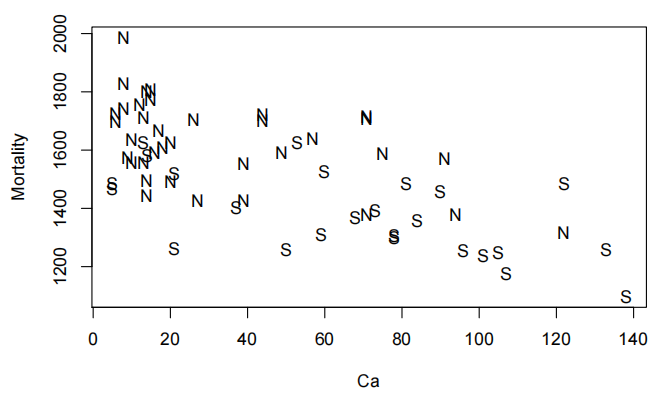
water.fit<-lm(Mortality~Ca*Location,data=water.df)

plot(water.fit,which=1)

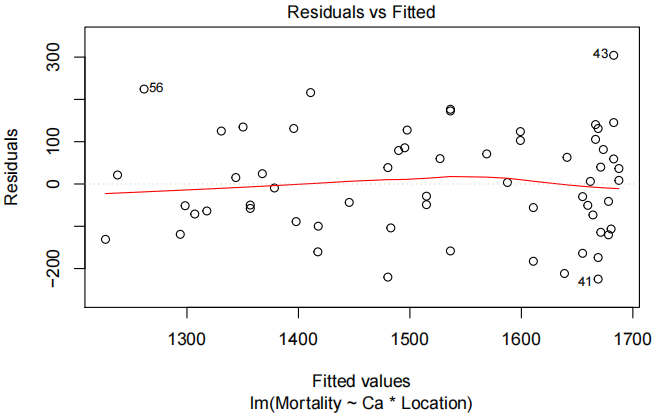
norncheck(water.fit)

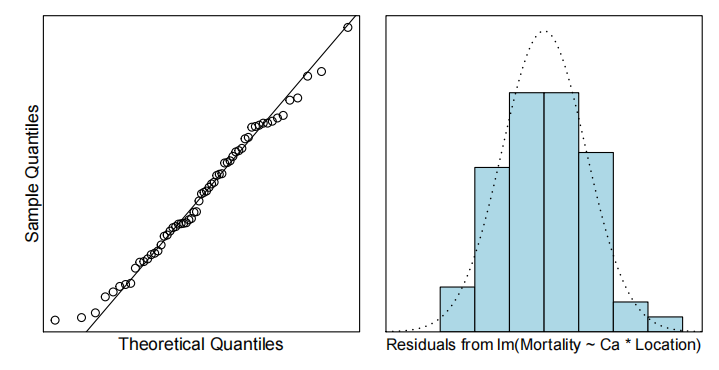
cooks20x(water.fit)

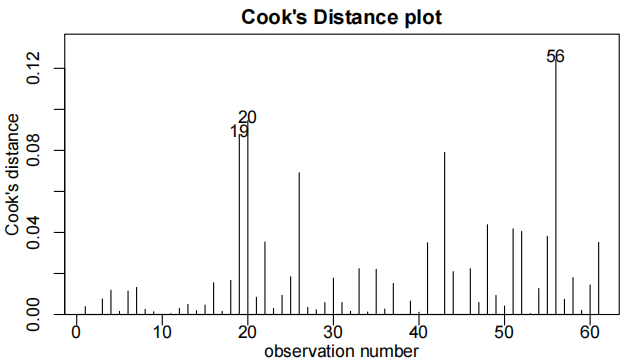
summary(water.fit)

##

## Call:

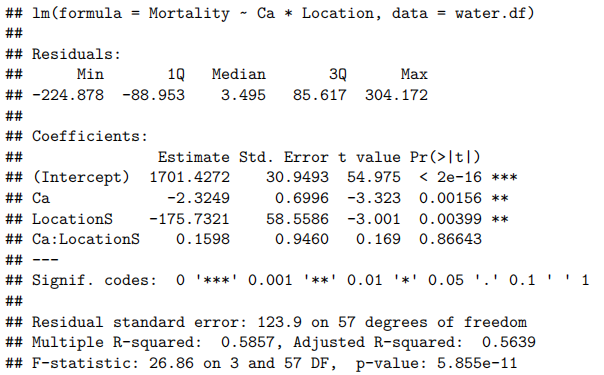
看起来没有证据显示斜率存在差异。我们能从ANOVA表中获得其他信息吗？

anova(water.fit)

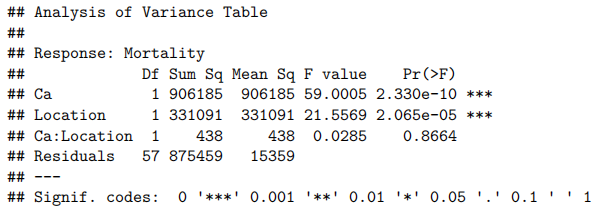
不。我们只有两个水平，因此不需要ANOVA表来进行此分析。

因此，我们没有观察到相互作用，但似乎硬度与之存在关联，并且似乎还存在南北方向效应（位置）。我们应当重新拟合模型。

water.fit2<-lm(Mortality~Ca+Location,data=water.df)

sumamry(water.fit2)

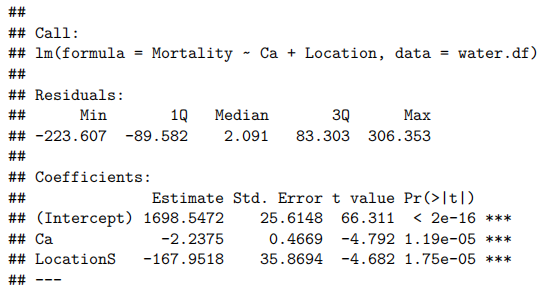
R²的变化极小。拟合线在图表上的表现如何？

b = coef(water.fit2)
plot(Mortality~Ca, pch = as.character(water.df$Location), data = water.df)
abline(b[1:2], col = "blue", lty = 2, lwd = 2)
abline(b[1] + b[3], b[2], col = "red", lty = 2, lwd = 2)
legend("topright", lty = 2, lwd = 2, col = c("blue", "red"),
legend = c("North", "South"), bty = "n")
# This code puts some confidence bounds around the lines.
# It's pretty complicated if you don't know R and it isn't examinable
pred.df = data.frame(Ca = rep(seq(0, 160, by = 20), 2),
Location = rep(c('N', 'S'), c(9, 9)))
water.pred = predict(water.fit, newdata = pred.df, interval = "confidence")
for(i in 1:2){
idx = 1:9 + (i - 1) * 9
for(j in c("lwr", "upr")){
lines(pred.df$Ca[idx], water.pred[idx, j], lty = 3, lwd = 2, col = "lightgrey");
} }

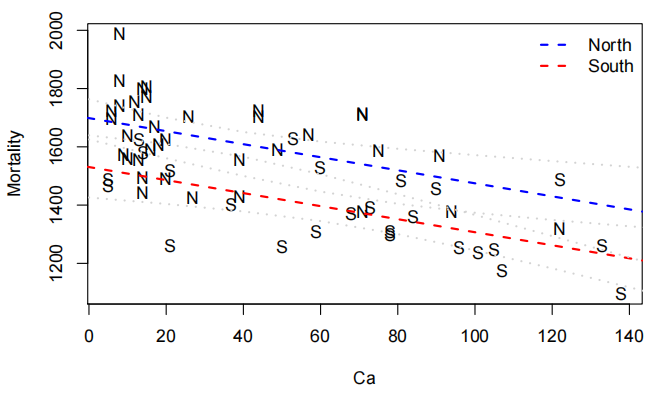
所以看起来随着水中钙浓度的增加死亡率就会降低，而且南方的死亡率比北方低。所以看起来随着水中钙浓度的增加死亡率就会降低，而且南方的死亡率比北方低。

Chapter 10: Multiple linear regression models（多元线性回归模型）

多元线性回归模型的本质与适用场景

模型定义

多元线性回归模型用于描述一个响应变量$ y $与多个解释变量 $x_{1}, x_{2}, \dots, x_{p}$ 的线性关系，形式为： $E [y] = β_{0} + β_{1} x_{1} + β_{2} x_{2} + \dots + β_{p} x_{p}$ 。通过最小二乘法估计参数 $β_{0}, β_{1}, \dots, β_{p}$ ，使残差平方和最小。模型可包含数值型变量（如孕期天数、母亲身高）和分类型变量（如吸烟状态、是否头一胎），通过虚拟变量处理分类型变量。

核心思想

多变量影响分析：同时考察多个解释变量对响应变量的影响，控制其他变量后分析单个变量的边际效应。
效应叠加性：假设各解释变量对 y 的影响是线性可加的，适用于探索复杂关系（如孕期天数对出生体重的分段效应）。
模型扩展：可通过交互项（如$ x_1 \times x_2$）或非线性变换（如二次项、分段函数）处理变量间的非线性或交互作用（如例题中通过 “逾期天数” 构建分段斜率模型）。

参数解释与推断

截距项$ \beta_0$：所有解释变量为 0 时响应变量的期望值（需结合实际变量定义域解释，避免无意义外推）。
斜率项 $β_{j}$ ：控制其他变量后， $x_{j}$ 每增加 1 单位，y 的平均变化量（对分类型变量，如吸烟状态， $β_{j}$ 表示两类间的均值差异）。
假设检验
- 单个变量：通过 t 检验判断 $β_{j}$ 是否显著不为 0（p < 0.05）。
- 整体模型：通过 F 检验判断所有解释变量是否联合显著，或使用 $R^{2}$ 、调整 $R^{2}$ 评估模型拟合优度（如例题中最终模型 $R^{2} = 30.5 %$ ，表示解释变量解释了 30.5% 的出生体重变异）。

数据特征与模型假设

数据特征
- 需探索变量间的两两关系（如散点图、相关系数矩阵），识别线性趋势、异常值或共线性（如母亲体重与 BMI 高度相关）。
- 分类型变量需转换为虚拟变量（如 “是否头胎” 用 0/1 表示）。
模型假设
- 线性关系：响应变量与解释变量的关系在参数上是线性的（可通过残差图检验）。
- 独立性：观测值之间相互独立（适用于随机样本数据）。
- 正态性与等方差：残差服从均值为 0 的正态分布且方差齐性（通过normcheck(model)和残差图检验）。
- 无多重共线性：解释变量之间无强线性相关（通过方差膨胀因子 VIF 或相关系数矩阵识别，如例题中 BMI 与体重高度相关导致参数估计不稳定）。

例题：婴儿出生体重的多元线性回归分析

问题

探索孕期天数、母亲特征（年龄、身高、体重、BMI）、吸烟状态及是否头胎对婴儿出生体重的影响，构建最优预测模型。

数据

响应变量：出生体重（bwt，盎司）。
解释变量
- 数值型：孕期天数（gestation）、母亲年龄（age）、身高（height）、体重（weight）、BMI（由体重和身高计算）。
- 分类型：是否头胎（not.first.born，0 = 头胎，1 = 非头胎）、吸烟状态（smokes，0 = 不吸烟，1 = 吸烟）。
数据来源：1174 条观测，来自伯克利统计实验室数据集。

数据探索与预处理

变量关系可视化

使用pairs20x()绘制散点图矩阵（课本分开绘制了连续变量和非连续变量的pairs20x，原因会在下面解释），发现

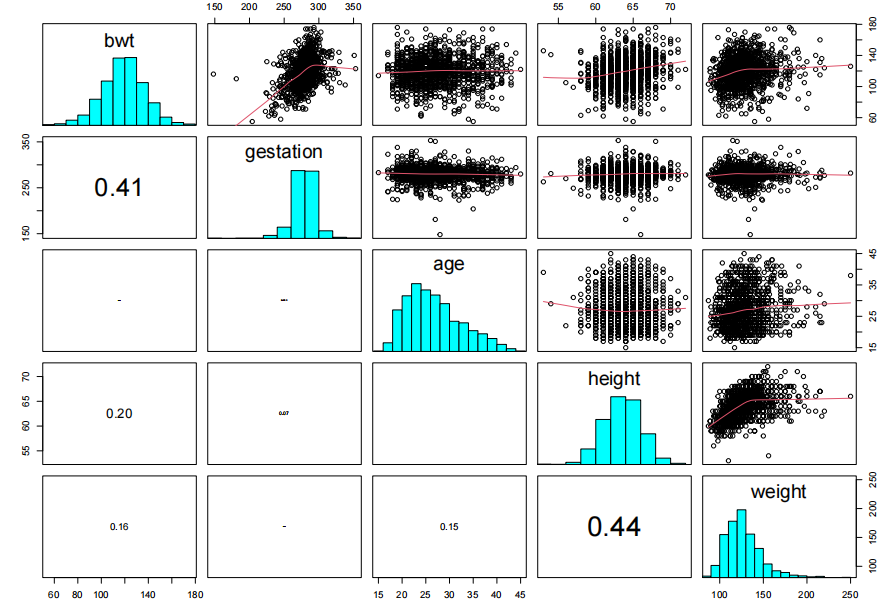
孕期天数（gestation）与出生体重呈 “曲棍球棒” 型关系（294 天前正相关，294 天后增速放缓）。

母亲身高、体重与出生体重弱正相关，年龄无明显关联。（图片依次展示出生体重与身高、体重和年龄的关系）

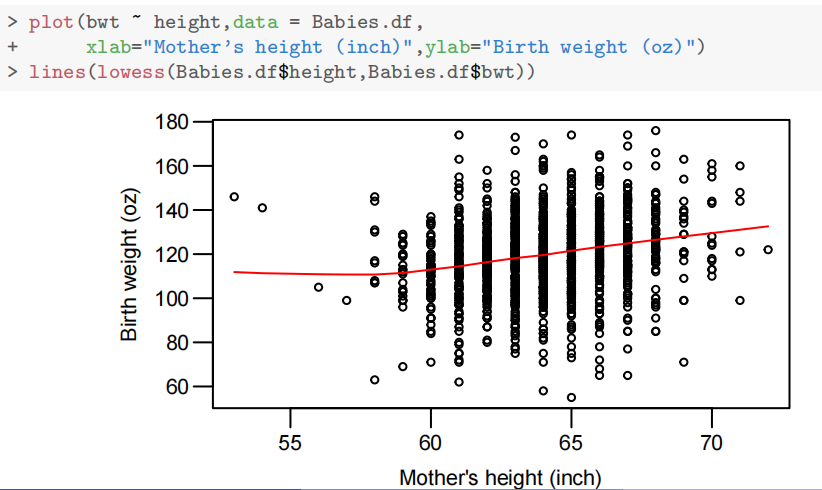
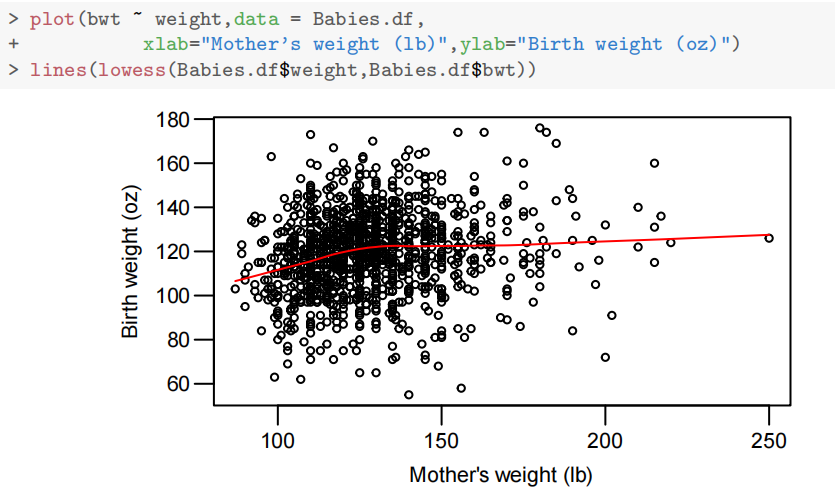
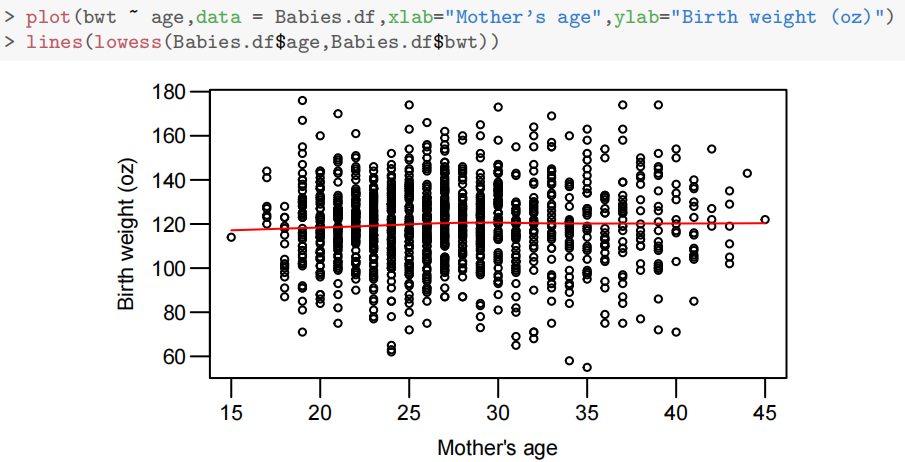
image-20250422153752941age

吸烟母亲的婴儿体重略低，是否头胎影响不显著（初步分析）。

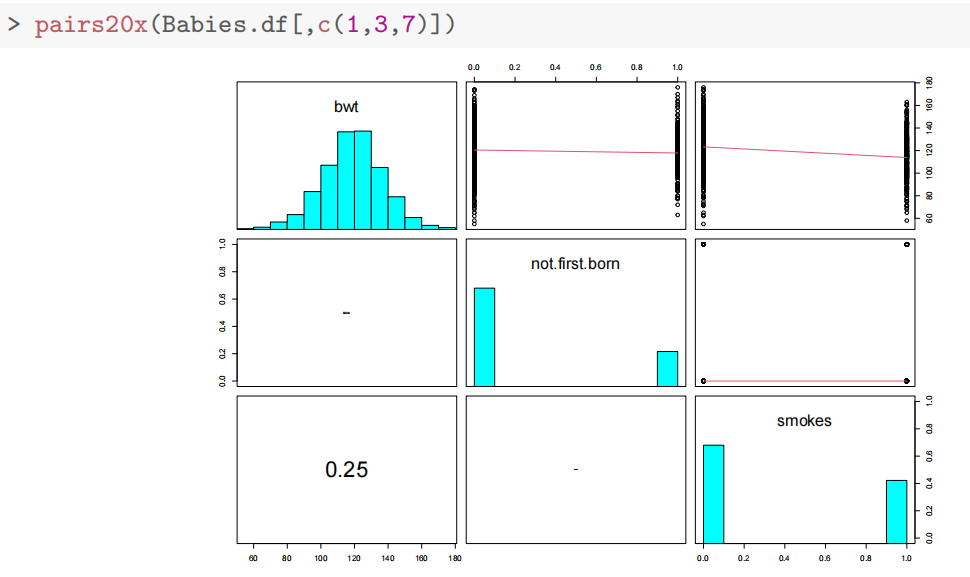
异常值处理
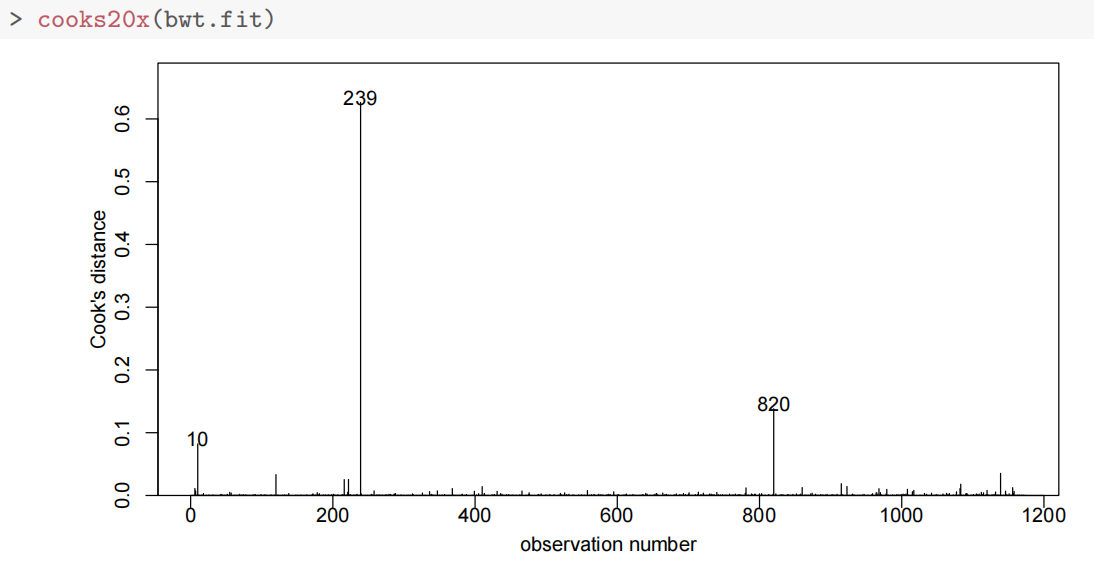
- 识别并删除孕期小于 200 天的异常观测（如观测 239 和 820，可能为数据录入错误），避免对模型产生过度影响（通过cooks20x(model)检测高 Cook 距离点）。

第239个数据点影响过大，这个婴儿的胎龄只有148天，但体重却和足月婴儿一样。这显然是一个数据录入错误，我们将删除这个数据点。

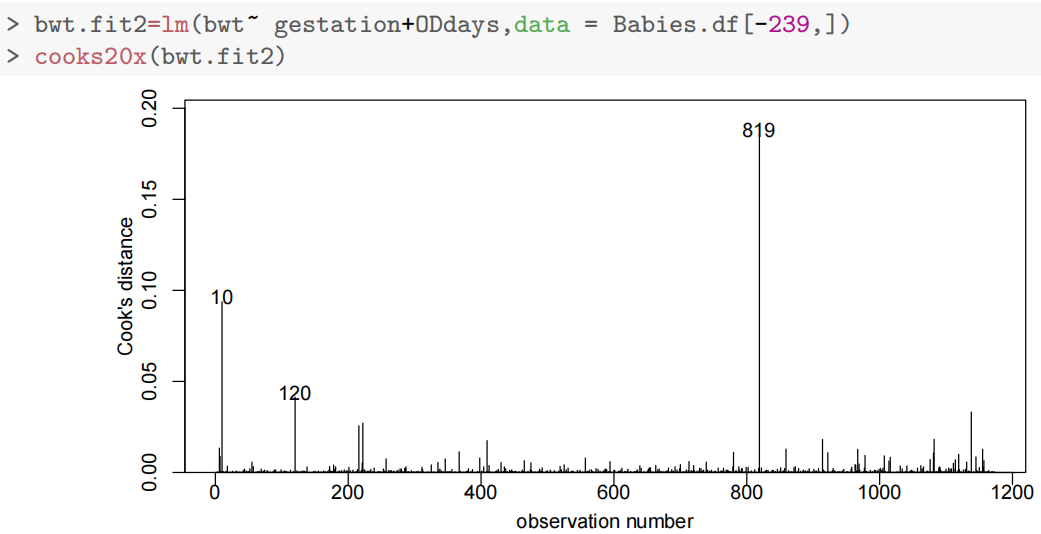
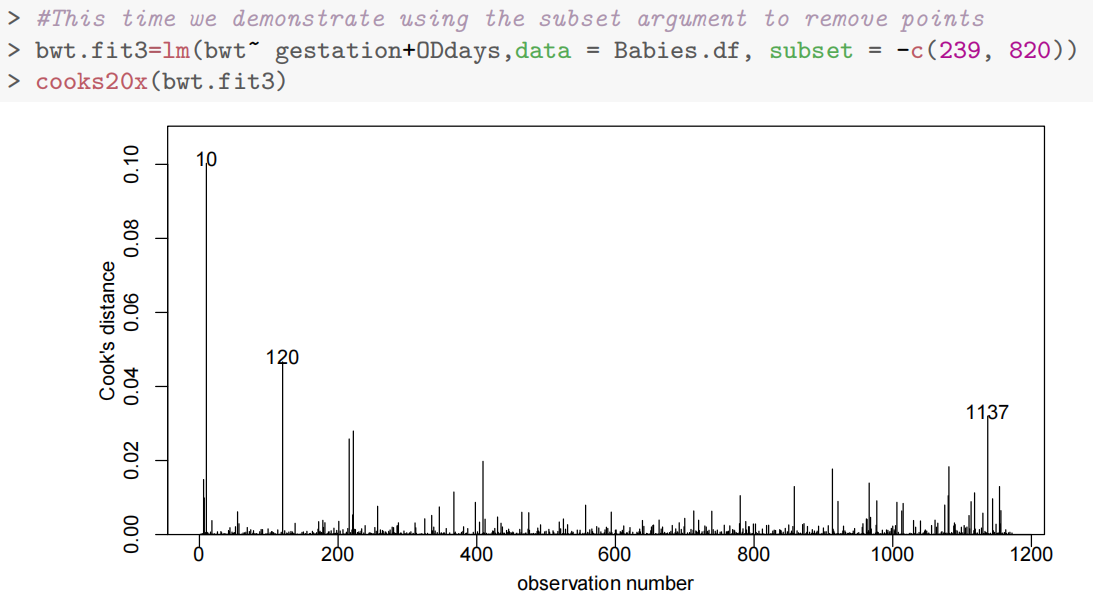
尽管观察结果820（因为删掉了239后原来的820就变成819了，因此下文代码还是用的820，因为是和239同时删除的）没有过度影响，我们还是做出判断，将其删除。

模型构建与调整

分段线性模型（孕期效应）
- 定义 “逾期天数” $O D d a y s = m a x (g e s t a t i o n - 294, 0)$ ，构建分段斜率模型： $E [b w t] = β_{0} + β_{1} gestation + β_{2} ODdays$ 其中，孕期≤294 天时，斜率为 $β_{1}$ ；孕期 > 294 天时，斜率为 $β_{1} + β_{2}$ （实际拟合结果显示逾期后斜率为负，即体重增长停滞）。

逐步添加变量与多重共线性处理

添加身高：显著提升模型拟合度（ $R^{2}$ 从 21.9% 升至 24.6%），参数显著（ $p < 2 e - 16$ ）。

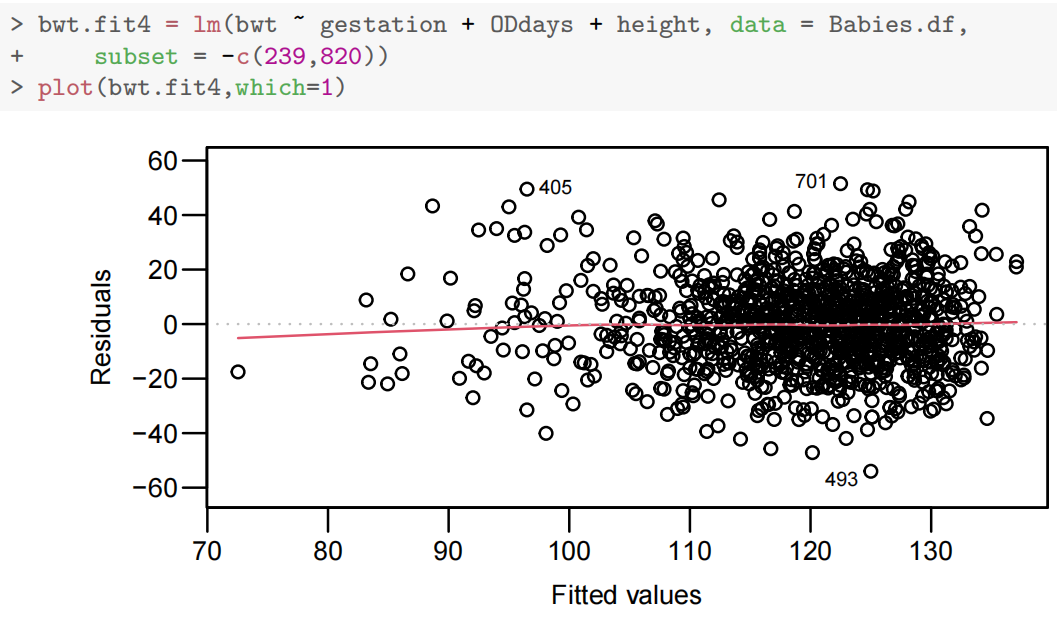
添加体重：进一步提升拟合度，但与身高存在相关性（相关系数 0.44）。

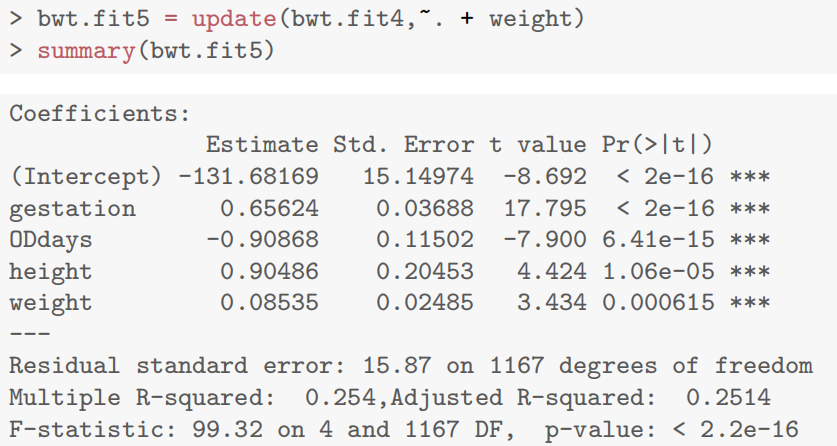
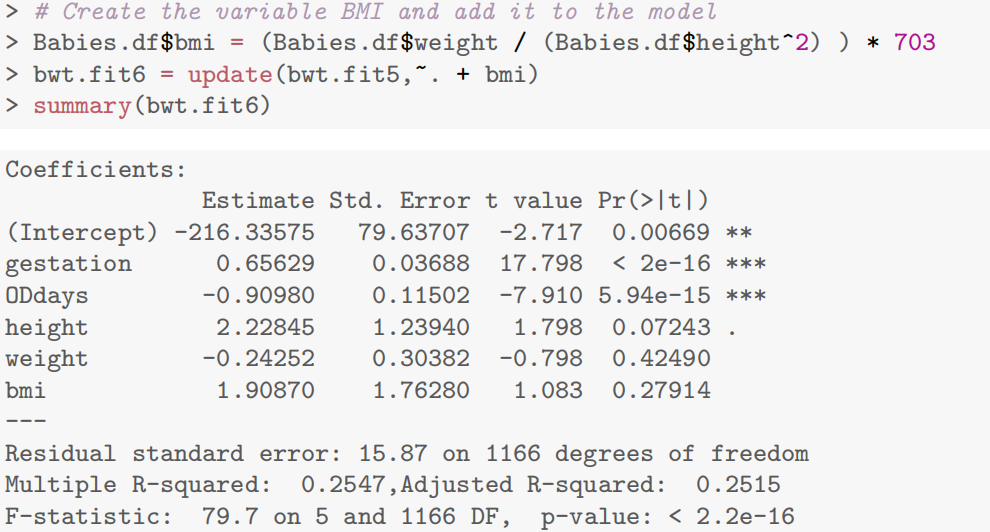
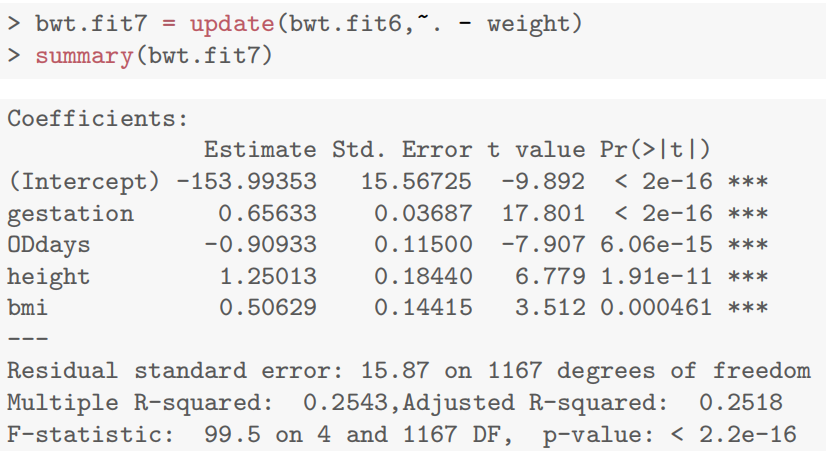
添加 BMI：因 BMI 由体重和身高计算，导致严重多重共线性（体重、身高、BMI 的参数显著性消失），最终剔除体重，保留 BMI 或身高之一（如模型 bwt.fit7 剔除体重后，BMI 参数显著）。

分类型变量纳入

吸烟状态（smokes）纳入后，参数显著为负（ $p = 0.00315$ ），表明吸烟母亲的婴儿体重平均降低约 7.94 盎司。

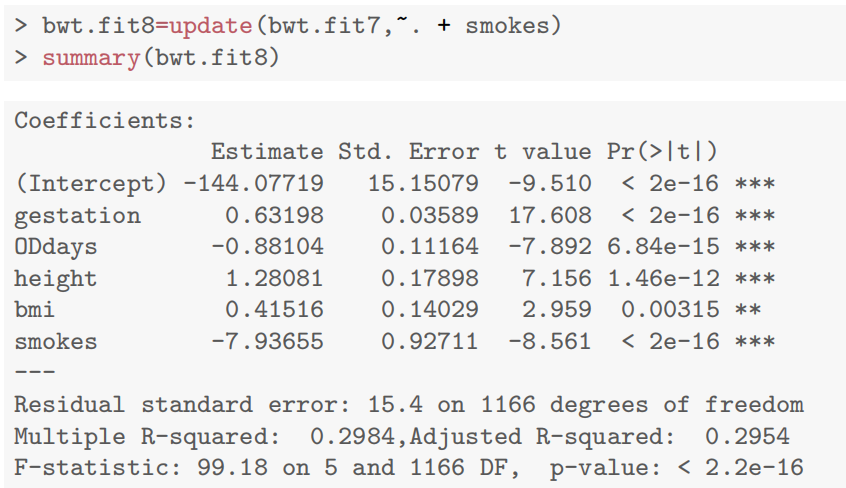
是否头胎（not.first.born）纳入后，参数显著为负（ $p = 0.000672$ ），但需结合实际背景解释（可能受家庭规模变化影响）。

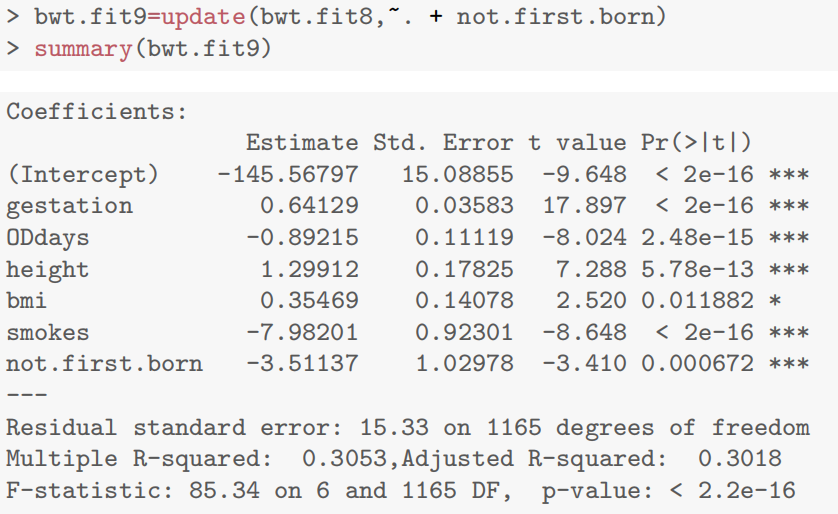
第十章R语言代码总结

1.检查不同变量的线性关系

注意：要将连续变量和非连续变量（0-1变量）分开分析，否则会混乱

pairs20x(Babies.df[,c(1,2,4,5,6)])

pairs20x(Babies.df[,c(1,3,7)])

2.基于原有模型更新新自变量/减少原有自变量

model2=update(model1,~.± $x_{v a r i b l e 2}$ )

问题解答

1.怎么看pairs20x画出来的图

（1）对角线元素

每个对角线位置（如第一行第一列的 sl、第二行第二列的 sx 等）展示单个变量的直方图，用于观察变量的分布形态（如是否对称、偏态方向等）。例如：

sl 的直方图显示其数值分布情况，可判断数据集中趋势与离散程度。

（2）非对角线元素

散点图与拟合线：非对角线格子展示两个变量的散点图，红色曲线（或直线）为拟合线，用于初步判断变量间是否存在线性或非线性关系。例如：

第一行第三列（sl 与 rk）的散点图若呈现明显上升趋势，结合旁边的相关系数 0.87（强正相关），说明二者线性关系显著。

相关系数：部分格子中标注的数字（如 0.87、0.23 等）是对应两个变量的皮尔逊相关系数，取值范围 [-1, 1]，绝对值越大，线性相关性越强。例如：

sl 与 rk 的 0.87 表示强正相关；sx 与 rk 的 0.23 表示弱正相关。

（3）变量间关系综合分析

观察散点图的点分布密度与趋势：若点沿拟合线密集分布，变量间关系较明确；若点分布分散，则关系较弱。

结合相关系数与散点图：如 yr（第四行第四列直方图）与其他变量的散点图，可分析 yr 与 sl、rk 等的关联强弱及方向。

2.为什么要分开绘制连续变量和非连续变量的pairs20x

| 数据类型 | 可视化方法 | 分析目标 | 避免的问题 |
| --------------- | ------------------------ | ----------------------------- | -------------------------- |
| 连续变量 | 散点图、直方图、相关系数 | 探索线性 / 非线性关系、共线性 | 分类变量散点图无意义 |
| 分类 + 连续变量 | 箱线图、分组对比 | 组别差异检验、显著性判断 | 错误使用相关系数、图形混乱 |

数据类型的差异导致可视化目标和方法不同

连续变量（如孕期天数、母亲身高、体重）：

取值为连续区间内的任意值，变量间关系适合用散点图展示趋势（如线性、非线性），用相关系数量化关联强度，对角线位置用直方图或核密度图展示单变量分布。

例：孕期天数（gestation）与出生体重（bwt）的散点图可直观呈现 “曲棍球棒” 型曲线关系。

非连续变量（分类变量）（如是否头胎、吸烟状态）：

取值为有限个离散类别（如 0/1），与连续变量的关系更适合用箱线图或分组均值对比展示类别间差异，而非散点图（因分类变量无 “顺序” 或 “距离” 概念）。

例：吸烟状态（smokes）与出生体重的关系，通过箱线图可清晰对比吸烟组与非吸烟组的体重分布差异。

可视化目标的差异

避免图形混淆与信息过载

混合绘制的问题:若将连续变量与分类变量强行放入同一 pairs 图

分类变量的散点图无意义（如 “是否头胎” 只有 0/1 两个值，散点图会压缩在两条竖线上，无法展示趋势）。

对角线的直方图对分类变量不适用（分类变量应展示频数分布而非连续密度）。

相关系数对分类变量失效（分类变量与连续变量的关联需用 t 检验或 ANOVA，而非 Pearson 相关）。

分开绘制的优势:聚焦数据类型，让图形更 “适配” 分析目标，避免视觉干扰。

连续变量图中，可通过lowess平滑曲线发现非线性趋势（如孕期天数超过 294 天后体重增长停滞）。

分类变量图中，箱线图直接展示组间中位数差异（如吸烟母亲的婴儿体重更低）。

2.如何判断update变量是否有价值？——看update后的summary看 $R^{2}$ 的变化情况，增加了通常就是好的。但是在此过程中要考虑多重共线性问题。

3.如何理解多重共线性multi-collinearity /ˌmʌlti kəˌlɪnɪˈærɪti/

多重共线性指多元回归中，两个或多个解释变量之间存在强线性相关关系（如母亲体重与 BMI 高度相关）。

（1）表现形式

非独立信息：变量间高度相关，导致模型无法区分各自对响应变量的影响。

参数估计不稳定：系数的标准误增大，t 检验显著性降低（如课本中 BMI 与体重共存时参数显著性消失）。

（2）实际影响

模型难以解释：无法准确衡量单个变量的边际效应。

假设检验失效：可能误判变量重要性（如本应显著的变量因共线变得不显著）。

4.为什么pairs20x(Babies.df[,c(1,2,4,5,6)])的df,前面是空的

逗号前后分别对应行索引和列索引。

row_indices（行索引）：若留空（即逗号前无内容），表示选取 所有行（等价于 1:nrow(dataframe)）。

column_indices（列索引）：通过 c(1,2,4,5,6) 指定选取第 1、2、4、5、6 列。

在 pairs20x(Babies.df[,c(1,2,4,5,6)]) 中，数据框前的空（即 [, 中的行索引为空）是 R 语言选取数据框子集的语法规则，若留空（即逗号前无内容），表示选取 所有行（等价于 1:nrow(dataframe)）。

Case Study 10.1: Birthweight of babies

Background

让我们来考察影响婴儿出生体重的因素。

出生体重：以盎司为单位

孕期：以天数表示

not.first.born：0=首次分娩，1=非首次分娩

年龄：母亲的年龄，以岁为单位

身高：母亲的身高，以英寸为单位

出生前体重：母亲的孕前体重，以磅为单位

吸烟：母亲的吸烟状况，0=不吸烟，1=吸烟。

该数据集来自http://www.stat.berkeley.edu/users/statlabs/labs.html.，附于德博拉·诺兰和特里·斯皮德合著的优秀教材《统计实验室：通过应用学习数理统计》（施普林格-弗拉格出版社，2001年）。

Question of Interest

我们想建立一个模型来解释婴儿的出生体重。

Read in and Inspect the Data

Babies.df=read.table("babies_data.txt",header=T)

piars20x(Babies.df[,c(1,2,4,5,6)])

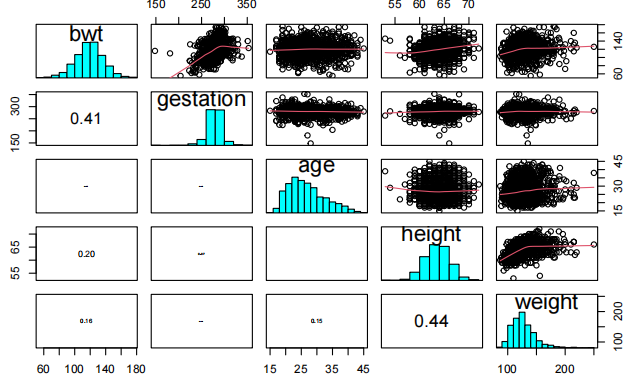
查看配对图，我们发现婴儿体重与母亲身高和体重之间存在较弱的关系。

然而，婴儿的胎龄（妊娠期）与其体重之间存在更强的关系，这并不令人意外，因为孩子在母亲子宫内的时间越长，获得营养和成长的时间就越长——但也有个限度——之后这种关系会趋于平缓。

母亲年龄与孩子体重之间似乎没有关系。

让我们更深入地探讨婴儿体重与胎龄之间的关系。

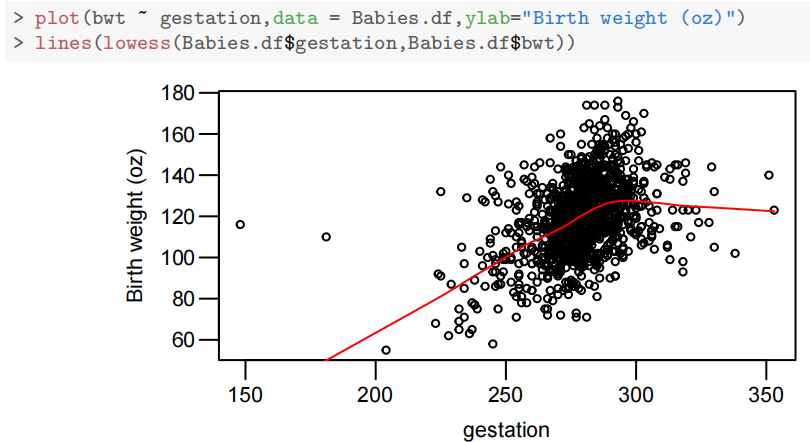
plot(bwt~gestation,data=Babies.df,col="gray60")

lines(lowess(Babies.df$gestation,Babies.df$bwt),col="tomato",lwd=2)

text(152,120,"?")

text(185,115,”?”)

abline(v=294,col="steelblue",lwd=2)

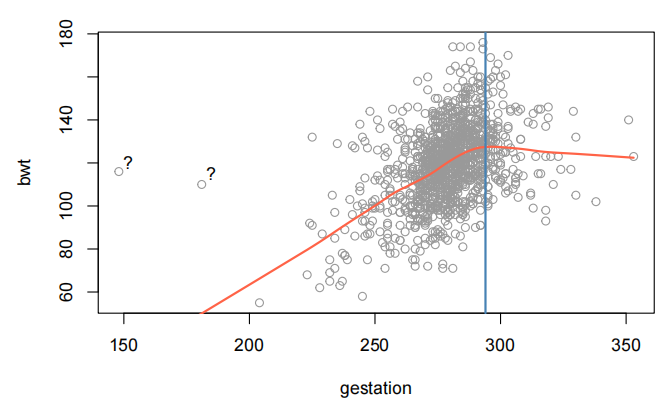
请注意，这些图表中似乎有一些“奇怪”的数据点。X轴之间的关系并不明显。也就是说，解释变量之间似乎没有很强的关系。

大多数婴儿在42周= 42∗7 = 294天前出生（美国妇产科医师学会-孕期宝宝如何成长”。参见https://www.acog.org/-/media/For-Patients/faq156.pdf?dmc=1&ts=20150329T2112264959.）。超过这个时间点后，婴儿似乎停止生长，因此出现了“平坦化”和/或减少。我们将为此时间点创建一个虚拟变量OD（逾期）。

让我们看看分类（因子）数据变量与婴儿出生体重（bwt）的关系。

它们是not.first.born和吸烟。

pairs20x(Babies.df[,c(1,3,7)])

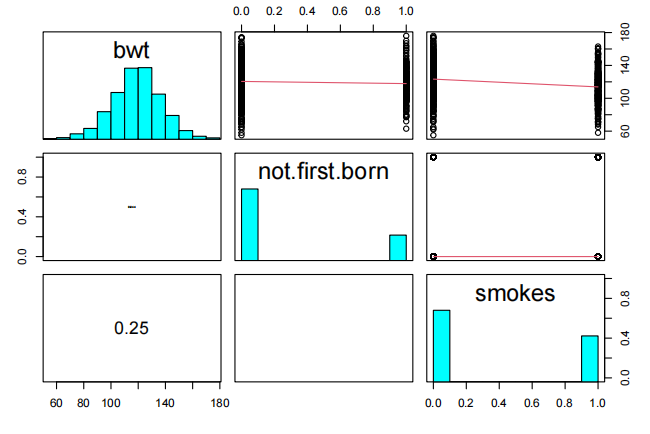
在这里，我们只看到母亲吸烟（吸烟）与婴儿出生体重之间存在轻微的关系。如果母亲吸烟，婴儿的出生体重会略有下降。这增加了母亲吸烟导致低出生体重婴儿的风险——也许这是避免烟草的另一个理由！

变量not.first.born似乎没有太大的影响——考虑到家庭规模在发达国家显著减少（这是美国的数据），这一变量可能不再像以前那么重要，这也许并不令人意外。我们稍后会再检查这一点。

Model Building and Check Assumptions

#让我们创建OD（虚拟变量），如前面所述。

Babies.df$OD=1*(Babies.df$gestation>294)

range(Babies.df$gestation[Babies.df$OD==0]) #Check

## [1] 148 294

range(Babies.df$gestation[Babies.df$OD==1]) #Check

## [1] 295 353

bwt.fit=lm(bwt~gestation*OD,data=Babies.df)

eovcheck(bwt.fit)

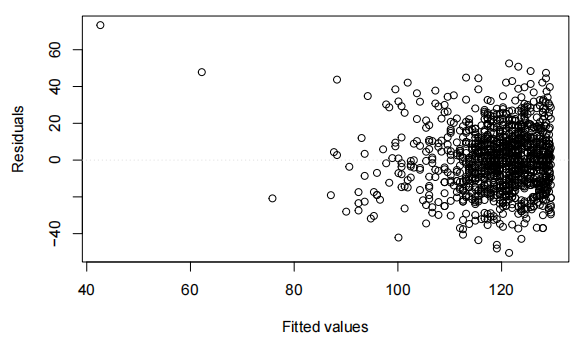
cooks20x(bwt.fit)

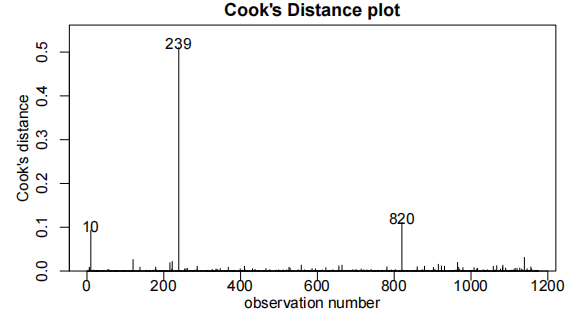
bwt.fit2=lm(bwt~gestation*OD,data=Babies.df[-239,])

cooks20x(bwt.fit2)

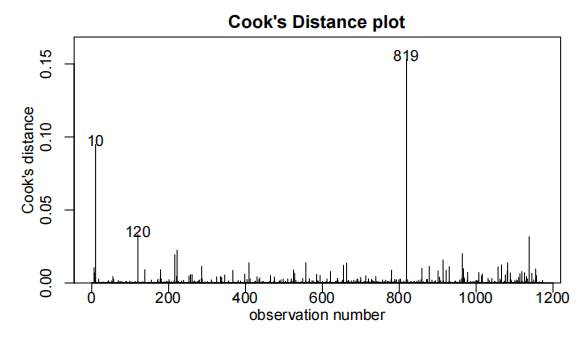
bwt.fit3=lm(bwt~gestation*OD,data=Babies.df[-c(239,820),])

cooks20x(bwt.fit3)

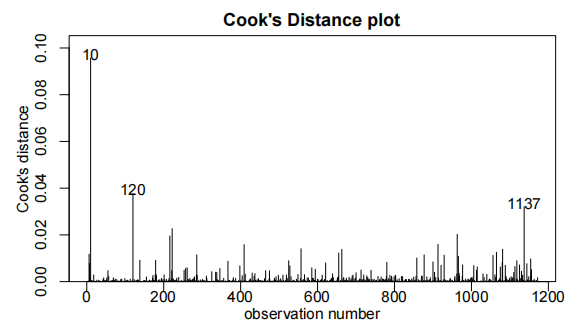
bwt.fit4=lm(bwt~gestation*OD+weight,data=Babies.df[-c(239,820),])

summary(bwt.fit4)

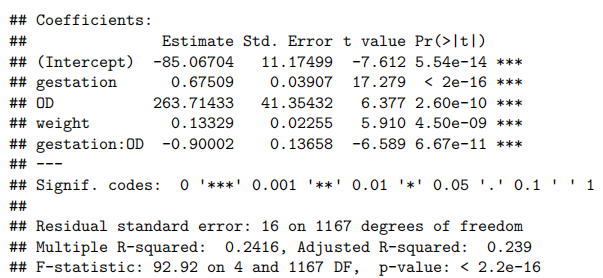
bwt.fit5<-lm(bwt~gestation*OD+weight+height,data=Babies.df[-c(239,280),])

summary(bwt.fit5)

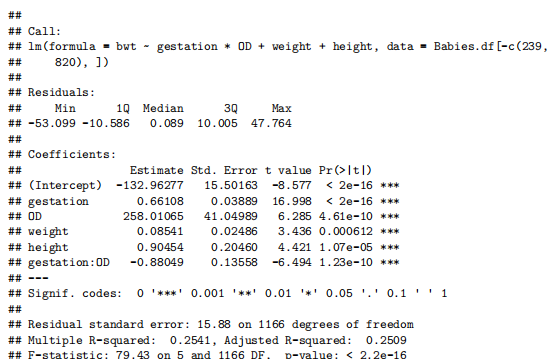
#让我们从这两个测量值中创建BMI

Babies.df$bmi=with(Babies.df,weight/(height^2)*703)

bwt.fit6=lm(bwt~gestation*OD+weight+height+bmi,data=Babies.df[-c(239,820),])

summary(bwt.fit6)

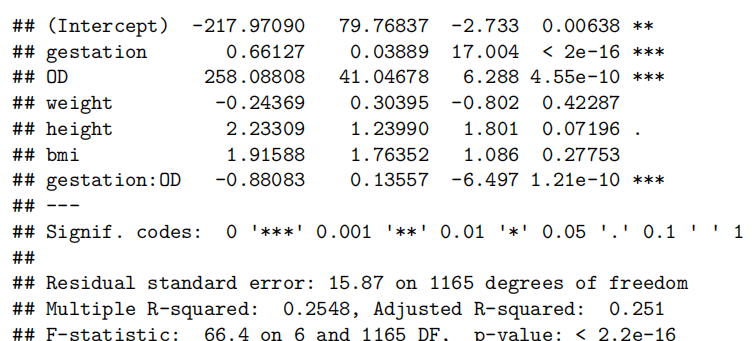
bwt.fit7=lm(bwt~gestation*OD+height+bmi+not.first.born,data=Babies.df[-c(239,820),])

summary(bwt.fit7)

bwt.fit8=lm(bwt~gestation*OD+height+bmi+not.first.born+smokes,data=Babies.df[-c(239,820),])

summary(bwt.fit8)

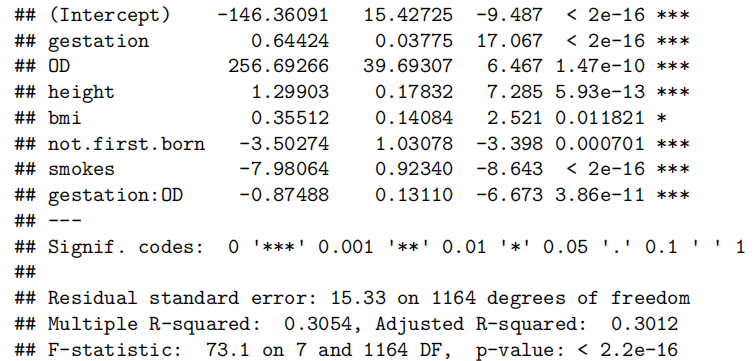
cooks20x(bwt.fit8)

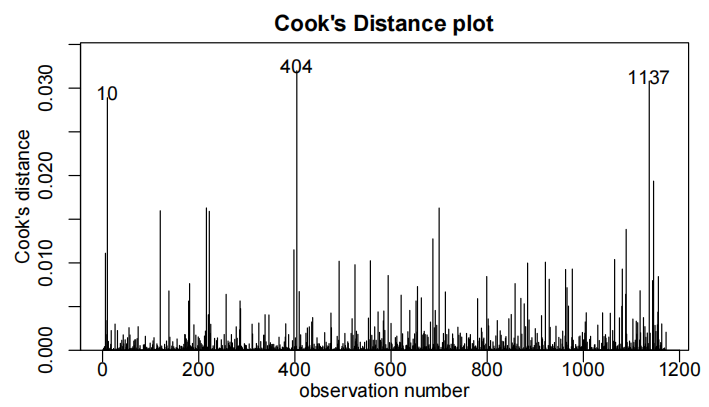
normcheck(bwt.fit8)

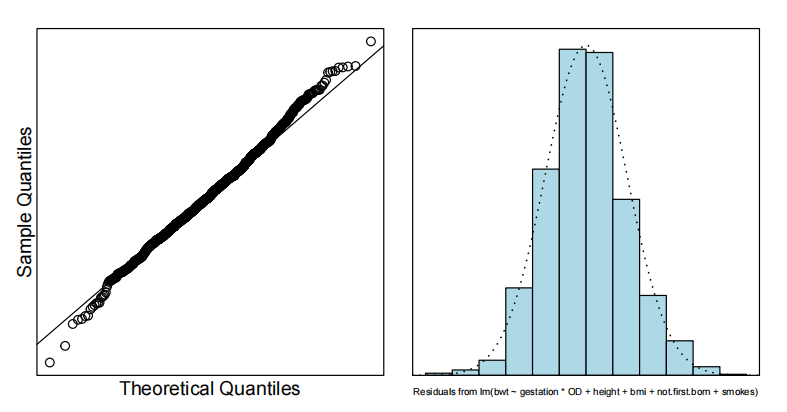
confint(bwt.fit8)

Method and Assumption Checks

查看配对图，我们发现出生体重与多个解释变量有关。我们将构建一个多元线性回归模型，并选择合适的解释变量。

观察值239和820被发现具有高度影响（highly influential）。它们被认为是异常值，因此从数据集中移除。

由于胎龄与出生体重之间的“曲棍球杆”关系需要根据婴儿是否过期来调整年龄效应，因此通过引入年龄与过期状态之间的交互项（interaction term）进行了拟合。此外，我们还决定将体重作为解释变量（explanatory variable）纳入（include）模型，但由于多重共线性（multi collinearity）不得不移除体重作为解释变量。最终模型满足所有假设条件。

使用前向模型选择法（即依次添加最有前景的解释变量），我们的最终模型是

$b w t_{i} = β_{0} + β_{1} \times g e s t a t i o n_{i} + β_{2} \times O D_{i} + β_{3} \times h e i g h t_{i} + β_{4} \times b m i_{i}$

$+ β_{5} \times n o t . f i r s t . b o r n_{i} + β_{6} \times s m o k e s_{i} + β_{7} \times g e s t a t i o n_{i} \times O D_{i} + ε_{i}$

其中i是独立同分布的 $ε_{i}$ ~ $i i d N (0, σ^{2})$ 分布，我们的三个指示变量（indicator variables）分别表示婴儿是否过期、是否不是第一个出生以及母亲是否吸烟。

我们的模型只能解释婴儿出生体重变化的31%。

Executive Summary

我们想建立一个模型来解释婴儿的出生体重。

在保持所有其他变量不变的情况下：

胎儿的预期出生体重随着孕期延长而增加——最多可达42周——之后，其体型会随着未出生时间的延长而逐渐减小。我们估计每增加一天孕期，出生体重平均增加0.57到0.71盎司。42周后，这一数值将减少约-0.61到-1.13盎司每增加一天孕期[注：如果我们改变OD基线可能会更好]。

我们估计母亲身高每增加一英寸，婴儿的出生体重平均增加0.94到1.64盎司。

我们估计母亲BMI每变化一个单位，婴儿的出生体重平均增加0.08到0.63盎司。

如果母亲吸烟，这会使婴儿的出生体重平均减少6.17到9.79盎司。

非独生子女似乎会使婴儿的出生体重平均减少1.48到5.52盎司。

Case Study 10.2: Gender difffferences in salary

Problem

这些是魏斯伯格的书中使用的工资数据，包括对一所小学院的52名教授的6个变量的观察。我们想要建立一个模型来预测工资。特别感兴趣的是性别对工资的影响（如果有）

关注的变量为：

sx：性别（女或男）

rk：职级（助理、副教授或正教授）

yr：在现任职级的年数

dg：最高学位（硕士或博士）

yd：获得最高学位后的年数

sl：学年工资，美元。

Question of Interest

我们想建立一个模型来解释工资。特别是，性别对工资的影响（如果有）

Read in and Inspect the Data

salary.df = read.table("salary.txt", header = T)

salary.df$sx=factor(salary.df$sx)

salary.df$dg=factor(salary.df$dg)

salary.df$rk=factor(salary.df$rk)

head(salary.df)

## sx rk yr dg yd sl

## 1 male full 25 doctorate 35 36350

## 2 male full 13 doctorate 22 35350

## 3 male full 10 doctorate 23 28200

## 4 female full 7 doctorate 27 26775

## 5 male full 19 masters 30 33696

## 6 male full 16 doctorate 21 28516

tail(salary.df)

## sx rk yr dg yd sl

## 47 female assistant 2 doctorate 6 16150

## 48 female assistant 2 doctorate 2 15350

## 49 male assistant 1 doctorate 1 16244

## 50 female assistant 1 doctorate 1 16686

## 51 female assistant 1 doctorate 1 15000

## 52 female assistant 0 doctorate 2 20300

paies20x(salary.df[,c("sl","sx","rk","yr","dg","yd")])

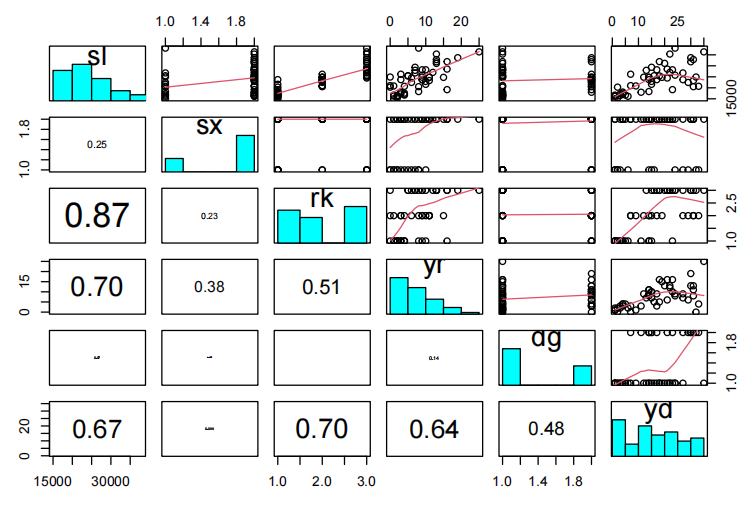
似乎男性比女性具有更高的平均斜率。等级越高，斜率越大（请注意，rk的水平按字母顺序排列）。随着yr的增加，预期的斜率也随之增加。斜率与直径之间的关系并不复杂。斜率与直径之间存在微弱的正相关关系。此外，随着直径的增加，斜率的变化也增大。

由于响应变量是薪资，因此使用对数薪资是合理的，这样效应将是乘法的。一些先前的分析也使用了对数（年）和对数（年份）作为解释变量。虽然这是否是最好的选择并不明显，但为了保持一致性，我们将遵循这些先前的分析。

salary.df$log.yr = log(salary.df$yr+1) *# log(yr + 1) since log(0) = -infinity

salary.df$log.yd = log(salary.df$yd)

salary.df$log.sl= log(salary.df$sl)

pairs20x(salary.df[, c("log.sl", "sx", "rk", "log.yr", "dg", "log.yd")])

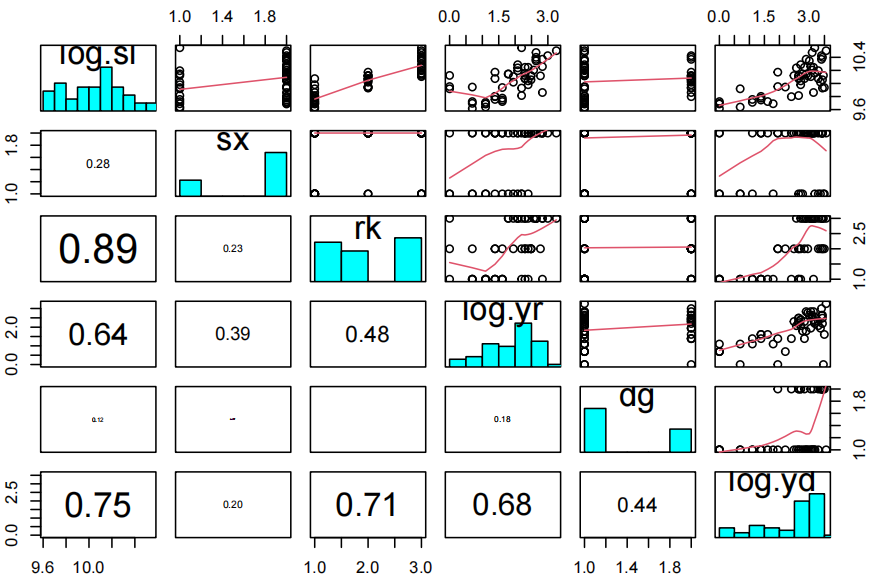
似乎男性比女性具有更大的平均对数（sl）。等级越高，对数（sl）也越高。随着对数（yr）的增加，预期的对数（sl）也随之增加。然而，较低的对数（sl）并不遵循这一观察趋势。对数（sl）与对数（dg）之间的关系并不复杂。对数（sl）与对数（yd）之间存在微弱的正相关关系。此外，随着对数（yd）的增加，对数（sl）的变化幅度也在增大。与对数（sl）和对数（yd）相比，情况有所改善。

我们将通过拟合所有项找到我们首选的模型，然后依次删除最不重要的项，直到所有剩余项都具有显著性。

Model Building and Check Assumptions

salary.fit=lm(log.sl~sx+rk+log.yr+dg+log.yd,data=salary.df)

plot(salary.fit,which=1)

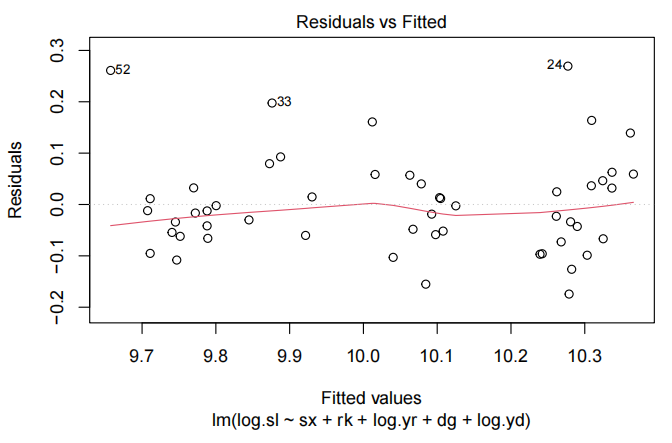
summary(salary.fit)

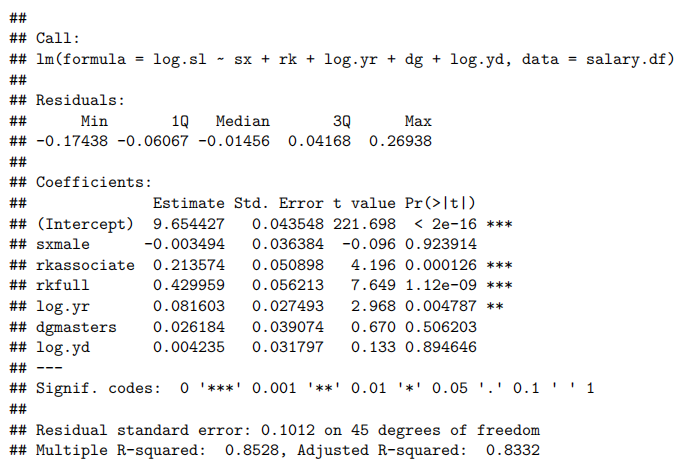
## F-statistic: 43.46 on 6 and 45 DF, p-value: < 2.2e-16

salary.fit2 = lm(log.sl ~ rk + log.yr + dg + log.yd, data = salary.df)

summary(salary.fit2)

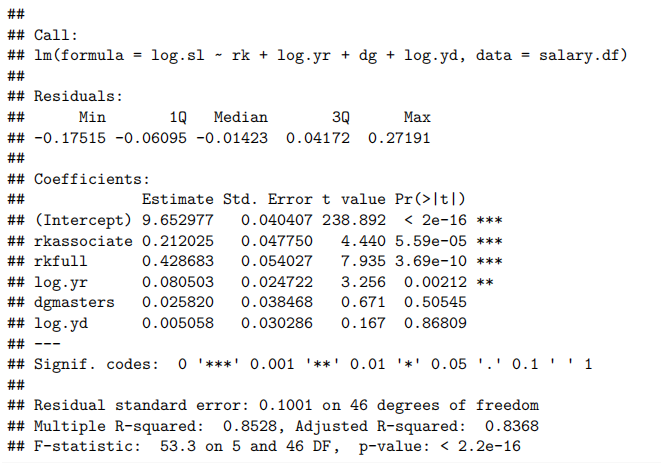
salary.fit3 = lm(log.sl ~ rk + log.yr + dg, data = salary.df)

summary(salary.fit3)

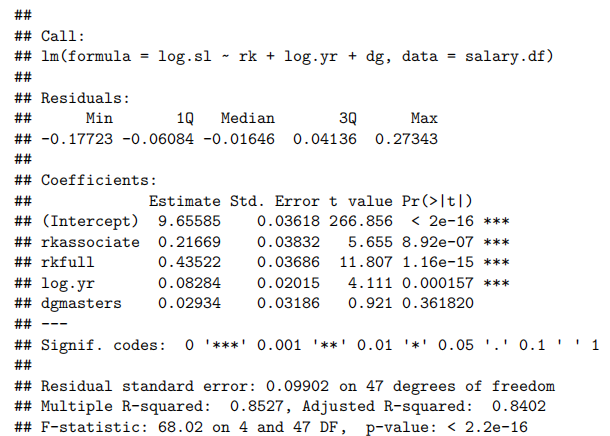
salary.fit4 = lm(log.sl ~ rk + log.yr, data = salary.df)

summary(salary.fit4)

##

## Call:

## lm(formula = log.sl ~ rk + log.yr, data = salary.df)

##

## Residuals:

## Min 1Q Median 3Q Max

## -0.15389 -0.06344 -0.02122 0.03568 0.26648

##

## Coefficients:

## Estimate Std. Error t value Pr(>|t|)

## (Intercept) 9.65710 0.03610 267.503 < 2e-16 ***

## rkassociate 0.22719 0.03653 6.220 1.16e-07 ***

## rkfull 0.43264 0.03670 11.789 8.85e-16 ***

## log.yr 0.08661 0.01970 4.396 6.08e-05 ***

## ---

## Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

## Residual standard error: 0.09886 on 48 degrees of freedom

## Multiple R-squared: 0.85, Adjusted R-squared: 0.8407

## F-statistic: 90.7 on 3 and 48 DF, p-value: < 2.2e-16

plot(salary.fit4,which=1)

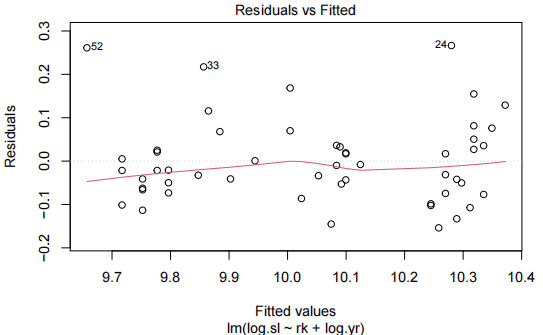
normcheck(salary.fit4)

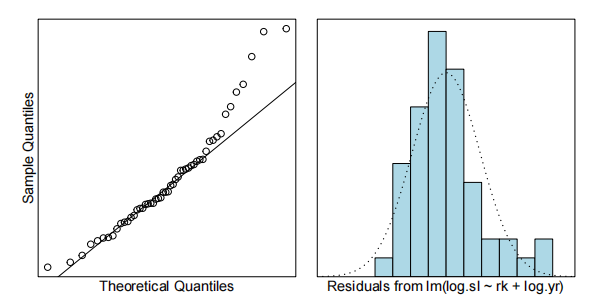
cooks20x(salary.fit4)

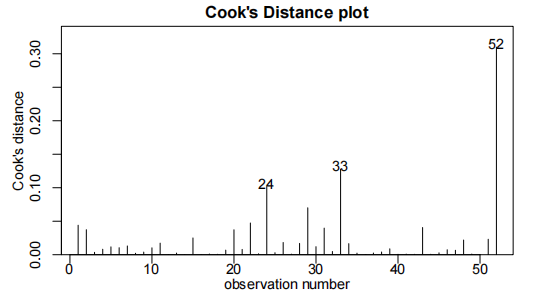
exp(confint(salary.fit4))

## 2.5 % 97.5 %

## (Intercept) 14537.893426 16809.266030

## rkassociate 1.166196 1.350709

## rkfull 1.431690 1.659352

## log.yr 1.048118 1.134534

Get log.yr Effffect for Doubling of Time at Current Rrank

2ˆconfint(salary.fit4)[4, ]

## 2.5 % 97.5 %

## 1.033112 1.091432

Method and Assumption Checks

我们有一个数值响应变量和多个解释变量，因此拟合了一个多元线性回归模型。在查看了成对图后，工资和两个年度的解释变量被取对数。

在拟合所有解释项后，应用奥卡姆剃刀原则去除了那些不显著的变量。我们按照以下顺序删除了这些变量：

• sx (P-value = 0.92).

• log(yd) (P-value = 0.87).

• dg (P-value = 0.36).

所有模型假设看起来都相当符合，尽管（notwithstanding）残差有点右偏（right skewed）。我们的最终模型是

$l o g (s a l a r y_{i}) = β_{0} + β_{1} \times r a n k a s s o c i a t e_{i} + β_{2} \times r a n k . f u l l_{i} + β_{3} \times l o g (y r_{i}) + ε_{i}$

其中 $ε_{i}$ ∼ $i i d N (0, σ^{2})$ 。这里rank.associate和rank.full分别等于1，如果rank是关联的或完全的，否则它们为零。

我们的模型解释了工资对数变异性的约85%。

Executive Summary

我们希望构建一个模型来解释薪资。特别是性别对薪资的影响（如果有的话）。

最终模型使用了教授的职称和当前职称的年数来解释其薪资。在调整了这些因素后，性别、最高学位以及获得最高学位以来的年数不再需要考虑。

我们估计，从助理教授晋升为副教授会使中位数工资增加17%到35%。

我们估计，从助理教授晋升为正教授会使中位数薪资增加43%到66%。

我们估计，在当前职级下，第三年薪资翻倍会使中位数薪资增加3.3%到9.1%。

在我们的模型变量中调整这些因素后，性别效应并不显著，但关于为何女性在高级学术职位中的比例如此之低，可能需要进一步探讨——可以认为需要做更多的工作来确定“性别差距”的原因。2这是逆向选择的一个例子——参见统计学330。

Chapter 11: Linear models with a single factor explanatory variable having three or more levels (One-way analysis of variance)具有三个或更多水平的单因素解释变量的线性模型（单因素方差分析）

模型定义

单因素方差分析（One-way ANOVA）用于分析一个具有 3 个或更多水平的因子变量 对连续响应变量的影响，本质是 多组均值差异检验 的线性模型。模型通过 指示变量（虚拟变量） 表示因子水平，形式为：

$y = β_{0} + β_{1} D_{2} + β_{2} D_{3} + . . . + β_{k - 1} D_{k} + ε$

$D_{i}$ 为第 i 组的指示变量（取值 0 或 1，基线组为 $D_{1} = 0$ ，
$β_{0}$ 为基线组均值， $β_{i}$ 为第 i 组与基线组的均值差异，
$ϵ \sim N (0, σ^{2})$ ，满足独立同分布正态假设。

核心思想

多组均值比较：通过 ANOVA 检验因子变量各水平的均值是否存在整体差异（F 检验），若显著则进一步进行 多重 pairwise 比较。
多重比较问题：直接进行多组两两 t 检验会增加第一类错误率（如 5 组有 10 次比较，未调整时整体错误率可达 40%），需通过 Tukey 调整 控制整体误差率（如 95% 同时置信区间）。

参数解释与推断

1. 参数含义

截距项 $β_{0}$ ：基线组（如 G1）的响应变量均值。
斜率项 $β_{i}$ ：第 i 组与基线组的均值差异：如$ G2 组均值 = \beta_0 + \beta_1$。

2. 假设检验

整体显著性（F 检验）：通过 ANOVA 表判断因子变量是否显著影响响应变量，检验统计量$ F = \frac{\text{组间均方 } } {\text{残差均方 } } $，对应$ p < 0.05$时拒绝原假设（存在至少一组均值不同）。
多重比较：使用 emmeans 包进行 Tukey 调整，计算所有两两比较的置信区间和校正 p 值，确保整体错误率≤5%。

数据特征与模型假设

1. 数据特征

因子变量：多水平分类变量（如 5 组果蝇处理方式：G1~G5），每组包含独立样本（如每组 25 只果蝇）。
响应变量：连续变量（如果蝇寿命天数），需通过箱线图初步观察组间差异（如 G5 组寿命显著低于其他组）。

2. 模型假设

线性关系：通过残差图（plot(model, which=1)）检验残差与拟合值无明显趋势。
独立性：样本独立（实验设计中各组独立随机分配）。
正态性与等方差
- 正态性：通过 Q-Q 图（normcheck(model)）或 Shapiro-Wilk 检验，残差近似正态分布。
- 方差齐性：残差图中各水平残差波动范围相近，或通过 Levene 检验。
无强影响点：通过 Cook 距离（cooks20x(model)）检测异常值，确保单个数据点不显著影响模型。

例题：果蝇寿命与繁殖活动的关系

1. 研究目标

分析 5 种处理组（G1：独居；G2：1 只感兴趣雌性；G3：8 只感兴趣雌性；G4：1 只不感兴趣雌性；G5：8 只不感兴趣雌性）对雄性果蝇寿命的影响。

2. 数据探索

箱线图：G5 组寿命显著低于其他组，G1、G2、G3、G4 组差异不明显。箱线图：G5 组寿命显著低于其他组，G1、G2、G3、G4 组差异不明显。

模型拟合：

Fruitfly.fit=lm(days~group,data=Fruitfly.df)

anova(Fruitfly.fit) #F=13.61,p=3.516e-09,显著拒绝原假设

多重比较：

使用 Tukey 调整后，G5 组与所有其他组均有显著差异（如 G1 vs G5：平均寿命差 24.84 天，95% CI [18.6, 31.1]），而其他组间无显著差异。

3. 结论

模型解释 31% 的寿命变异，G5 组（多只不感兴趣雌性）导致雄性果蝇寿命显著缩短，可能与 “性挫败” 相关。

第十一章R语言代码总结

1.使用箱线图检查因子的每个水平的数据

boxplot(days~group,data=Fruitfly.df)

2.R语言会自动指示基线，使用relevel函数可以改变baseline

Fruitfly.df$nwegroup=relevel(Fruitfly.df$group,ref="G2")

3.使用anova查看多变量均值的差异

anova(Fruitfly.fit)

4.通过Tukey调整多个成对比较的置信区间，以获取同时置信区间（CIs）

Fruitfly.pairs=pairs(emeans(Fruitfly.fit,~group,infer=T))

Case Study 11.1: Fruit-flies, sex and frustration

Problem

在这项研究中，我们研究了雄性果蝇的寿命与生殖活动之间的关系。（数据来自http://www.cvgs.k12.va.us:81/digstats/Imain.html）

如何定义果蝇的“兴趣”？以下是这项研究的定义：新受精的雌性通常在至少两天内不会再次交配。

所以，不感兴趣的雄性总是与新交配的雌性生活在一起！

假设是，独自生活或与不感兴趣的雌性生活的雄性会比与感兴趣的雌性生活的雄性活得更久。由于有多个组平均值，使用单因素方差分析来确定各组平均值之间是否存在显著差异。

研究设计将雄性果蝇分为以下几组：

1)独自生活的雄性

2)与一个感兴趣的雌性生活在一起的雄性

3)与八个感兴趣的雌性生活在一起的雄性

4)与一个不感兴趣的雌性生活在一起的雄性

5)与八个不感兴趣的雌性生活在一起的雄性

关注的变量为：

天数：雄性果蝇的寿命以天数表示。

组别：一个五级因素，其水平对应于雄性果蝇所在的组别：

“G1”：独自生活的雄性

“G2”：有一个感兴趣的雌性的雄性

“G3”：有八个感兴趣的雌性的雄性

“G4”：有一个不感兴趣的雌性的雄性

“G5”：有八个不感兴趣的雌性的雄性

Question of Interest

性活动如何影响雄性果蝇的寿命？

Read in and Inspect the Data

Fruitfly.df=read.csv("Fruitfly.csv",stringAsFactors=TRUE)

plot(days~group,data=Fruitfly.df)

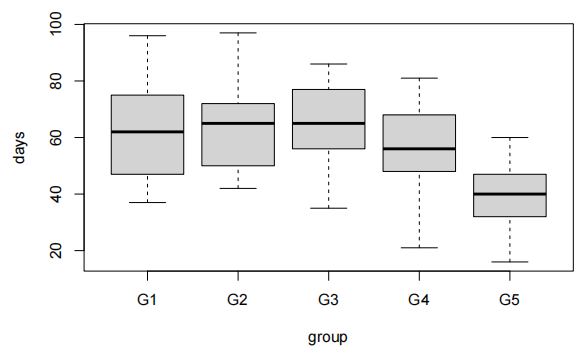
summaryStats(days~group,Fruitfly.df)

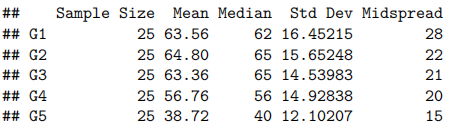
我们的假设是，与感兴趣的雌性一起生活的雄性比与感兴趣的雌性一起生活的雄性活得更长，但根据我们的数据，这一假设似乎不太可信。

Model Building and Check Assumptions

ff.fit=lm(days~group,data=Fruitfly.df)

modelcheck(ff.fit)

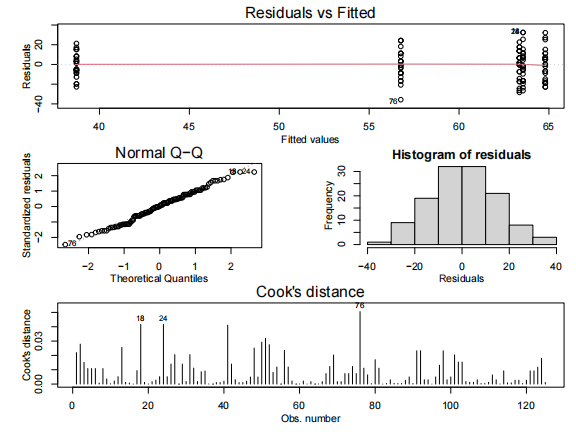
anova(ff.fit)

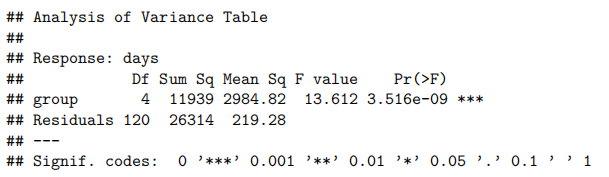
summary(ff.fit)

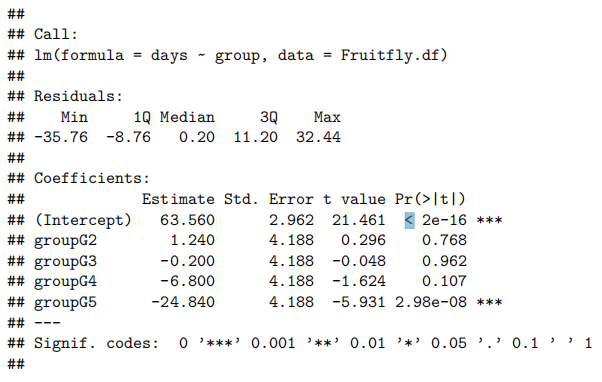
Multiple Comparisons Output

library(emeans)

Fruitfly.emm=emeans(ff.fit,~group)

#view all pairwise comparisons:

pairs(Fruitfly.emm,infer=TRUE)

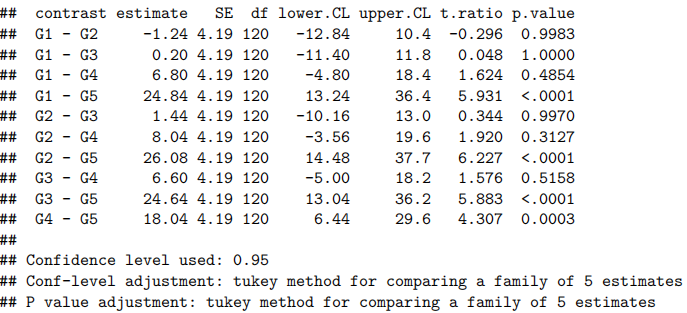
# View only the comparisons that are significant at the 5% level:

Fruitfly.pairs=data.frame(pairs(Fruitfly.emm,infer=T))

subset(Fruitfly.pairs,p.value<0.05)

Methods and Assumption Checks

按组别划分的天数箱线图显示，与其它组别相比，与8个不感兴趣的雌性共同生活的雄性寿命较短。因此，我们对这些数据拟合了一个单因素方差分析模型。

我们的最终模型是：

$d a y s_{i} = β_{0} + β_{1} \times G r o u p 2_{i} + β_{2} \times G r o u p 3_{i} + β_{3} \times G r o u p 4_{i} + β_{4} \times G r o u p 5_{i} + ε$

其中，如果第 $i$ 只雄性果蝇属于 $X$ 组，则 $G r o u p X_{i}$ 为1，否则为0， $ε_{i}$ ∼ $i i d N (0, σ^{2})$ 。

或者，我们的最终模型可以写为： $d a y s_{i j} = μ + σ_{i} + ε_{i j}$

其中 $μ$ 是总体平均生存时间， $σ_{i}$ 是处于第 $i$ 组的影响， $ε_{i}$ ∼ $i i d N (0, σ^{2})$ 。

我们的模型解释了雄性果蝇寿命变异性的31%。

Executive Summary

研究人员对性行为如何影响雄性果蝇的寿命很感兴趣。

我们发现，第5组的雄性果蝇与8只不感兴趣的雌性果蝇相比，其影响明显不同。

特别是第5组雄性动物，平均存活天数少于：

第1组雄性（独居）比其他组少活13到36天。

第2组雄性（与一只感兴趣的雌性同住）比其他组少活14到38天。

第3组雄性（与八只感兴趣的雌性同住）比其他组少活13到36天。

第4组雄性（与一只不感兴趣的雌性同住）比其他组少活6到30天。

轻松一点说，这些雄性果蝇在没有雌性存在的情况下是没问题的，或者如果雌性存在的话，它们需要对雌性“感兴趣”——否则它们会更早死亡（它们会“像苍蝇一样掉下来”）。我们很容易对人类做出类似的推断，但这可能有点过头了！

Case Study 11.2: Exam vs Degree

Problem

我们希望量化每种学位类型的统计学20x课程的预期期末考试成绩（满分100分）。特别是，我们想调查“学位”是否对期末考试成绩有影响。

感兴趣的变量包括：

考试：学生的考试成绩，满分100分。

学位：四个等级因素，对应于学生的学位——“学士”、“商学士”、“理学士”和“其他”。

Question of Interest

学生注册的学位是否与其最后20x考试成绩相关？

Read in and Inspect the Data

Stats20x.df = read.table("STATS20x.txt", header = T)

Stats20x.df$Degree=factor(Stats20x.df$Degree)

#Draw boxplot

plot(Exam ~ Degree, data = Stats20x.df)

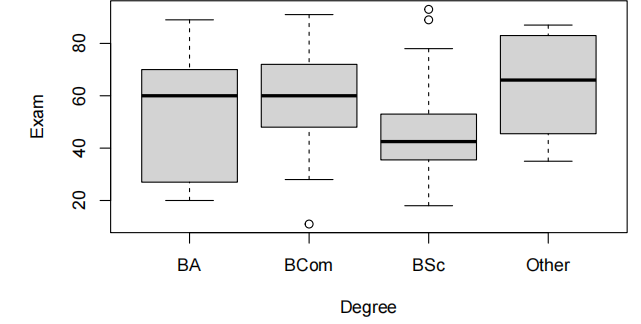
#Summary stats:

summaryStats(Exam ~ Degree, Stats20x.df)

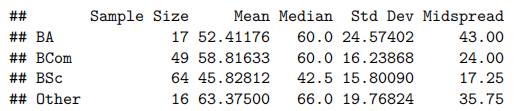
“BSc”组明显低于其他组。从最小到最大，标准差在两倍范围内，因此我们可以接受方差相等的假设。（中间分布确实超过了两倍的经验法则，因此我们在解释时可能需要谨慎。）

Model Building and Check Assumptions

degree.fit = lm(Exam ~ Degree, data = Stats20x.df)

modelcheck(degree.fit)

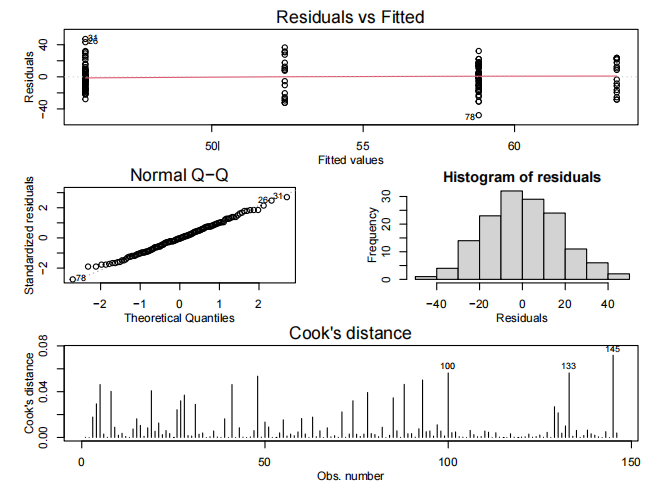
anova(degree.fit)

summary(degree.fit)

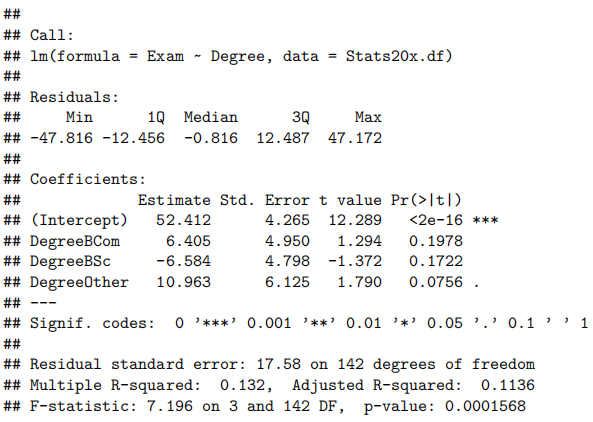
Multiple Comparisons Output

pairs(emeans(degree.fit,~Degree,infer=T))

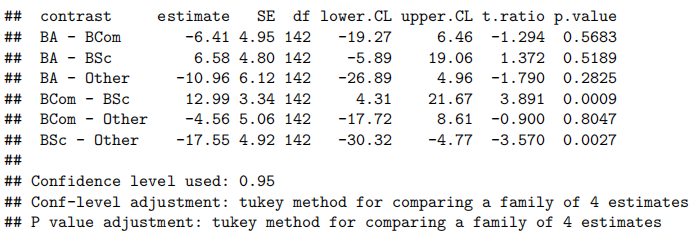
Methods and Assumption Checks

我们希望用等级来解释考试成绩，等级是一个有四个级别的因素，因此我们用单向方差分析模型拟合这些数据。

模型假设似乎得到了满足。

我们的最终模型是：

$E x a m_{i} = β_{0} + β_{1} \times D e g r e e . B C m_{i} + β_{2} \times D e g r e e . B S c_{i} + β_{3} \times D e g r e e . O t h e r_{i} + ε_{i}$

其中，如果学生注册了学位 $x$ ，则 $D e g r e e . x_{i}$ 为1，否则为0,

$x \in {B C o m ， B S c ， O t h e r}$ , $ε_{i}$ ∼ $i i d N (0, σ^{2})$ 。

或者，我们的最终模型可以写为： $E x a m_{i j} = μ + α_{i} + ε_{i j}$

其中 $μ$ 是考试总平均分， $α_{i}$ 是处于第 $i$ 个等级,

$i \in {B A ， B C o m ， B S c ， O t h e r}$ 的影响， $ε_{i}$ ∼ $𝑖 𝑖 𝑑 𝑁 (0, 𝜎^{2})$ 。

我们的模型解释了学生考试成绩变化的13.2%。

Executive Summary

学生的学位是否与其最终的20x考试成绩相关？

我们确实有证据表明，四个学位组（文学士、商学士、理学士和其他）之间的预期考试成绩并不相同。然而，我们发现的唯一显著差异是，理学士学生的成绩低于商学士和其他学位的学生。

以95%的置信度，我们可以断言：（结果来源是emeans）

平均而言，“理学士”学生比“商学士”学生差4到22分。

平均而言，“理学士”学生比“其他”学生差5到30分。

Chapter 12: Linear models with two explanatory factor variables (Two-way analysis of variance)具有两个解释因子变量的线性模型（双向方差分析）

模型定义

双因子方差分析 (Two-way ANOVA) 模型用于研究两个分类解释变量（因子 A 和因子 B）如何影响一个连续响应变量 Y。模型可以包含这两个因子的主效应以及它们之间的交互效应。

带交互效应的模型 (Interaction Model):

$E [Y] = μ + α_{i} + β_{j} + (α β)_{i j}$

$E [Y] = β_{0} + β_{1} X_{A 1} + β_{2} X_{B 1} + β_{3} X_{A 1} X_{B 1}$

其中 $α_{i}$ 是因子A第 i 水平的主效应， $β_{j}$ 是因子B第 j 水平的主效应， $(α β)_{i j}$ 是交互效应。β0 是基线组的均值，β1,β2 是主效应参数，β3 是交互效应参数。

不带交互效应的模型 (Main Effects Model / Additive Model)

$E [Y] = μ + α_{i} + β_{j}$ ，或者，在R中：

$E [Y] = β_{0} + β_{1} X_{A 1} + β_{2} X_{B 1}$ ，此模型假设两个因子对响应变量的影响是可加的。

核心思想

主效应 (Main Effects): 一个因子在另一因子各水平上平均的效应。例如，因子A的主效应是指在因子B的不同水平间取平均后，因子A各水平间的差异。

交互效应 (Interaction Effect): 一个因子对响应变量的效应依赖于另一个因子的水平。如果存在交互效应，则不能孤立地讨论一个因子的主效应。

可视化: 交互图 (Interaction plots) 可以帮助初步判断是否存在交互。若图中线条不平行，则可能存在交互效应。

模型简化: 通常从包含交互效应的完整模型开始。如果交互效应不显著，则可以简化为只包含主效应的模型 (遵循奥卡姆剃刀原则)。如果某些主效应也不显著，可以进一步简化模型。

参数解释与推断 (使用 emmeans)

带交互效应的模型:

截距项 $β_{0}$ ：当所有因子变量都处于其基线水平时，响应变量的期望均值。

主效应项（如 $β_{1}, β_{2}$ ）： for FactorAlevel1): 当另一因子 (FactorB) 处于基线水平时，FactorAlevel1 相对于 FactorA 基线水平对响应变量均值的平均改变量。

交互效应项（如 $β_{3}$ ）： for FactorAlevel1:FactorBlevel1): 当 FactorA 为 level1 且 FactorB 为 level1 时，除了它们各自的主效应之外，对响应变量均值的额外改变量。它表示 FactorA 的效应如何因 FactorB 的水平而改变。

重点: 当交互效应显著时，应主要解释在另一个因子不同水平下，一个因子的简单效应 (simple effects)，而不是主效应。这通常通过 emmeans 包进行成对比较 (pairwise comparisons) 来实现。

不带交互效应的模型 (主效应模型):

截距项 $β_{0}$ ：所有因子处于基线水平时响应变量的期望均值。

斜率项（如 $β_{1}, β_{2}$ ）：for FactorAlevel1): 不论 FactorB 处于哪个水平，FactorAlevel1 相对于 FactorA 基线水平对响应变量均值的平均改变量（因为效应是可加的）。

emmeans 包: 用于计算和比较各因子水平组合的估计边际均值 (estimated marginal means, EMMEs)，并进行调整后的成对比较，这对于解释交互效应和主效应至关重要。它能提供置信区间和p值。

假设检验 / 模型评估

1.交互效应检验

通过 anova(model) 查看交互项 (如 FactorA:FactorB) 的F检验结果。若p值小于显著性水平 (如 0.05)，则认为交互效应显著。

2.主效应检验

若交互效应不显著，则在主效应模型中通过 anova(model) 查看各主效应的F检验结果。

若交互效应显著，则主效应的解释需谨慎，应结合交互作用来分析。

3.模型拟合

$R^{2}$ 和调整 $R^{2} (A d j u s t e d R^{2})$ 衡量模型解释的变异程度。

4.成对比较 (Pairwise Comparisons)

使用 emmeans 包中的 pairs() 函数进行。当交互效应显著时，比较一个因子在另一个因子固定水平下的各水平间差异。当交互效应不显著但主效应显著时，比较该主效应各水平间的总体差异。

displayPairs() (s20x包) 可以帮助展示组内比较。

数据特征与模型假设

数据特征:

响应变量 (Y) 为连续型。
解释变量为两个或多个分类型因子变量。

模型假设 (与线性回归类似):

独立性 (Independence): 观测值之间相互独立。
正态性 (Normality): 各组内残差服从正态分布。可通过 normcheck(model) 检验。
等方差性 (Equal Variances / Homoscedasticity - EOV): 不同因子水平组合下，响应变量的方差相同（即残差方差齐性）。可通过 plot(model, which=1) (残差对拟合值图) 检验。
无异常影响点 (No Unduly Influential Data Points): 可通过 cooks20x(model) 检测。

例题分析：考试分数 (Exam Score Analysis)

例题1：考试分数 vs 测试通过情况 (Pass.test) 与出勤情况 (Attend)

总览： 本例旨在研究学生的测试通过情况 (Pass.test) 和出勤规律性 (Attend) 如何共同影响其最终考试分数 (Exam)，并特别关注这两个因素之间是否存在交互效应。

变量类型与转换：

响应变量：Exam (考试分数，连续型)。
解释变量：Attend (出勤情况)：分类变量，在R中需确保其为因子类型(levels: No, Yes)。原始数据中可能已是或需用 factor() 函数转换。

Attend (出勤情况)：分类变量，在R中需确保其为因子类型 (levels: No, Yes)。原始数据中可能已是或需用 factor() 函数转换。

# 假设 Stats20x.df$Attend 已从数据文件读入 S

tats20x.df$Attend <- factor(Stats20x.df$Attend)

Pass.test (测试通过情况)：分类变量 (levels: nopass, pass)。这是根据原始数值型变量 Test 创建的：当 Test >= 10 时为 "pass"，否则为 "nopass"。创建后也需转换为因子。

Stats20x.df$Pass.test<-factor(ifelse(Stats20x.df$Test>=10,"pass", "nopass"))

探索性数据分析：绘制交互图以初步判断是否存在交互效应

# library(s20x) # 如果 interactionPlots 是 s20x 包的

interactionPlots(Exam ~ Pass.test + Attend, data = Stats20x.df)

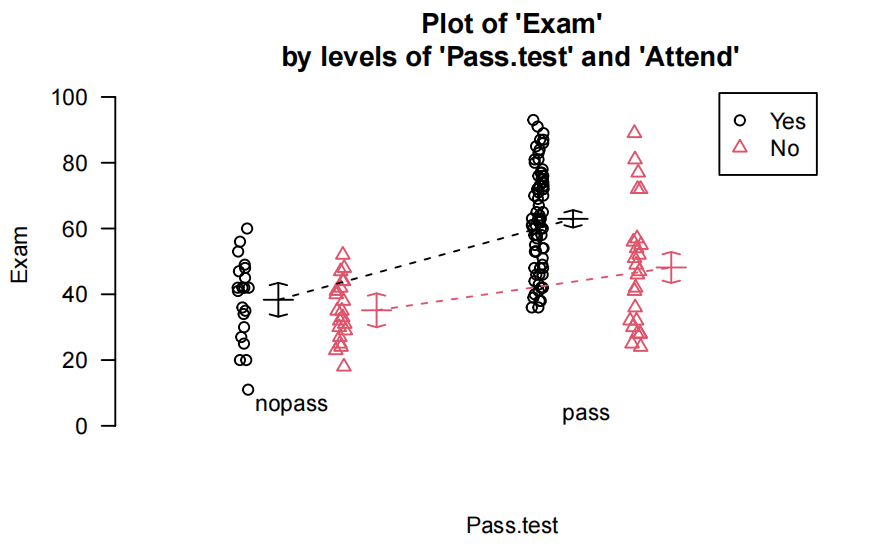
交互图显示，代表不同出勤情况的线条呈现不平行状态。具体来说，对于通过测试的学生，出勤与否的差异似乎比未通过测试的学生更大。这初步表明 Pass.test 和 Attend 之间可能存在交互效应，即测试通过情况对考试分数的影响可能因出勤情况的不同而异。

模型拟合与简化：

1.拟合含交互项的模型： 我们首先拟合包含 Attend、Pass.test 主效应以及它们之间交互效应 (Attend:Pass.test) 的模型。

Exam.fit <- lm(Exam ~ Attend * Pass.test, data = Stats20x.df)

# Attend * Pass.test 在公式中等价于 Attend + Pass.test + Attend:Pass.test

2.模型诊断：对 Exam.fit 模型进行诊断，以检验其是否满足基本假设

残差对拟合值图 (检查方差齐性 EOV):

plot(Exam.fit, which = 1)

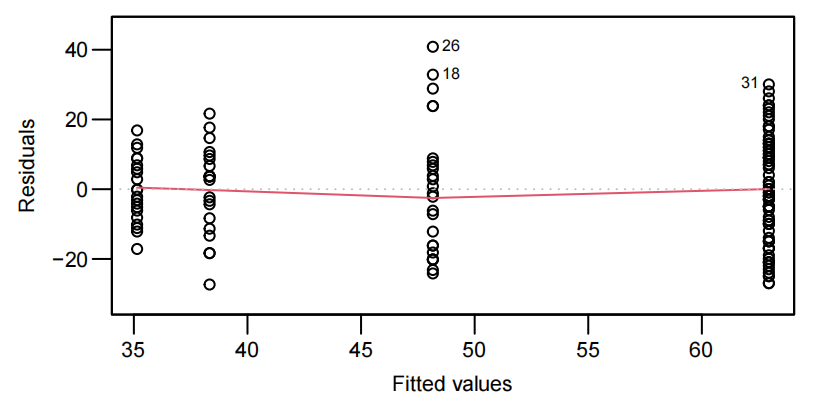
图中点的散布应随机，没有明显的模式（如喇叭形），表明方差基本齐性。教材中认为此假设满足。

正态QQ图 (检查残差正态性)：

normcheck(Exam.fit) # 或者 plot(Exam.fit, which = 2)

点应大致落在直线上，表明残差基本符合正态分布。教材中认为此假设满足，尽管可能在尾部略有偏离。

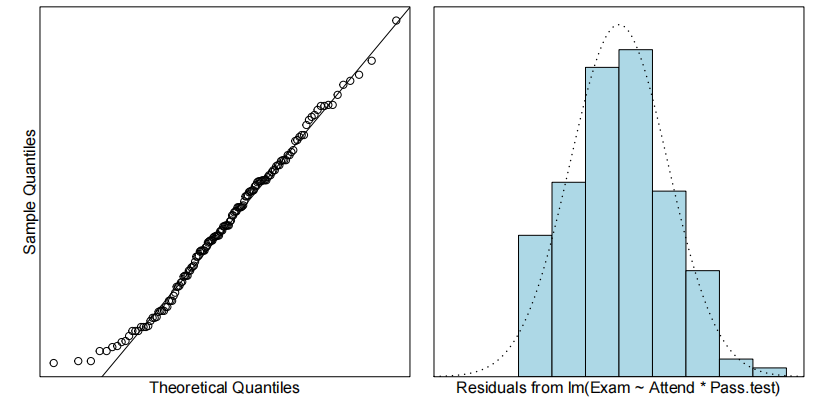
Cook's距离图 (检查强影响点)：

cooks20x(Exam.fit)

图中没有Cook's距离异常大的点，表明无单个观测点对模型结果产生过大影响。诊断结果表明模型假设基本得到满足，后续的推断结果可信。

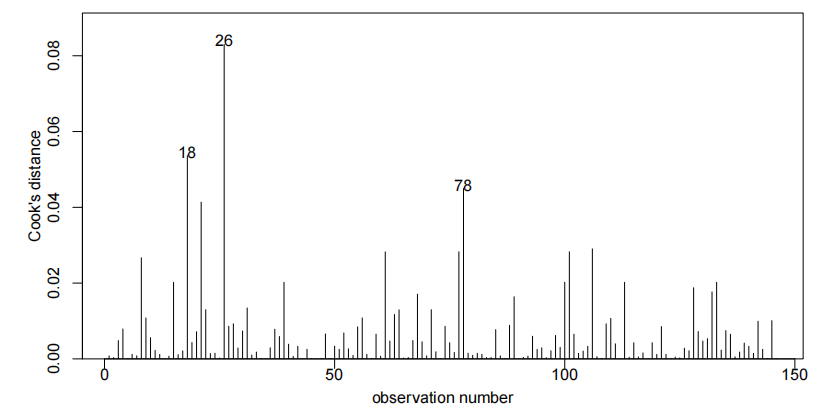
3.ANOVA 检验交互项：

使用 anova() 函数查看模型中各项的显著性，特别是交互项。

anova(Exam.fit)

输出的ANOVA表会包含 Attend:Pass.test 交互项的F统计量和p值。教材中此交互项的p值为0.04297。

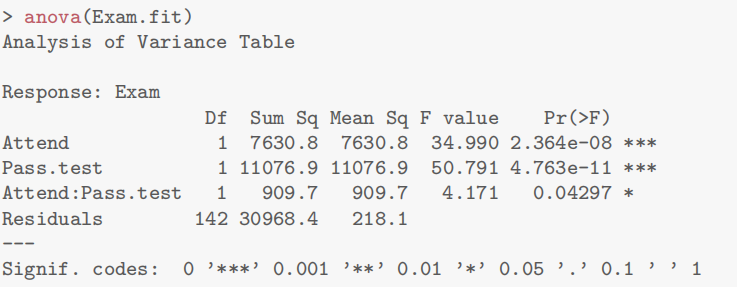
模型确定： 由于交互项的p值 (0.04297) 小于常用的显著性水平0.05，我们认为交互效应是统计显著的。因此，应保留交互项在模型中，最终解释模型即为 Exam.fit。

结果解释 (基于 Exam.fit 和 95% 置信区间)： 由于交互效应显著，我们不能孤立地讨论出勤或测试通过情况的单一主效应，而必须结合另一个因素的水平来解释其效应。这时，使用 emmeans 包进行成对比较非常有用，它可以帮助我们理解在某个因子特定水平下，另一个因子不同水平间的均值差异。

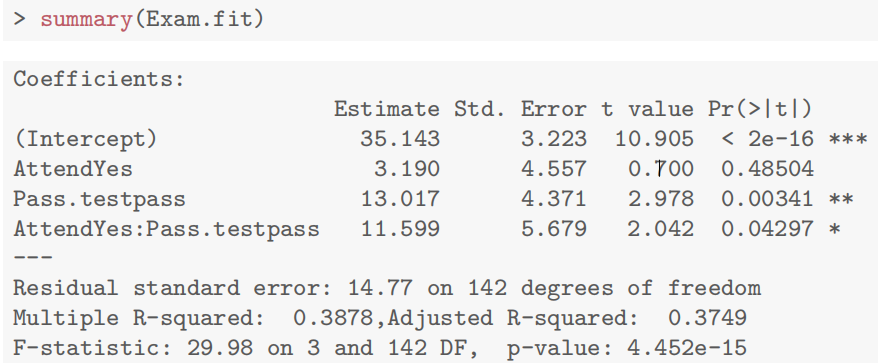
library(emmeans)

# 计算 Attend 和 Pass.test 各组合的估计边际均值

exam.emm <- emmeans(Exam.fit, ~ Attend * Pass.test)

# 进行所有可能的成对比较，并获取置信区间和调整后的p值

exam.pairs <- pairs(exam.emm, infer = TRUE)

print(exam.pairs)

[!success]

什么是emmeans

emmeans全称是Estimated Marginal Means，估计边际均值。主要用于在统计模型中计算调整后的均值，进行事后比较或者多重比较。用户可能是在进行方差分析或者混合效应模型后，想要比较不同组别之间的差异，这时候emmeans就很有用了。首先，要解释emmeans的功能。比如，它可以在控制其他变量后，估计因变量在不同因子水平上的均值，还能进行多重比较，生成置信区间和p值。

边际均值（Marginal Means）的直观解释

在统计学中，边际均值（Marginal Means） 也称为调整均值（Adjusted Means） 或最小二乘均值（Least Squares Means），是一种在控制其他变量影响后计算的平均值。它在实验设计和方差分析中非常重要，尤其适用于处理不平衡数据或有交互作用的模型。

为什么需要边际均值？

传统的组均值（Raw Means）直接计算每组数据的平均值，但在复杂实验中可能存在问题：

数据不平衡：各组样本量不同时，直接平均会偏向样本量大的组。

变量交互：当变量之间存在交互作用时，简单均值无法反映真实效应。

协变量影响：需要控制其他变量（如年龄、性别）的干扰。

边际均值通过统计模型（如线性模型、GLM）调整这些因素，提供更 “公平” 的组间比较。

合起来就是

exam.pairs<-pairs(emmeans(Exam.fit,~Attend*Pass.Test),infer=T)

exam.pairs

# 教材中可能使用 s20x 包的 displayPairs 函数来更清晰地展示特定组内比较：

# displayPairs(exam.pairs, by = "Attend")

# 比较在不同Attend水平下Pass.test的效应

# displayPairs(exam.pairs, by = "Pass.test")

# 比较在不同Pass.test水平下Attend的效应

通常（在本课程中）我们只对同一水平内的比较感兴趣。也就是说，比较两个被比较的处理组合时，两者之间有一个共同的水平（也就是控制变量，displayPairs(exam.pairs, c("No","Yes"), c("nopass","pass"))）。

根据教材中对 emmeans 输出（其实是displayPairs）的解读（通常关注特定条件下的比较和其95%置信区间）：

对于规律出勤 (Attend=Yes) 的学生： 通过测试 (Pass.test=pass) 的学生比未通过测试 (Pass.test=nopass) 的学生，预期考试分数平均高出约24.62分 (教材中估计差异为-24.616，比较的是nopass vs pass，这里调整为pass vs nopass)，95%置信区间约为 (15.19, 34.04) 分。
对于不规律出勤 (Attend=No) 的学生： 通过测试的学生比未通过测试的学生，预期考试分数平均高出约13.02分，95%置信区间约为 (1.65, 24.38) 分。
对于通过测试 (Pass.test=pass) 的学生： 规律出勤 (Attend=Yes) 的学生比不规律出勤 (Attend=No) 的学生，预期考试分数平均高出约14.79分，95%置信区间约为 (5.98, 23.60) 分。
对于未通过测试 (Pass.test=nopass) 的学生： 规律出勤的学生与不规律出勤的学生相比，预期考试分数平均高出约3.19分，但此差异不统计显著，其95%置信区间为 (-8.66, 15.04) 分，该区间包含0。

（也就相当于emmeans中两个变量都发生变化的那几行就不看，要控制变量）

例题2：考试分数 vs 性别 (Gender) 与出勤情况 (Attend)

总览： 本例旨在研究学生的性别 (Gender) 和出勤规律性 (Attend) 如何共同影响其最终考试分数 (Exam)，并检验这两个因素之间是否存在交互效应。

变量类型与转换：

响应变量：Exam (考试分数，连续型)。

解释变量：

Attend (出勤情况)：分类变量，已转换为因子 (levels: No, Yes)。
Gender (性别)：分类变量 (如 Female/Male)，需确保其为因子类型。

探索性数据分析： 绘制交互图

interactionPlots(Exam ~ Attend + Gender, data = Stats20x.df)

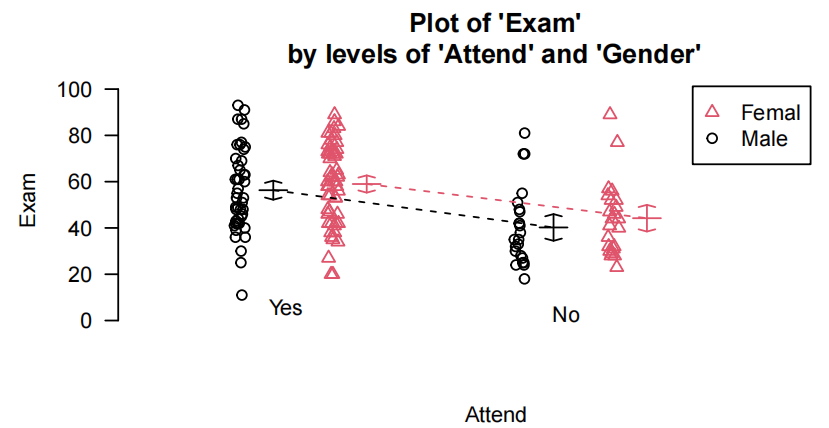
交互图显示，代表不同性别的线条大致平行。这初步表明 Attend 和 Gender 之间可能没有显著的交互效应，即出勤对考试分数的影响对于不同性别可能是相似的，反之亦然。

模型拟合与简化：

拟合含交互项的模型：

Exam.fit2 <- lm(Exam ~ Attend * Gender, data = Stats20x.df)

模型诊断： 对 Exam.fit2 进行与例题1类似的诊断（残差图plot、正态性检验normcheck、Cook's距离cooks20x）。教材中指出假设检查基本满足。

ANOVA 检验交互项：（教材分步去影响因素，先去交互项再去主效应项Gender，实际上我觉得可以一步到位没必要分开来，还得换模型lm然后summary）

anova(Exam.fit2)

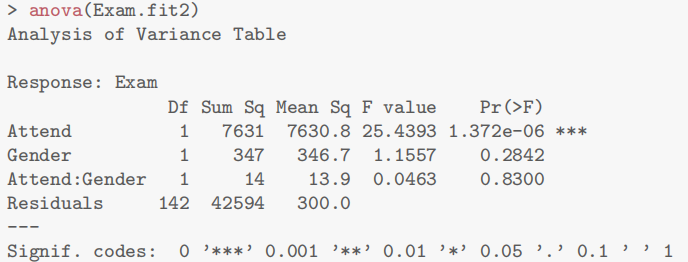
ANOVA表显示 Attend:Gender 交互项的p值为0.8300，Gender也只有0.2842，统统去掉。

Exam.fit4 <- lm(Exam ~ Attend, data = Stats20x.df)

模型 Exam.fit4 是最终选定的最简洁且有效的模型。这实际上简化成了一个单因子方差分析（或等价于两样本t检验）。

结果解释 (基于最终模型 Exam.fit4 和 95% 置信区间)： 我们解释最终模型 Exam.fit4 的结果。

summary(Exam.fit4)

confint(Exam.fit4)

summary(Exam.fit4) 的输出显示：

截距项 ((Intercept)) 的估计值为 42.217，这是当 Attend 为基线水平 ("No") 时的预期考试分数。AttendYes 的系数估计值为 15.563。这意味着，规律出勤 (Attend=Yes) 的学生比不规律出勤 (Attend=No) 的学生，其平均考试分数预计高出 15.563 分。
confint(Exam.fit4) 给出的 AttendYes 的95%置信区间为 (9.480749, 21.64447)。因此，我们可以有95%的信心认为，规律出勤的学生平均考试分数比不规律出勤的学生高出 9.48 到 21.64 分。

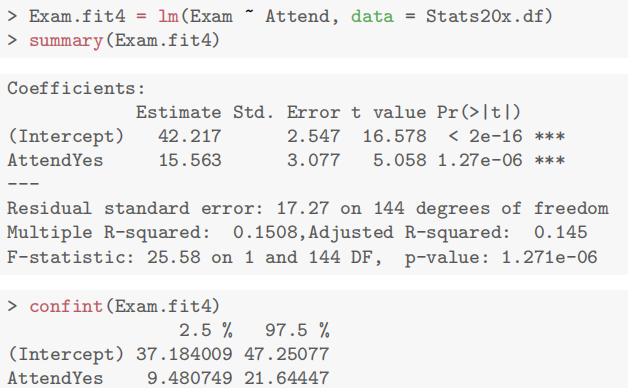
第十二章R语言代码总结

1.使用交互图检查数据。非平行线表示可能存在交互作用。

interactionPlots(Exam ~ Pass.test + Attend, data = Stats20x.df)

[!success]

前面已经学过的：

拟合交互作用模型（在模型公式中使用*）

Exam.fit = lm(Exam ~ Attend*Pass.test, data = Stats20x.df)

并使用ANOVA表来查看是否存在交互作用的证据

anova(ExamTestAttend.fit)

2.emmeans+pairs得出成对变量的估计边际均值并作两两比较

exam.pairs = pairs(emmeans(Exam.fit, ~ Attend*Pass.test), infer=T)

displayPairs(exam.pairs, c("No","Yes"), c("nopass","pass"))

Case Study 12.1: Exam vs Test & Attendance

Problem

我们希望确定定期出勤和通过考试是否与考试成绩相关。我们已经观察到，通过考试和定期出勤平均可以提高获得好成绩的机会。

感兴趣的变量包括：

考试：总分为100分的考试成绩。

出勤：一个二元因素，分为“是”和“否”。

通过考试：一个二元因素，分为“是”和“否”。

Question of Interest

我们对期末考试成绩和通过考试之间的关系感兴趣，以及这种关系是否因学生是否经常参加讲座而不同。

Read in and Inspect the Data

Stats20x.df = read.table("STATS20x.txt", header = T)

head(Stats20x.df)

#因此，我们需要使用Test变量来创建名为Pass.test的变量。

Stats20x.df$Pass.test = factor(ifelse(Stats20x.df$Test >= 10, "pass", "nopass"))

#检查新变量Pass.test是否正确生成

min(Stats20x.df$Test[Stats20x.df$Pass.test == "pass"])

## [1] 10

max(Stats20x.df$Test[Stats20x.df$Pass.test == "nopass"])

## [1] 9.1

interactionPlots(Exam ~ Pass.test + Attend, data = Stats20x.df)

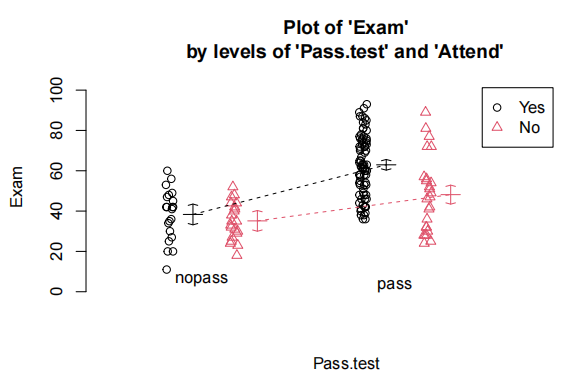
#也可以反过来查看交互图：

interactionPlots(Exam ~ Attend + Pass.test, data = Stats20x.df)

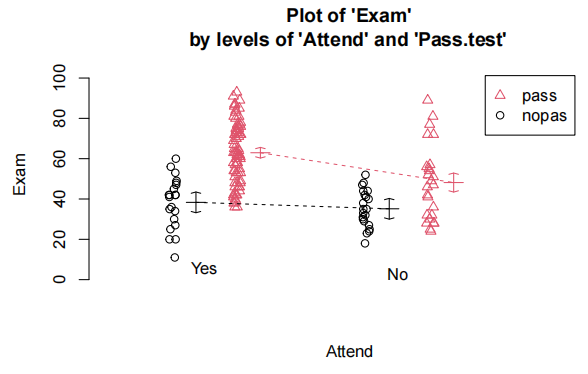
通过考试的学生的考试成绩比未通过的学生更高。然而，这种差异在参加讲座的学生中比未参加的学生中更为显著，这从交互图中的非平行色线可以看出。换句话说，通过考试的影响因是否参加讲座而异，这表明两个预测变量之间可能存在交互作用。

Model Building and Check Assumptions

Exam.fit<-lm(Exam~Attend*Pass.test,data=Stats20x.df)

#模型公式也可以是：Exam ~ Attend + Pass.test + Attend:Past.test

plot(Exam.fit,which=1)

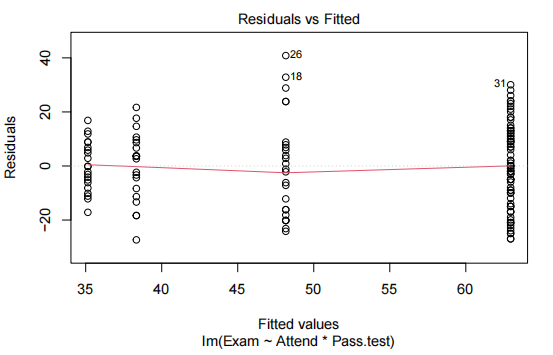
normcheck(Exam.fit)

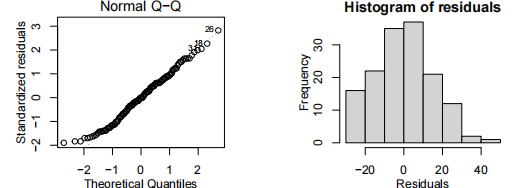
cooks20x(Exam.fit)

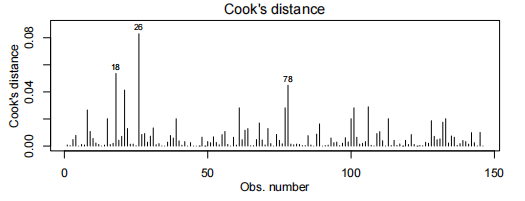
anova(Exam.fit)

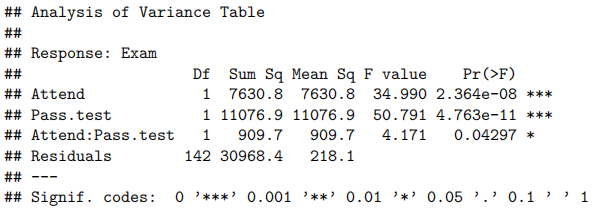
summary(Exam.fit)

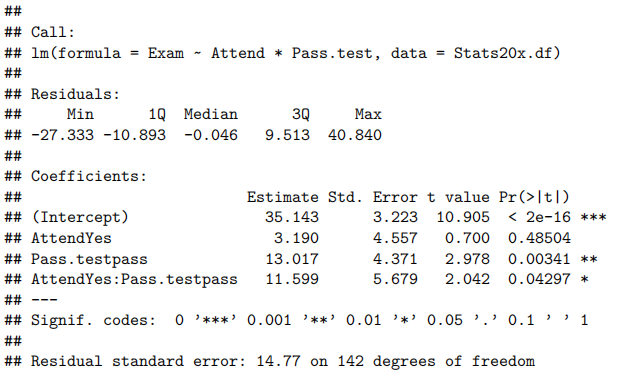
## Multiple R-squared: 0.3878, Adjusted R-squared: 0.3749

## F-statistic: 29.98 on 3 and 142 DF, p-value: 4.452e-15

Paiwise comparisons

library(emmeans)

Exam.pairs<-pairs(emmeans(Exam.fit,~Attend*Pass.test),infet=T)

Exam.pairs

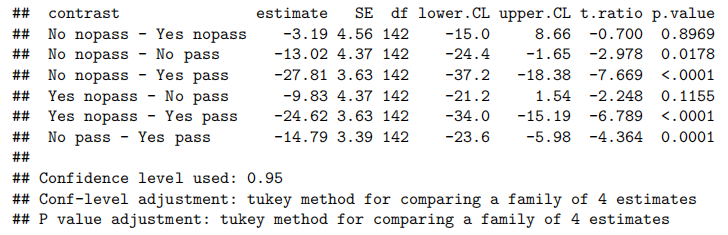
Methods and Assumption Checks

我们有两个解释变量Pass.test和Attend，以及一个数值响应变量Exam，因此我们拟合了一个包含交互项的双向方差分析模型。交互项显著（P值= 0.04)，因此被保留在模型中。

模型的假设似乎得到了满足。

我们的最终模型是:

$E x a m_{i} = β_{0} + β_{1} \times T e s t . p a s s_{i} + β_{2} \times A t t e n d . Y e s_{i} + β_{3} \times T e s t . p a s s_{i} \times A t t e n d . Y e s_{i} + ϵ_{i}$

其中， $T e s t . p a s s_{i}$ 和 $A t t e n d . Y e s_{i}$ 是虚拟变量，当学生 $i$ 通过考试或定期参加讲座时取值1，否则为0；而 $ε_{i} \sim i i d N （ 0 ， σ ² ）$ 。

或者，我们的最终模型可以表示为: $E x a m_{i j k} = µ + α_{i} + β_{j} + γ_{i j} + ϵ_{i j k}$

其中， $E x a m_{i j k}$ 表示学生k在考试通过组i和出勤组j中的成绩；μ代表总体平均考试成绩， $α_{i}$ 表示学生是否通过考试的影响，βj表示学生是否经常参加讲座的影响，γij表示学生通过考试与出勤情况的交互影响，而ϵijk∼iid N（0，σ 2）。这里，i∈{通过，不通过}和j∈{是，否}。

我们的模型解释了学生考试成绩的39%的变异性。

Executive Summary

我们关注期末考试成绩与通过测试之间的关系，以及这种关系是否因学生是否经常参加讲座而有所不同。

我们有证据表明，考试成绩与通过测试状态之间的关系确实取决于出勤情况。

我们估计：

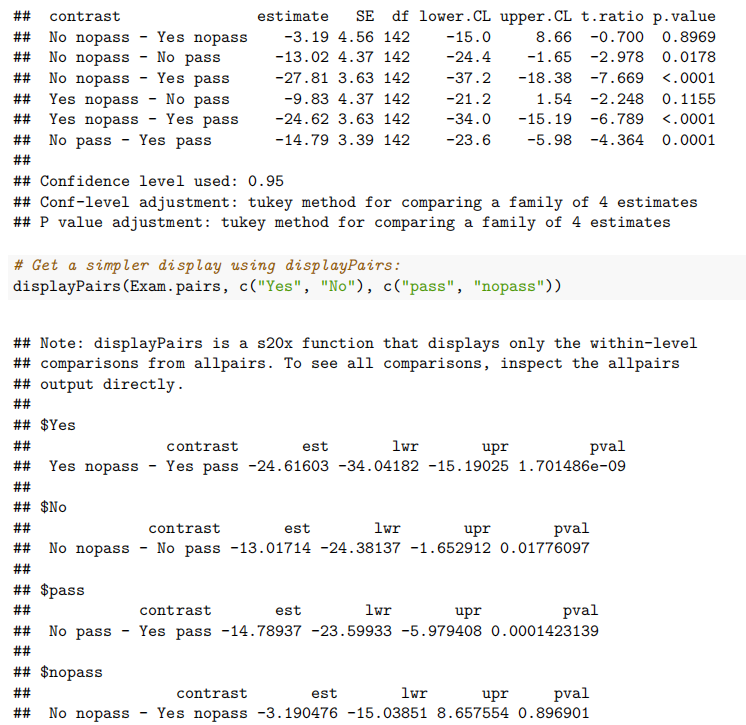
在定期参加考试的学生中，通过考试的学生平均成绩比未通过的学生高出15到34分。
在不经常参加考试的学生中，通过考试的学生平均成绩比未通过的学生高出2到24分。
在通过考试的学生中，定期参加考试的学生平均成绩比不定期参加考试的学生高出6到24分。

Case Study 12.2: Impact of a cyclone on coral reefs

Problem

澳大利亚海洋科学研究所负责监测大堡礁沿线的珊瑚和鱼类群落。这些数据包括从不同珊瑚礁地点的水下视频调查中记录的硬珊瑚覆盖百分比。1997年，热带气旋“贾斯汀”影响了大堡礁的部分区域。我们希望研究这次气旋对珊瑚覆盖的影响。

这种设计被称为BACI设计，即前后对照、控制与影响。其中一个因素是时间，分为前后两个阶段；另一个因素是珊瑚礁（或地点），分为对照组和影响组。互动意味着珊瑚覆盖面积随时间的变化在对照组和受影响区域之间存在差异。在此研究中，被归类为受影响的区域是外礁，这些区域承受着风暴的主要冲击。

感兴趣的变量包括：

覆盖率：珊瑚礁中硬珊瑚的覆盖百分比。
珊瑚礁：一个包含控制组和影响组的两水平因素。
时间：一个包含前后两个时间点的两水平因素。

Research question

飓风贾斯汀对受影响地点的珊瑚覆盖有什么影响？

Read in and Inspect the Data

Reef.df = read.csv("Reef.csv")

Reef.df = transform(Reef.df, Reef=factor(Reef), Time=factor(Time))

interactionPlots(Cover ~ Reef + Time, data = Reef.df)

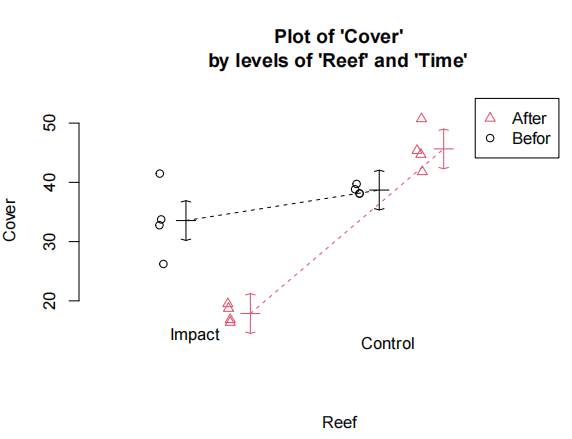
#也可以反过来查看交互图：

interactionPlots(Cover ~ Time + Reef, data = Reef.df)

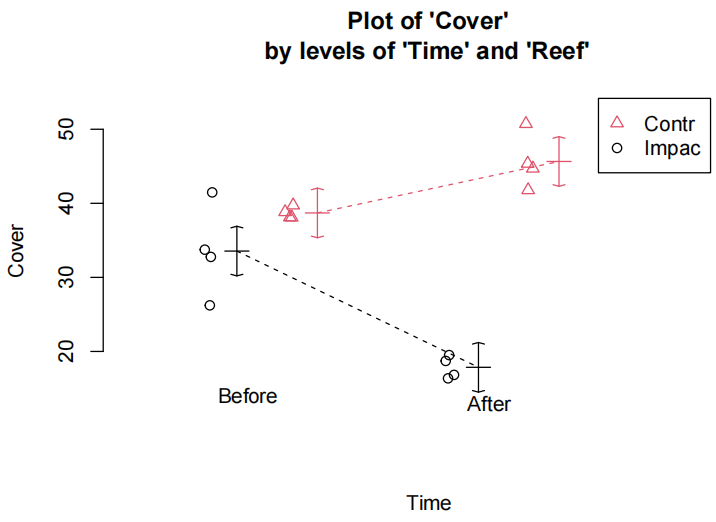
珊瑚覆盖度随时间的变化趋势在受影响的珊瑚礁和对照珊瑚礁之间有所不同。在飓风贾斯汀之前，两类珊瑚礁的覆盖度相似。然而，对于对照珊瑚礁，覆盖度在飓风后有所增加；而对于受影响珊瑚礁，覆盖度则有所减少。从彩色线条的高度不平行可以看出，我们推测时间和珊瑚礁类型之间存在相互作用。

Model Building and Check Assumptions

Cover.fiy<-lm(Cover~Time*Reaf,data=Reaf.df)

plot(Cover.fit,which=1)

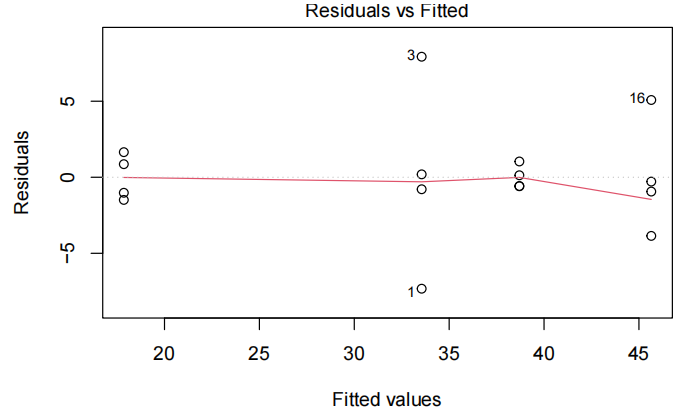
normcheck(Cover.fit)

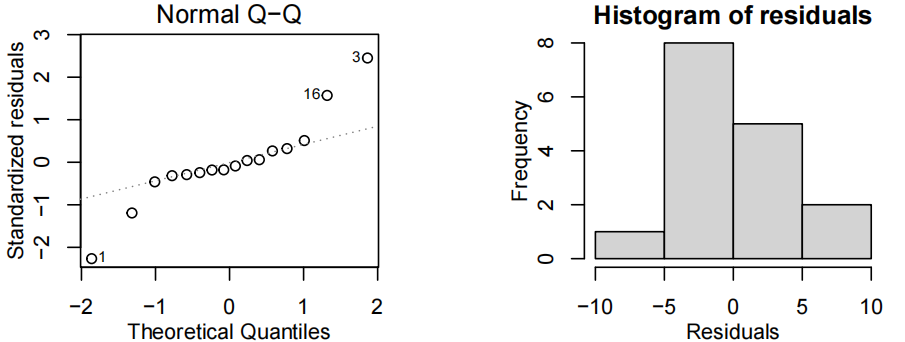
cooks20x(Cover.fit)

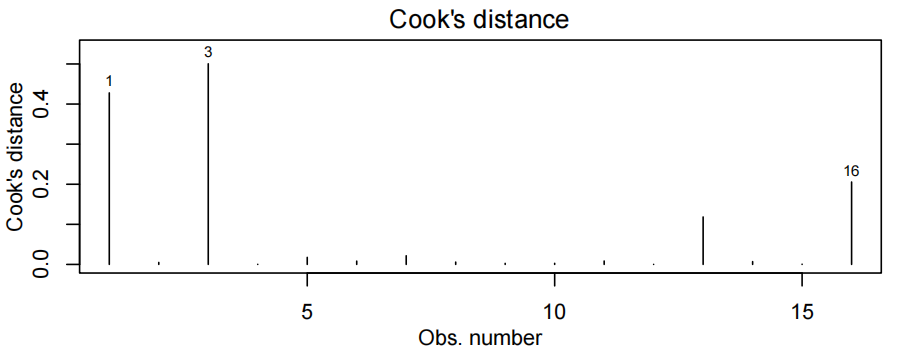
anova(Cover.fit)

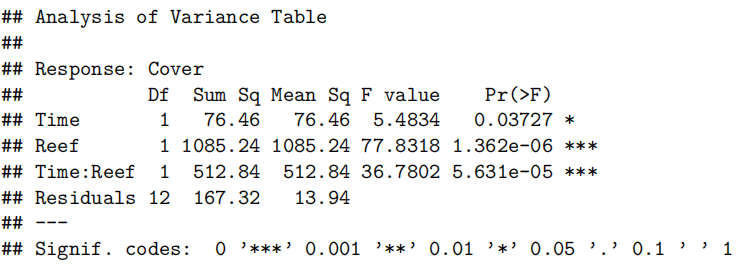
summary(Cover.fit)

##

## Call:

## lm(formula = Cover ~ Time * Reef, data = Reef.df)

##

## Residuals:

## Min 1Q Median 3Q Max

## -7.3282 -0.9609 -0.4308 0.9049 7.9257

Pairwise comparisons using emmeans

Cover.pairs<-pairs(emmeans(Cover.fit,~Time*Reaf),infer=T)

# Simplify the display:

displayPairs(Cover.pairs, c("Before", "After"), c("Control", "Impact"))

Methods and Assumption Checks

我们有一个数值响应变量Cover，以及两个解释因素Reef和Time。因此，我们构建了一个包含Reef与Time交互作用的双向方差分析模型。交互项显著（P值< 0.001)，因此被保留。

假设检验总体合理，只是Cook距离在几个点上超过了0.4。不过这并不严重，因为没有明显的异常值。当数据集仅有16个观测值时，部分数据点影响较大也不足为奇。

我们的最终模型是:

$C o v e r i = β_{0} + β_{1} \times T i m e . B e f o r e_{i} + β_{2} \times R e e f . I m p a c t_{i} + β_{3} \times T i m e . B e f o r e_{i} \times R e e f . I m p a c t_{i} + ϵ_{i}$

其中， $T i m e . B e f o r e_{i}$ 和 $r e e f . I m p a c t_{i}$ 是虚拟变量，当观测值i分别记录于飓风贾斯汀之前或位于受冲击的珊瑚礁区域时，其取值为1；其余情况下取值为0；而 $ϵ_{i} \sim i i d N （ 0 ， σ ² ）$ 。

我们的模型解释了珊瑚覆盖测量值的91%的变化。

Executive Summary

我们的目标是调查旋风贾斯汀对受影响的珊瑚礁地点珊瑚覆盖的影响。

在飓风贾斯汀之前，没有证据表明受影响的地点和控制地点之间的珊瑚覆盖量平均数量有差异。然而，在飓风过后，有强有力的证据表明两者之间存在差异。

我们估计，受气旋影响的珊瑚礁的平均珊瑚覆盖率比气旋前低8到24个百分点。相比之下，对照珊瑚礁的平均珊瑚覆盖率没有下降（事实上，有微弱的证据表明有所增加）。

在气旋过后，我们估计对照珊瑚礁的平均珊瑚覆盖率比受影响珊瑚礁高出20到36个百分点。

Case Study 12.3: Extracting dietary supplements from seaweed

Problem

岩藻多糖是一种膳食补充剂，存在于几种褐藻中，包括入侵物种Undaria，现在在新西兰广泛分布。

Undaria被入侵的一个积极面是，它可能成为一种有价值的岩藻多糖来源。这些数据来自一项研究，该研究调查了在不同实验室条件下从Undaria中提取岩藻多糖的产量。

响应变量是HikDa（基于分子量的测量），解释变量包括两个因素变量：fTemp（温度水平）和fTime（时间水平），每个变量都有三个不同的水平（three-level factor）。

关注的变量包括：

HiKda：基于分子量的测量方法。
fTemp：三级因素，包含“60”、“70”和“80”三个等级。
fTime：三级因素，包含“2”、“3”和“4”三个等级。

Question of Interest

我们希望确定Undaria中岩藻多糖的产量如何依赖于温度和时间水平，以及这些因素是否相互影响。

Read in and Inspect the Data

# The call for tab delimited data
Weed.df = read.table("Weed.txt", header = TRUE, sep = "\t")
# Several R commands to subset the data for answering the question of interest:
WeedDf = transform(Weed.df, logAlg = log(Alg), Ratio = as.character(Ratio))
WeedDf = transform(WeedDf, Ratio = as.numeric(substr(Ratio, 3, nchar(Ratio))))
WeedDf = transform(WeedDf, fTime = factor(Time), fTemp = factor(Temp),
fRatio = factor(Ratio))
KdaDf = subset(WeedDf, subset = (!is.na(HiKda)))
interactionPlots(HiKda ~ fTemp + fTime, data = KdaDf)

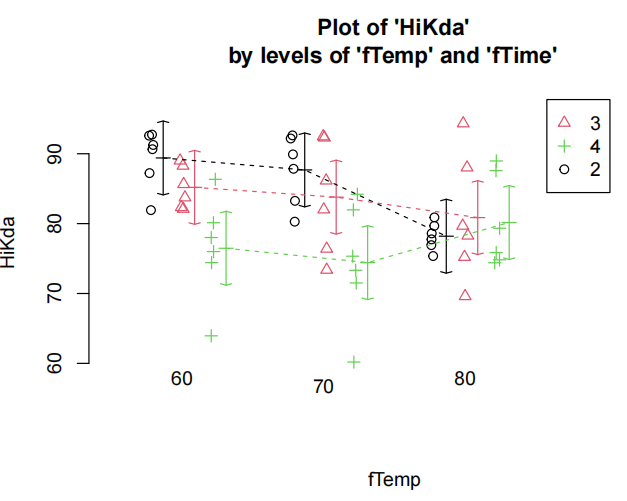
# Also look at the interaction plot the other way around:

interactionPlots(HiKda ~ fTime + fTemp, data = KdaDf)

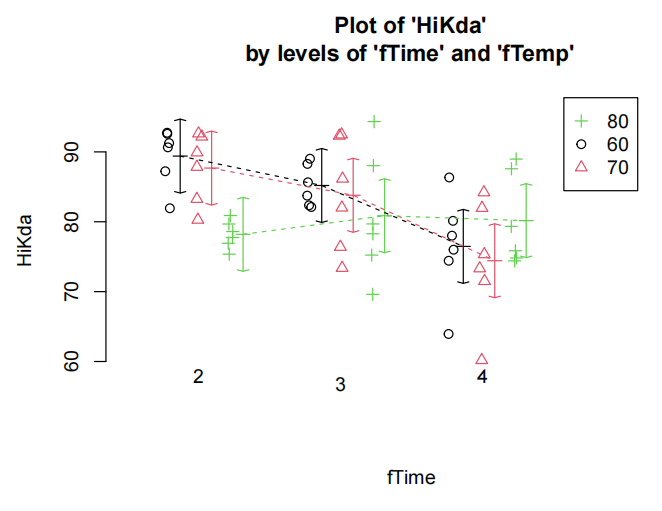
由于非平行线，建议进行交互作用分析。当温度为80度时，所有时间水平的产量相似。当温度为60和70度时，随着时间增加，产量下降。

Model Building and Check Assumptions

Kda.lm = lm(HiKda ~ fTime * fTemp, data = KdaDf)

plot(Kda.lm, which=1)

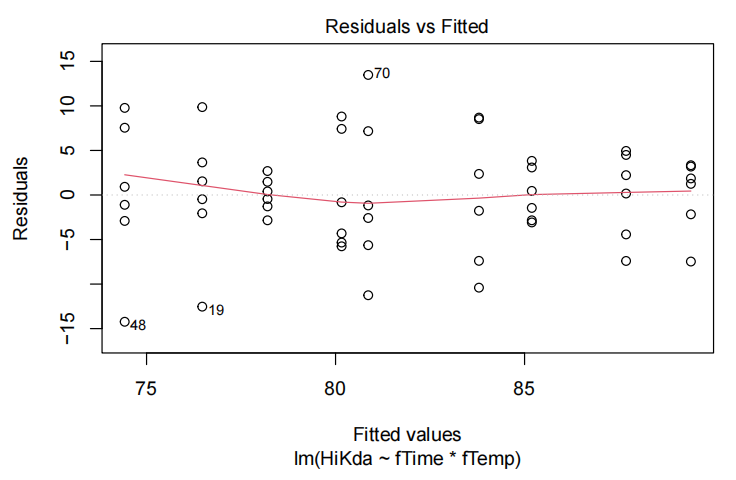
normcheck(Kda.lm)

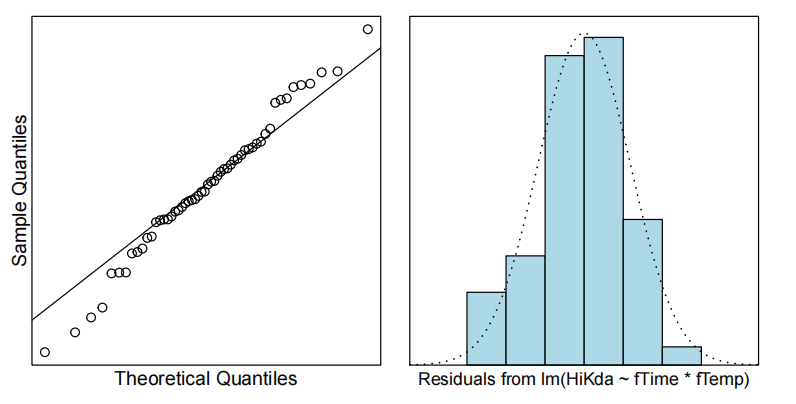
cooks20x(Kda.lm)

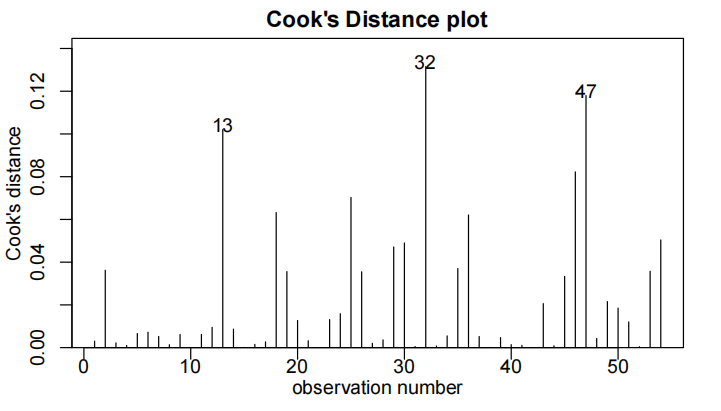
anova(Kda.lm)

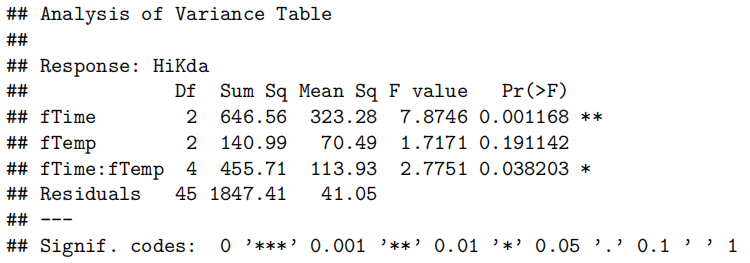
summary(Kda.lm)

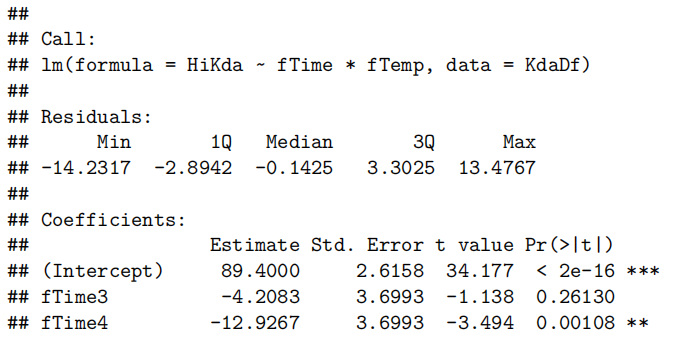
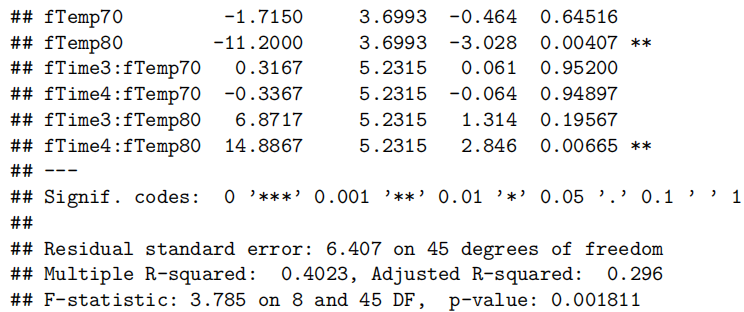
Pairwise comparisons

Kda.pairs = pairs(emmeans(Kda.lm, ~ fTime*fTemp), infer=T)
# Simplify the display of pairwise comparisons.
# Because factor levels are numbers, need to enter as "fTime2", "fTime3", etc:
displayPairs(Kda.pairs, c("fTime2", "fTime3", "fTime4"), c("fTemp60", "fTemp70", "fTemp80"))

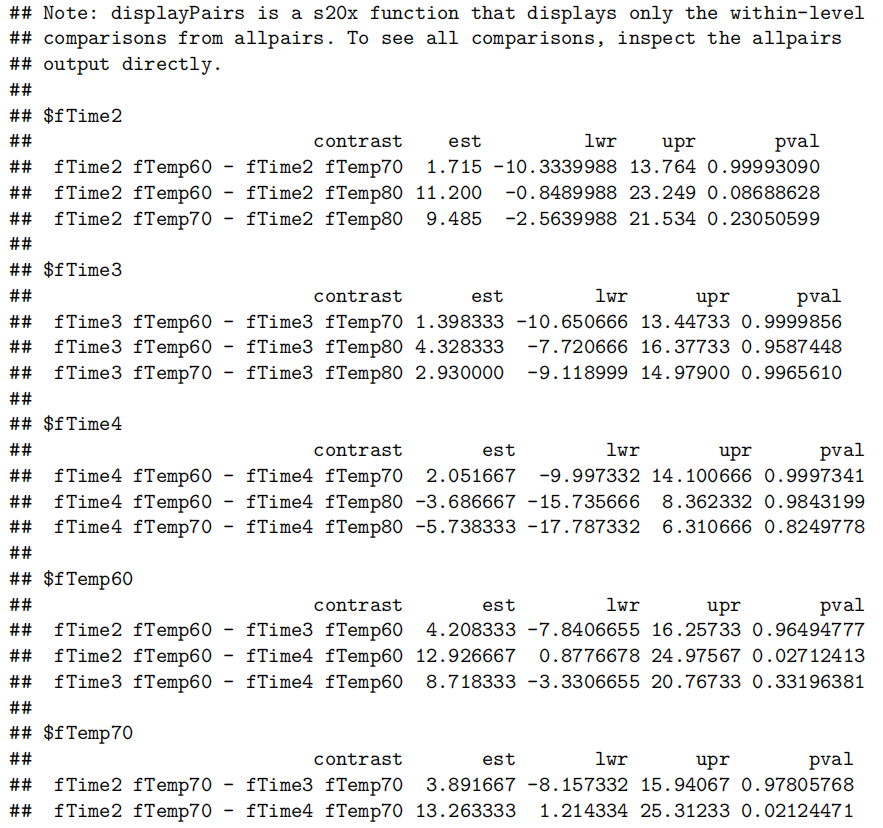
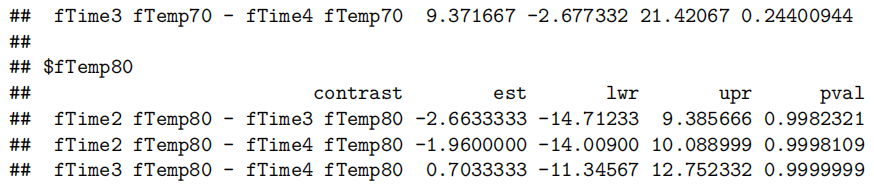
Methods and Assumption Checks

我们有一个数值响应变量HiKda，以及两个解释因素fTime和fTemp。因此，我们拟合了一个包含交互作用的双向方差分析模型。交互作用项显著（P值=0.04)，因此被保留在最终模型中。

模型假设已满足。最终模型为:

$H i K d a_{i} = β_{0} + β_{1} \times f T i m e_{i} + β_{2} \times f T e m p_{i} + β_{3} \times f T e m p_{i} \times f T i m e_{i} + ϵ_{i}$

其中 $β_{0}$ 表示总体平均产量， $f T i m e_{i}$ 代表第i个时间点的影响， $f T e m p_{i}$ 表示第i个温度的影响，γij是第i个时间点与第j个温度组合的交互效应，而ϵijk∼服从独立同分布N（0，σ²）。

我们的模型解释了产量（HiKda）的40%的变异性。

Executive Summary

我们希望研究Undaria中岩藻多糖的产量如何受温度和时间水平的影响，以及这些因素是否相互作用。

研究发现，温度对产量的影响随时间变化而变化，因此我们无法单独考察温度和时间的影响。

在60度的温度下，预计在第2个时间点的产量比第4个时间点高出1到25单位。同样的结论也适用于70度的温度。

有证据表明，在60度的温度下，第2个时间点的产量高于80度的温度。

Additional Comments

从交互图来看，两个较低温度下的HiKda值分布几乎没有差异。将这两个组合并为一个组可能更有意义，因为这可以将fTemp简化为一个两水平因素，增加自由度并减少多重比较调整的幅度，从而提高统计功效。这是需要与研究人员讨论的问题。

Chapter 13: Modelling count data using the Poisson distribution（使用 Poisson 分布对计数数据进行建模）

1.计数数据的本质

定义： 计数数据是记录某个事件发生次数的变量，其值只能是非负整数 (0, 1, 2, 3, ...)。它是一种离散型变量。

本章关注类型： 主要关注事件独立发生且理论上没有明确上限的事件计数。

示例：

市场营销活动后购买次数的变化。
流行病学中每日新增感染人数。
运营研究中每日客户互动次数。
生态学中栖息地恢复前后动物数量。
口腔健康研究中受试者蛀牙数量。

线性回归的局限性： 尽管有时线性回归可用于分析计数数据（尤其是在对数转换后），但这通常不合适，因为计数数据通常不满足正态分布和等方差的假设，且对数转换无法处理0计数。

2.泊松分布 (Poisson Distribution)

适用场景： 常用于描述在固定空间或时间内随机发生的独立事件的计数。

特性：

取值为非负整数 {0, 1, 2, ...}，无上限。
由单一参数$ μ$ (均值) 决定，记为$ Pois(μ)$。
概率质量函数： $P (Y = y) = \frac{e^{- μ} μ^{y}}{y!}$ ，其中 y! 是 y 的阶乘。
均值与方差相等： $E (Y) = V a r (Y) = μ$ 。
当 μ 较小时，分布呈右偏；当 μ 较大时，分布近似正态分布（离散形式）。

R函数：

dpois(y, mu): 计算泊松分布的概率 $P (Y = y)$ 。
rpois(n, mu): 生成n个来自 $P o i s (μ)$ 分布的随机数。

独立性假设的重要性： 泊松分布适用于事件独立发生的情况。例如，地震灾害索赔数量可能不适合泊松分布，因为一次大地震可能引发多次索赔，事件不独立。

广义线性模型 (Generalized Linear Model, GLM)

引入原因： 计数数据通常不满足线性模型的正态性假设，需要更合适的模型。GLM通过允许响应变量服从其他分布（如泊松分布）并将线性预测变量通过连接函数与响应变量的期望联系起来，从而推广了标准线性模型。

泊松回归模型：

假设响应变量 Y 服从泊松分布： $Y \sim P o i s s o n (μ)$ 。
期望 $μ$ (即 $E [Y]$ ) 通过对数连接函数 (log link) 与解释变量 x 的线性组合相关联： $l o g (μ) = β_{0} + β_{1} x$ 。或者等价地： $μ = e x p (β_{0} + β_{1} x)$

这种形式确保了预测的均值 μ 始终为正。

模型参数估计通常使用最大似然法 (Maximum Likelihood Estimation)。

R函数： 使用 glm() 函数拟合。

# glm(formula, family = poisson, data = your_data)

4.过离散 (Overdispersion) 与准（准/拟）泊松模型 (Quasi-Poisson)

过离散： 当观测数据的方差远大于其均值时 (Var(Y)>E(Y))，就发生了过离散。这违反了泊松分布中均值等于方差的假设。

检验过离散：

查看残差离散度 (Residual Deviance) 与残差自由度 (Residual Degrees of Freedom)。如果残差离散度远大于其自由度 (通常看残差离散度 / 残差自由度是否远大于1)，则可能存在过离散。
更正式地，可以计算p值：1 - pchisq(residual_deviance, residual_df)。如果p值很小 (如 < 0.05)，则表明模型不充分，可能存在过离散。

准（拟，quasi）泊松模型：

当存在过离散时，可以使用拟泊松模型进行修正。它不假定特定的方差形式，而是估计一个离散参数 (dispersion parameter, $ϕ$ )，使得 $V a r (Y) = ϕ E (Y)$ （也就是原来 $V a r (Y) = E (Y)$ 现在就让 $V a r (Y) = k E (Y)$ 解决过离散问题）。
在R中，通过将 family = poisson 修改为 family = quasipoisson 来拟合。

glm(formula, family = quasipoisson, data = your_data)
拟泊松模型会调整参数估计的标准误，从而影响置信区间和p值，使得推断更为保守和稳健。系数估计值本身通常不变。

5.模型解释与推断

系数解释：

在对数连接的泊松回归中，解释变量 x 每增加一个单位，响应变量的期望均值 μ 会乘以 $e x p (β_{1})$ 。
$e x p (β_{1})$ 称为发生率比 (Rate Ratio) 或相对风险。
如果 $e x p (β_{1}) > 1$ ，表示 x 增加时，μ 增加。
如果 $e x p (β_{1}) < 1$ ，表示 x 增加时，μ 减少。
如果 $e x p (β_{1}) = 1$ ，表示 x 对 μ 没有影响。

置信区间： 对系数 β1 计算置信区间后，对其端点取指数 ( $e x p ()$ )，得到发生率比的置信区间。

预测：

predict(model, newdata, type = "link")：在对数尺度上（即 $β_{0} + β_{1} x$ ）进行预测。
predict(model, newdata, type = "response")：在原始尺度上（即 $μ = e x p (β_{0} + β_{1} x)$ ）进行预测，得到期望计数。
predictGLM() (s20x包) 可以方便地给出响应尺度上的预测值和置信区间。

例题分析：R包提交数量增长 (CRAN Submissions)

总览： 本例旨在分析自2005年至2016年，每年提交到CRAN (Comprehensive R Archive Network) 的R软件包数量 (Number) 的增长趋势，其中年份 (Year) 作为解释变量。

变量类型与转换：

响应（因）变量：Number (每年提交的R包数量，计数型)。
解释（自）变量：Year (年份，数值型)。

探索性数据分析：

绘制 Number vs Year 的散点图，发现原始尺度上关系呈指数增长。
绘制 log(Number) vs Year 的散点图，关系近似线性。这提示了对数转换或对数连接函数的适用性。

par(mfrow = c(1,2))

plot(Number ~ Year, data = CRAN.df)

plot(log(Number) ~ Year, data = CRAN.df)

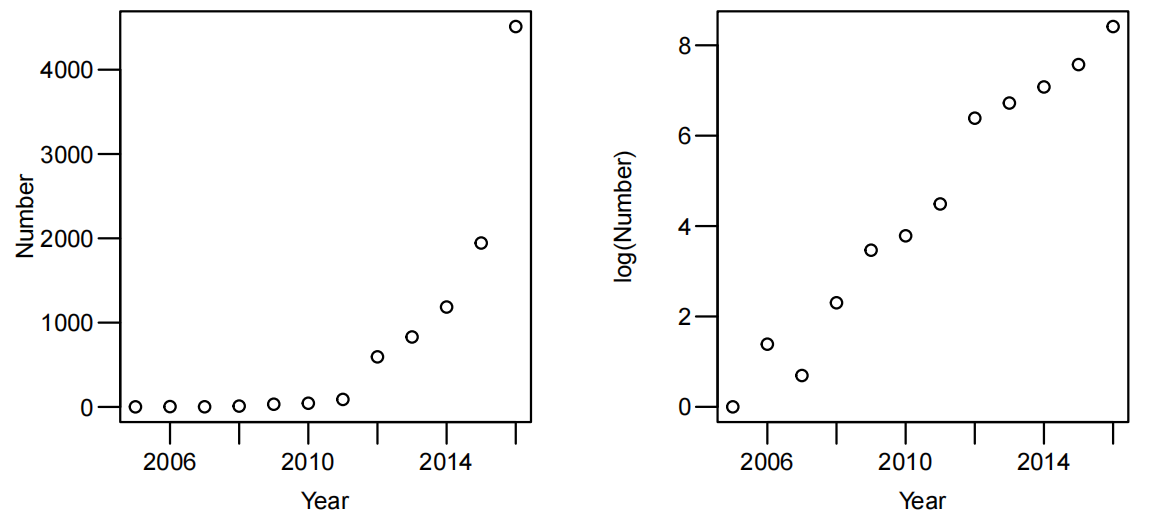
模型拟合与简化 (及比较)：

基于lm的对数转换模型 (作为对比)： 首先尝试用线性模型拟合对数转换后的响应变量。

CRAN.fit <- lm(log(Number) ~ Year, data = CRAN.df)

summary(CRAN.fit)

plot(CRAN.fit, which = 1) # 残差图

cooks20x(CRAN.fit) # Cook's 距离

模型诊断显示基本满足假设，但这种方法预测的是中位数，且无法处理0计数。

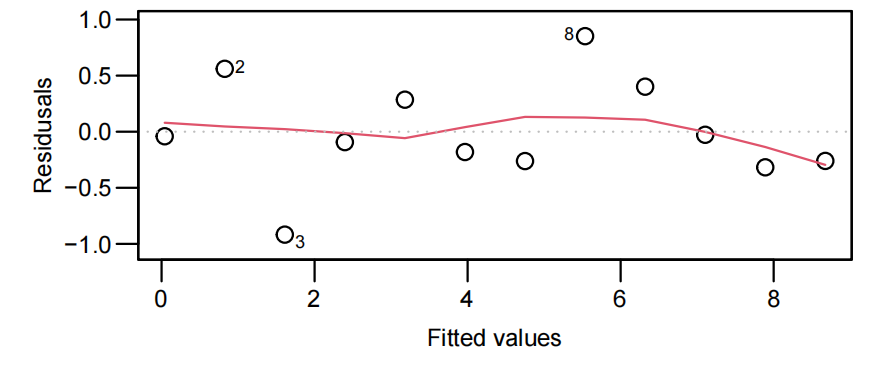
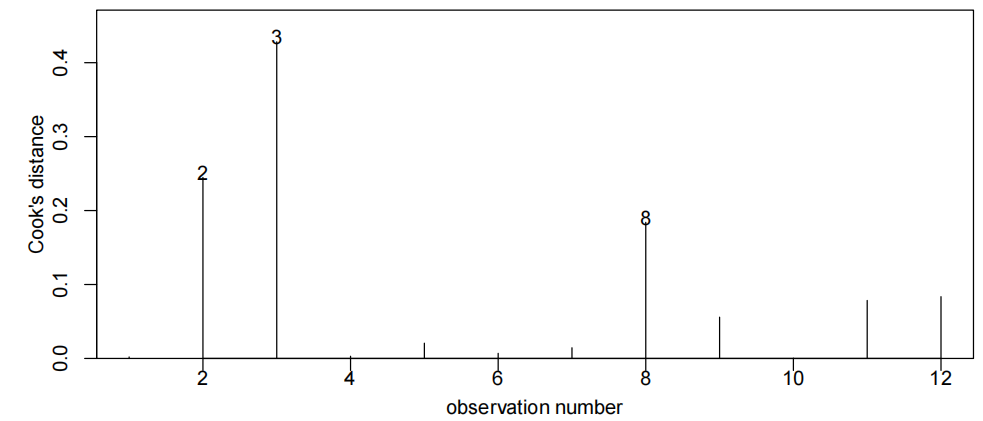
（观察点3的库克距离超过了我们的阈值0.4。然而，只有12次观测，这也许不是什么大问题。）

基于glm的泊松回归模型： 使用 glm 和 family = poisson 拟合。

CRAN.gfit <- glm(Number ~ Year, family = poisson, data = CRAN.df)

summary(CRAN.gfit)

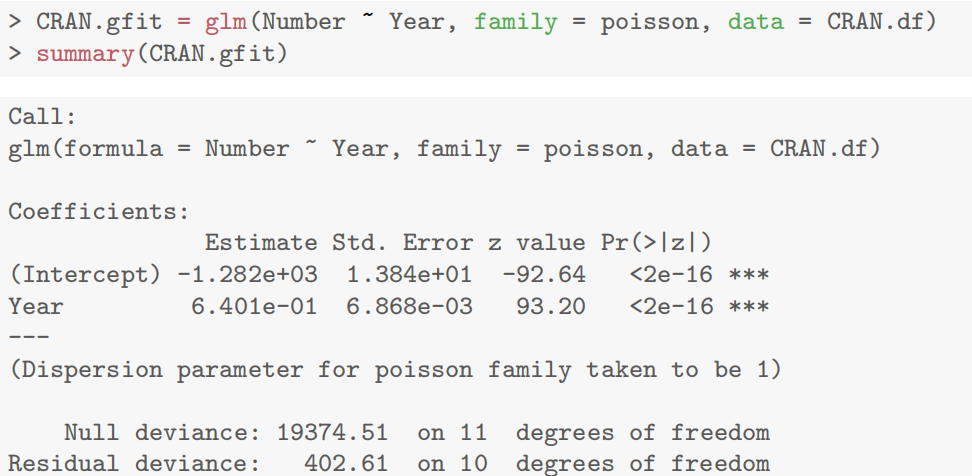
检验过离散：（其中1-pchisq这一步必须完成）

查看残差离散度 (Residual Deviance) 与残差自由度 (Residual Degrees of Freedom)。如果残差离散度远大于其自由度 (通常看残差离散度 / 残差自由度是否远大于1)，则可能存在过离散。

更正式地，可以计算p值：1 - pchisq(residual_deviance, residual_df)。如果p值很小 (如 < 0.05)，则表明模型不充分，可能存在过离散。

泊松模型诊断 (检查过离散)：

plot(CRAN.gfit, which = 1) # 残差图，注意其含义与lm不同

CRAN.gfit$deviance # 残差离散度

CRAN.gfit$df.residual # 残差自由度

1 - pchisq(CRAN.gfit$deviance, CRAN.gfit$df.residual) # 检验p值

教材中发现残差离散度 (402.61) 远大于自由度 (10)，p值接近0，表明存在严重的过离散，泊松模型不适用。

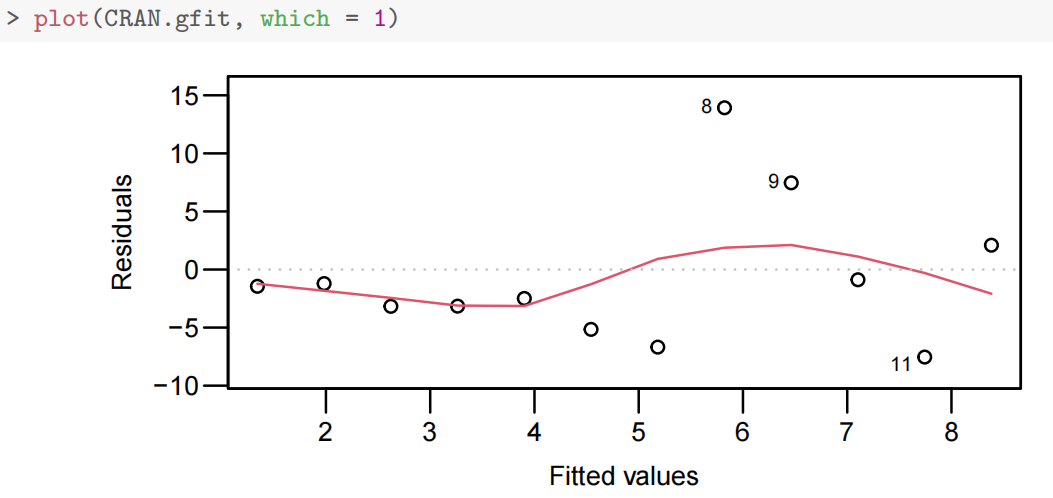
> 1 - pchisq(402.61,10)

[1] 0

基于glm的拟泊松回归模型： 因存在过离散，改用 family = quasipoisson。

CRAN.quasigfit <- glm(Number ~ Year, family = quasipoisson, data = CRAN.df)

summary(CRAN.quasigfit)

系数估计值与泊松模型相同，但标准误增大，t值 (summary中显示为t值而非z值) 减小，p值增大。离散参数 (Dispersion parameter) 估计为约41.26。

下图是glm-possion的：

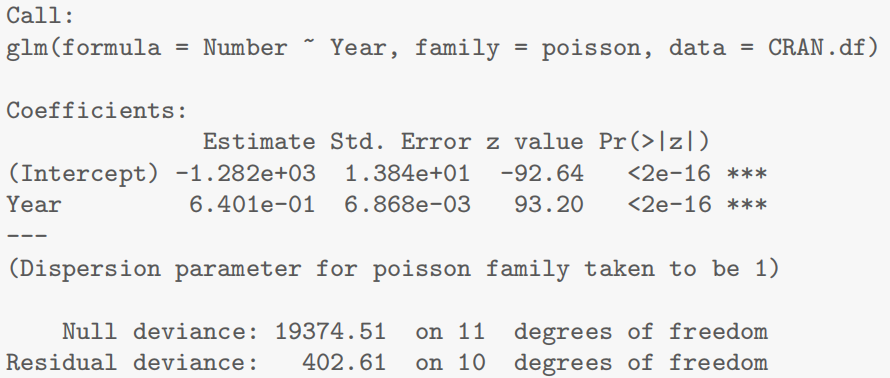
下图是glm-quasipossion的：

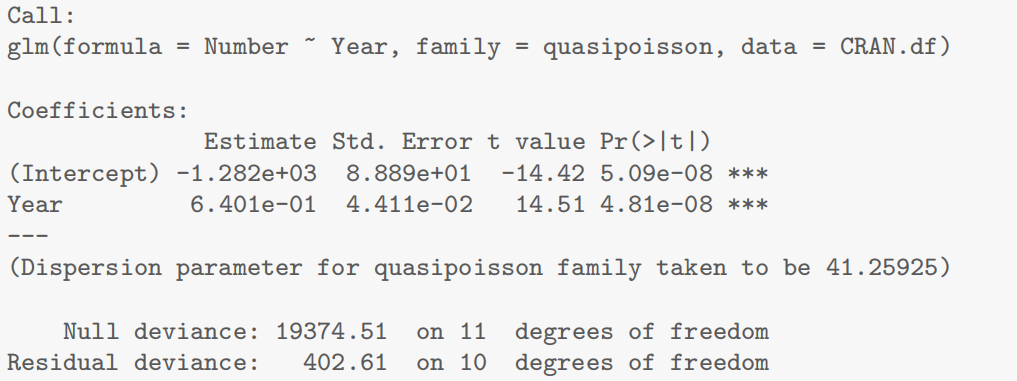
拟泊松模型诊断 (影响点)：

plot(CRAN.quasigfit, which = 4) # Cook's 距离图

教材指出，对于泊松回归，期望计数较大的观测点本身就具有较大影响，Cook's距离的解释需谨慎。

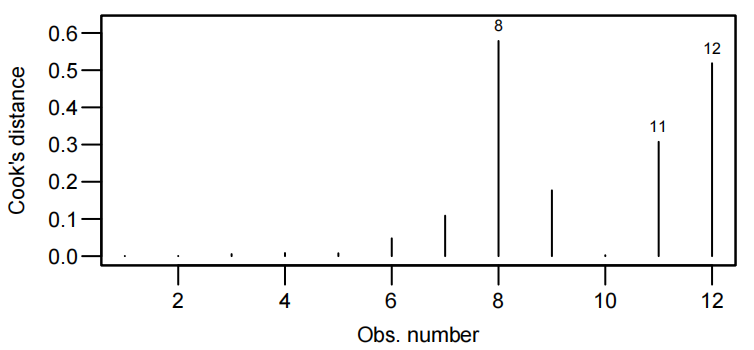
结果解释 (基于拟泊松模型 CRAN.quasigfit 和 95% 置信区间)：

年份的效应： Year 的系数估计值 (在对数尺度上) 为 β^1≈0.6401。年增长乘数 (发生率比) 为 exp(β^1)≈exp(0.6401)≈1.8966。其95%置信区间 (通过 exp(confint(CRAN.quasigfit)) 得到) 为 (1.7458, 2.0758) 或使用 confint.default 得到 (1.7395, 2.0679)。解释：每年CRAN提交的R包期望数量是前一年的1.75到2.08倍 (或1.74到2.07倍)，即每年增长75%到108% (或74%到107%)。
预测2017年的提交数量： 使用 predictGLM(CRAN.quasigfit, newdata = data.frame(Year = 2017), type = "response") 预测的期望提交数量为8294.82，95%置信区间为 (6626.62, 10382.97)。解释：预计2017年CRAN的R包提交数量在6600到10400之间。

GLM与LM(log-transformed)的比较：

GLM直接对原始计数建模，解释的是均值；LM(log-transformed)对转换后的数据建模，解释的是中位数。
GLM能更好地处理计数数据的方差随均值变化的特性。
GLM对0计数没有问题；LM(log-transformed)无法处理log(0)。
GLM在影响点分析上可能更合理，因为它允许高计数值有更大影响。
GLM的置信区间通常更窄。

第十三章R语言代码总结

1.如果响应变量（response）是计数变量（count）就建议使用GLM-Possion分布进行建模

CRAN.gfit= glm(Number~Year,family=poisson,data=CRAN.df)

summary(CRAN.gfit)

2.需要使用plot(CRAN.gfit,which=1)，cooks20x也可以用（较大的计数自然会比较小的计数更具影响力。）。但是不能使用normcheck检验正态：因为计数变量没有，glm通过某种手段（类似于插值拟合）使本用不了lm的计数变量能够用起来，因此无法normcheck

3.检验Possion模型是否过离散（算出来的值为p值，如果小于0.06就用准泊松模型quasipossion）

1-qchisq(CRAN.gfit$deviance.CRAN.gfit$df.residual)

4.准泊松模型（quasipossion）

CRAN.quasigfit<-glm(Number~Year,family=quasipossion,data=CRAN.df)

5.用exp将变量的影响转换回/解释为平均值或预期值的乘法变化

exp(confint(CRAN.quasigfit))

6.用predictGLM估计预期值的 95% 置信区间

待补全

7*.手动计算predictGLM的值

pred_link <- predict(CRAN.quasigfit, newdata = predCRAN.df, se.fit = TRUE)

lower_link <- pred_link$fit - 1.96 * pred_link$se.fit

upper_link <- pred_link$fit + 1.96 * pred_link$se.fit

pred_response_ci <- exp(c(fit = pred_link$fit, lwr = lower_link, upr = upper_link))

print(pred_response_ci)

Chapter 14: Poisson modelling of count data: Two examples（针对GLM-Poisson的两个例题）

例题1：地震频率 (Earthquake Frequency)

总览： 本例旨在研究地震震级 (Magnitude，数值型) 和地点 (Locn，因子型：南加州SC/华盛顿州WA) 如何影响地震发生的预期频率 (Freq，计数型)。特别关注地震频率随震级增加而下降的速率在两个地点是否相同 (即是否存在交互效应)。

背景知识：古登堡-里克特定律 (Gutenberg-Richter law) 描述了地震频率随震级增加而指数下降的关系，形式为$ log_{10}N=a−bM $，这可以转换为泊松回归中常见的$ μ=exp(β_0+β_1x)$形式。

变量类型与转换

响应变量：Freq (在特定震级范围内的地震发生次数，计数型)。

解释变量：

Magnitude (震级，数值型)。
Locn (地点，分类变量)，需转换为因子 (levels: SC, WA)。

探索性数据分析

绘制 Freq vs Magnitude 的散点图，并用不同符号区分地点。

plot(Freq ~ Magnitude, data = Quakes.df, pch = substr(Locn, 1, 1))

图中数据点大致呈指数衰减趋势，初步观察两个地点的衰减速率可能不同。

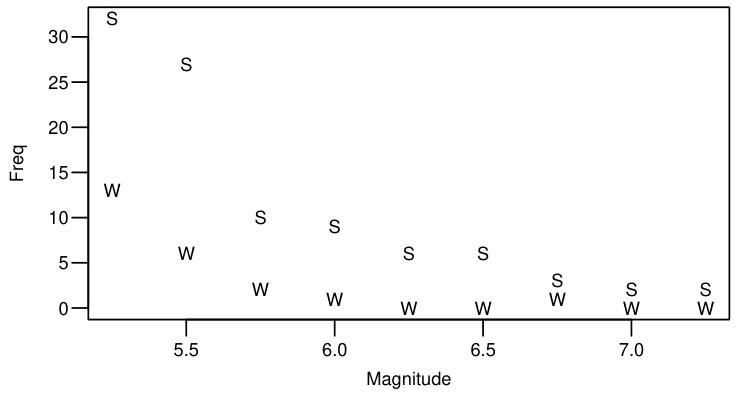
模型拟合与简化

拟合含交互项的泊松回归模型： 由于有两个解释变量 (一个数值型，一个因子型)，我们首先拟合包含它们主效应以及交互效应 (Locn:Magnitude) 的模型。

Quake.gfit <- glm(Freq ~ Locn * Magnitude, family = poisson, data = Quakes.df)

# Locn * Magnitude 等价于 Locn + Magnitude + Locn:Magnitude

模型诊断 (泊松模型)：

残差图：plot(Quake.gfit, which = 1)。教材认为图形可接受。

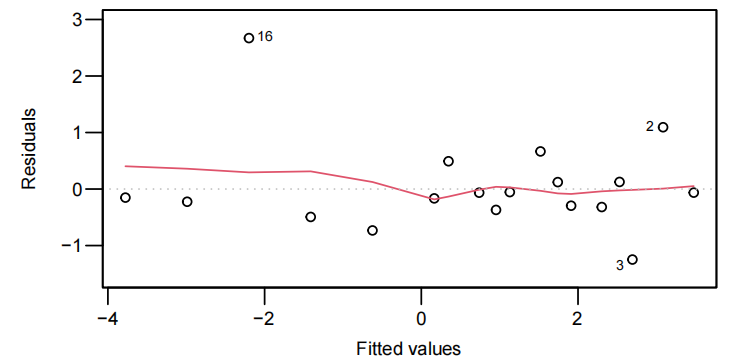
影响点：plot(Quake.gfit, which = 4) (Cook's距离)。无特别大的影响点。

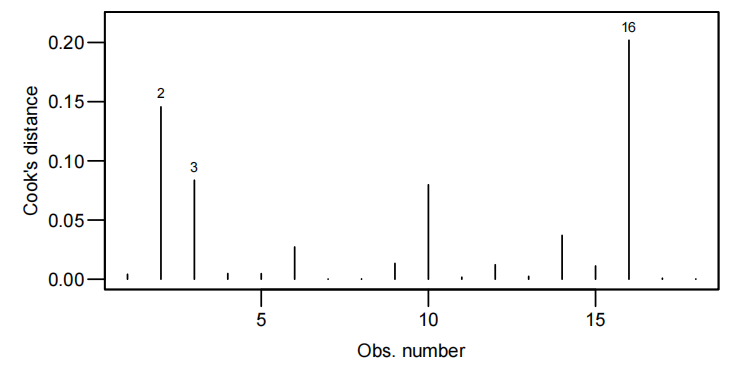
过离散检验：

summary(Quake.gfit) # 查看残差离散度和自由度

看的是Residual deviance和自由度的大小，可以发现8.2295<14，基本可以判定没有过离散

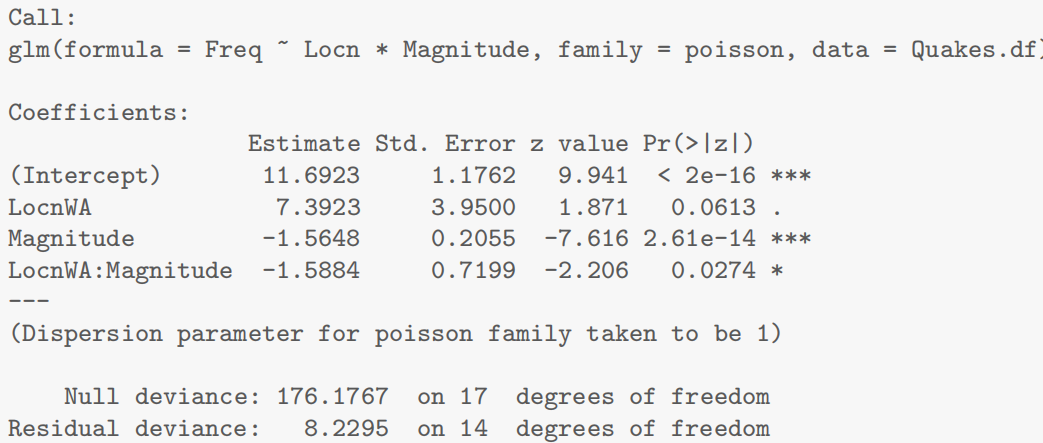
1 - pchisq(Quake.gfit$deviance, Quake.gfit$df.residual)

R 语言中的pchisq()函数对应的英文单词是 "Probability Chi-Square"，表示卡方分布的累积概率函数。

> 1 - pchisq(8.23, 14)

[1] 0.8770025

p值为0.877，远大于0.05，表明没有过离散问题，泊松模型适用。

检验交互项的显著性

查看 summary(Quake.gfit) 中交互项 LocnWA:Magnitude (假设SC为基线) 的p值。教材中此p值为0.0274<0.05，说明还是有影响的。

模型确定

由于交互项的p值 (0.0274) 小于0.05，交互效应显著。这意味着震级对地震频率的影响在南加州和华盛顿州是不同的。因此，最终模型应保留交互项，即 Quake.gfit。

结果解释 (基于 Quake.gfit 和 95% 置信区间)

Quake.cis = confint(Quake.gfit)

exp(Quake.cis[3,])

100*(1-exp(Quake.cis[3,]))

南加州 (SC - 基线组) 中震级的影响： Magnitude 的系数 β^Mag 估计了SC地区震级每增加1单位，log(期望频率)的变化。 exp(β^Mag) 是频率的乘数效应。教材中，SC地区 (Magnitude的系数) 的95%置信区间取指数后为 (0.1375, 0.3082)。解释：在南加州，震级每增加1个单位，预期的地震频率将乘以0.1375到0.3082倍，即预期频率下降约69.2%到86.3% (100×(1−0.3082) 到 100×(1−0.1375))。

华盛顿州 (WA) 中震级的影响： 为了直接得到WA地区震级的影响，需要更改Locn的基线水平为"WA"，然后重新拟合模型，或者从交互模型中计算。

uakes.df$Locn2 <- relevel(Quakes.df$Locn, ref = "WA")

Quake2.gfit <- glm(Freq ~ Locn2 * Magnitude, family = poisson, data = Quakes.df)

exp(confint(Quake2.gfit)["Magnitude", ]) # 获取WA地区Magnitude效应的CI

教材中，WA地区震级效应的95%置信区间取指数后为 (0.00908, 0.14018)。解释：在华盛顿州，震级每增加1个单位，预期的地震频率将乘以0.00908到0.14018倍，即预期频率下降约86.0%到99.1%。

结论： 地震频率随震级增加的下降速率在华盛顿州比在南加州更快。

例题2：鲷鱼计数 (Snapper Counts)

（只需掌握模型拟合与简化及后面部分即可）

总览： 本例研究地点 (Locn，因子型：Leigh/Hahei) 和保护区状态 (Reserve，因子型：Yes/No) 如何影响通过水下诱饵摄像机 (BUV) 观察到的鲷鱼数量 (Freq，计数型)。

变量类型与转换：

响应变量：Freq (观察到的鲷鱼数量，计数型)。
解释变量：

Locn (地点)，转换为因子 (levels: Hahei, Leigh)。

Reserve (是否为保护区)，转换为因子 (levels: N, Y)。

Snap.df <- read.table("Data/SnapperCROPvsHAHEI.txt", header = TRUE)

探索性数据分析： 使用 interactionPlots() (s20x包) 绘制交互图。

interactionPlots(Freq ~ Locn + Reserve, data = Snap.df)

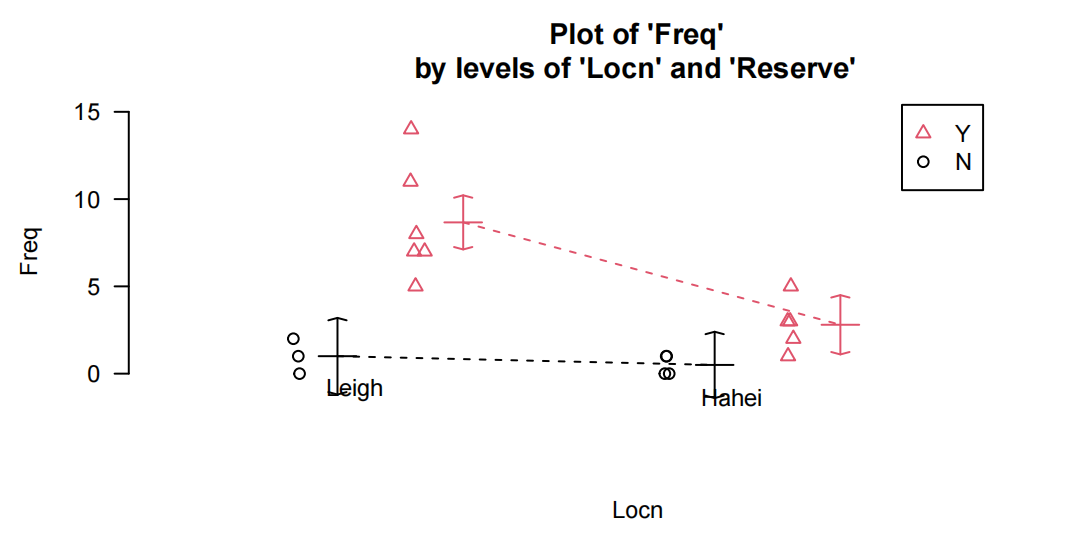
教材提示：对于GLM，交互图中的平行线并不直接对应于无交互效应（因为连接函数是非线性的），但仍可作为初步观察。

模型拟合与简化

拟合含交互项的泊松回归模型

Snap.glm<-glm(Freq~Locn*Reverse,family=Possion,data=Snap.df)

模型诊断 (泊松模型)

残差图：plot(Snap.glm, which = 1)。图形可接受。

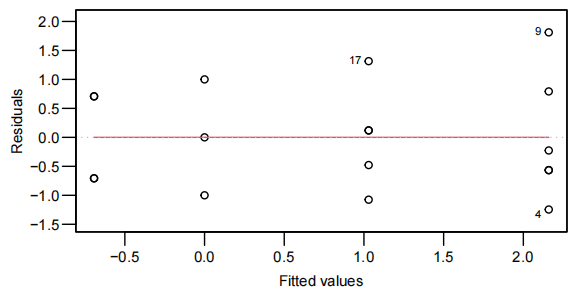
影响点：plot(Snap.glm, which = 4)。无特别大的影响点。

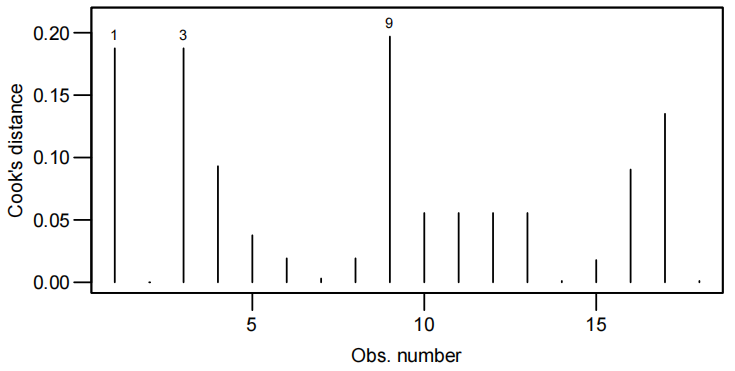
过离散检验：

summary(Snap.glm)

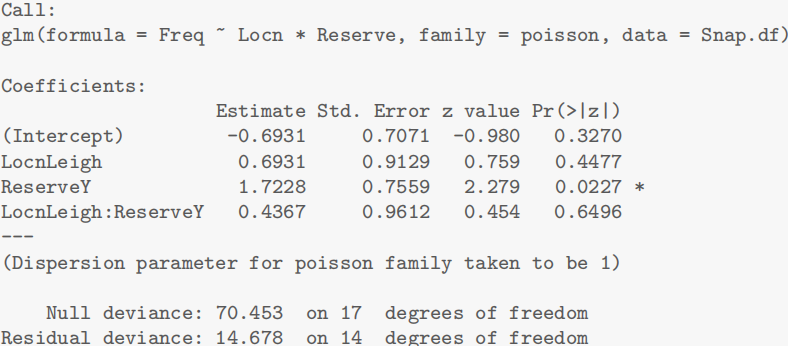
1-pchisq(Sanp.glm$deviance,Snap.glm$df.residual)

即1-pchisq(14.678,14)

R 语言中的pchisq()函数对应的英文单词是 "Probability Chi-Square"，表示卡方分布的累积概率函数。

> 1 - pchisq(14.678, 14)

[1] 0.4005141

教材中残差离散度 (14.678) 与自由度 (14) 相近，p值为0.4005，表明没有过离散。泊松模型适用。

检验交互项的显著性

查看 summary(Snap.glm) 中交互项 LocnLeigh:ReserveY (假设Hahei和N为基线) 的p值。教材中此p值为0.6496>0.05，因此没有显著交互效应。

模型简化决策 (移除交互项)

由于交互项的p值 (0.6496) 远大于0.05，交互效应不显著。简化模型，移除交互项。

Snap2.gfit<-glm(Freq~Lcon+Reverse,family=Possion,data=Snap.df)

summary(Snap2.fit)

1-pchisq(14.879,15)

> 1 - pchisq(14.879, 15)

[1] 0.4601677

summary(Snap2.glm) 显示 LocnLeigh (p ≈ 0.000128) 和 ReserveY (p ≈ 1.51e-05) 的主效应均高度显著。过离散检验 (对主效应模型)：残差离散度14.879，自由度15，p值0.460，仍然表明无过离散。

模型确定

最终模型为只包含主效应的 Snap2.glm。

结果解释 (基于 Snap2.glm 和 95% 置信区间)

Snap.cis <- exp(confint(Snap2.glm))

cis: cofidence intervals

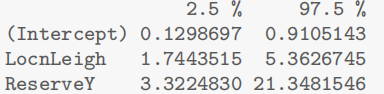
保护区状态 (Reserve) 的效应： ReserveY 的系数指数化后的95%置信区间为 (3.322, 21.348)。解释：控制地点因素后，在海洋保护区内观察到的鲷鱼期望数量是在保护区外的3.3到21.3倍。
地点 (Locn) 的效应： LocnLeigh 的系数指数化后的95%置信区间为 (1.744, 5.363)。解释：控制保护区状态后，在Leigh地点观察到的鲷鱼期望数量是在Hahei地点的1.7到5.4倍。

补充（感觉不理解也没关系）：使用 anova() 进行联合假设检验 (GLM中)

当需要检验一个包含多个水平的因子或多个参数的联合显著性时，可以使用 anova() 函数，推荐使用 test = "Chisq" (或 test = "LRT" for Likelihood Ratio Test)。

anova(Snap2.glm, test = "Chisq")

这会给出每个项加入模型时离散度减少的显著性。

Case Study 14.1: Decline in expected earthquake numbers with magnitude

Problem

古登堡-里克特定律指出，地震的预期频率随其震级成倍减少。公式为$ log_{10}N=a−bM$，其中N是里氏震级M或以上的地震的预期次数，a和b为未知参数。

在应用了健康的微积分之后，这个公式可以被重新表达成一个对我们来说更熟悉的形式： $E [Y | x] = e x p (β_{0} + β_{1} x)$ ，其中，Y是震级在x−δ和x + δ之间的地震次数。（在上面的公式中，β0和β1以一种复杂的方式依赖于a、b和δ，我们不会关心这一点。）

关注的变量为：

•强度：记录到的地震的强度。

•地点：描述地震位置的二级因素。–它有两个级别，南加州（“SC”）和华盛顿州（“WA”）。

•频率：在地点记录到的、具有该强度的地震数量。

Question of Interest

研究问题是量化加州和华盛顿州地震频率（随着震级的增加）下降的速度，并评估这些速度是否相同。

Read in and Inspect the Data

Quakes.df=read.table("EarthquakeMagnitudes.txt",header=T)

Quakes.df$Locn=as.factor(Quakes$Locn)

Quakes.df

## Locn Magnitude Freq

## 1 SC 5.25 32

## 2 SC 5.50 27

## 3 SC 5.75 10

## 4 SC 6.00 9

## 5 SC 6.25 6

## 6 SC 6.50 6

## 7 SC 6.75 3

## 8 SC 7.00 2

## 9 SC 7.25 2

## 10 WA 5.25 13

## 11 WA 5.50 6

## 12 WA 5.75 2

## 13 WA 6.00 1

## 14 WA 6.25 0

## 15 WA 6.50 0

## 16 WA 6.75 1

## 17 WA 7.00 0

## 18 WA 7.25 0

plot(Freq ~ Magnitude, data = Quakes.df, pch = substr(Locn, 1, 1))

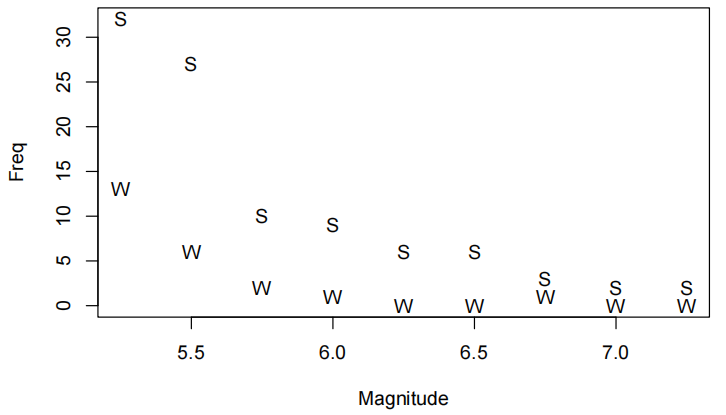
曲线与频率和幅度之间的指数关系一致，尚不清楚两个位置的衰减倍数是否相同。

Model Building and Check Assumptions

Quake.fit=glm(Freq~Locn*Magnitude,family=Possion,data=Quakes.df)

plot(Quake.gfit,which=1,pch=substr(Quakes.df$Locn,1,1)

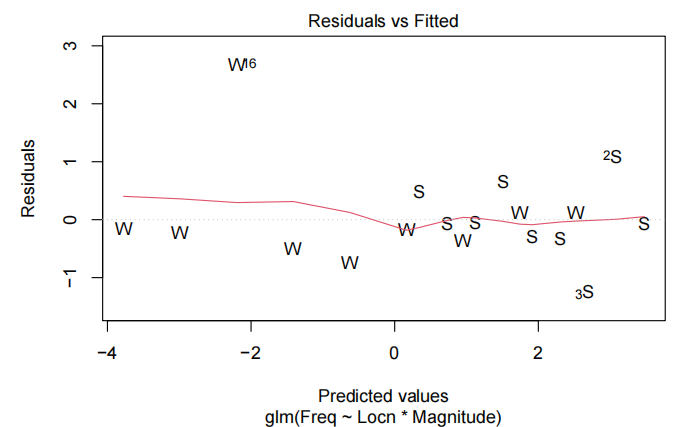
cooks20x(Quake.gfit)/plot(Quake.gfit,which=4)

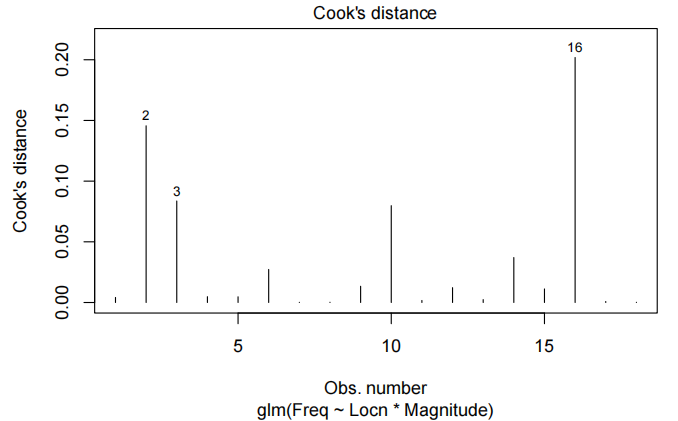
观察值16的残差较大，但由于该观测值的拟合值µ非常小，因此可以忽略。

summary(Quake.gfit)

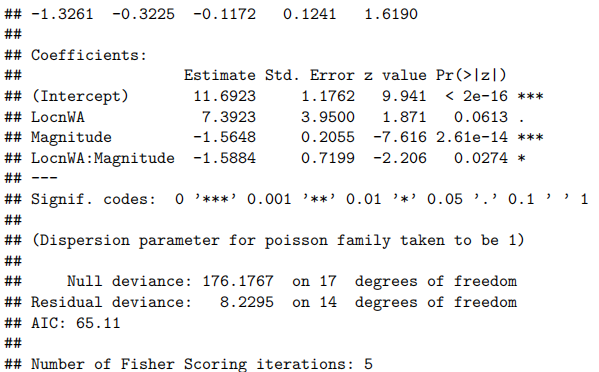
1-pchisq(8.2295,14)

## [1] 0.8770025

exp(confint(Quake.gfit)[3, ])

# Multiplicative annual change in CA/CA的年乘数变化

## Waiting for profiling to be done...

## 2.5 % 97.5 %

## 0.1374743 0.3082437

100 * (1 - exp(confint(Quake.gfit)[3, ]))

# Percentage annual decrease in CA

## Waiting for profiling to be done...

## 2.5 % 97.5 %

## 86.25257 69.17563

Additional Output with WA as the baseline Level

Quakes.df$Locn = relevel(Quakes.df$Locn, ref = "WA")

Quake2.gfit = glm(Freq ~ Locn * Magnitude, family = poisson, data = Quakes.df)

exp(confint(Quake2.gfit)[3, ]) # Multiplicative annual change in WA

## Waiting for profiling to be done...

## 2.5 % 97.5 %

## 0.009077661 0.140175445

100 * (1 - exp(confint(Quake2.gfit)[3, ])) # Percentage annual decrease in WA

## Waiting for profiling to be done...

## 2.5 % 97.5 %

## 99.09223 85.98246

Methods and Assumption Checks

由于响应变量（response variable）地震频率是一个计数（count），我们拟合了一个具有泊松响应分布（Possion response distribution）的广义（generalized）线性模型。我们有两个解释变量（explanatory variable）：震级（数值）和位置（分类）。震级与频率的散点图（scatterplot）显示了两个地点都呈指数递减趋势。拟合了一个包含震级与位置交互作用的泊松模型。结果显示震级与位置之间的交互作用显著（interaction between……and……is significant）（P值≈0.03)。

所有模型假设均得到满足。我们可以信任该模型的结果。

我们的最终模型是：

$l o g (μ_{i}) = β_{0} + β_{1} \times L o c n . W A_{i} + β_{2} \times M a g n i t u d e_{i} + β_{3} \times L o c n . W A_{i} \times M a g n i t u d e_{i}$

其中 $µ_{i}$ 是震级为 $i$ 的地震平均次数（mean number）（GLM都描述为均值）， $L o c n . W A_{i}$ 等于1表示地震发生在华盛顿，否则为0。地震次数（在位置Locn.W ai处震级为M）服从均值为 $µ_{i}$ 的泊松分布。

Executive Summary

研究问题在于量化（quantify）加利福尼亚州和华盛顿州地震频率（随震级增加）下降的速度，并评估这些速度是否相同。

在华盛顿州，地震频率（随震级增加）的下降速度比加利福尼亚州更快。

在华盛顿州，地震预期数量每增加一个里氏震级，会减少86.0%到99.0%。（描述confint结果）

而在加利福尼亚州，这一下降幅度则在69.2%到86.3%之间。（描述confint结果）

Case Study 14.2: Snapper counts in and around marine reserves

Problem

水下诱饵视频（BUV）是计数鱼类如红鲷鱼的常用工具。

BUV在两个地点使用，分别是莱伊和哈希。每个地点都有一个海洋保护区。BUV在保护区内的地点以及保护区外的地点进行了部署。总共在18个地点使用了BUV。

感兴趣的变量包括：

•地点：一个两层因素，描述了BUV的位置。–具有“莱伊”和“哈希”两个等级。•预保护区：一个两层因素，描述了BUV是否位于海洋保护区。–具有“否”和“是”两个等级。

•频率：由BUV统计的捕获数量。

Question of Interest

探索有关位置和预订状态的梭鱼数量相对情况很有意义。

Read in and Inspect the Data

Snap.df=read.table("SnapperCROPvsHAHEI.txt", header = T)

interactionPlots(Freq~Locn*Reverse,data=Snap.df,col.width=0)

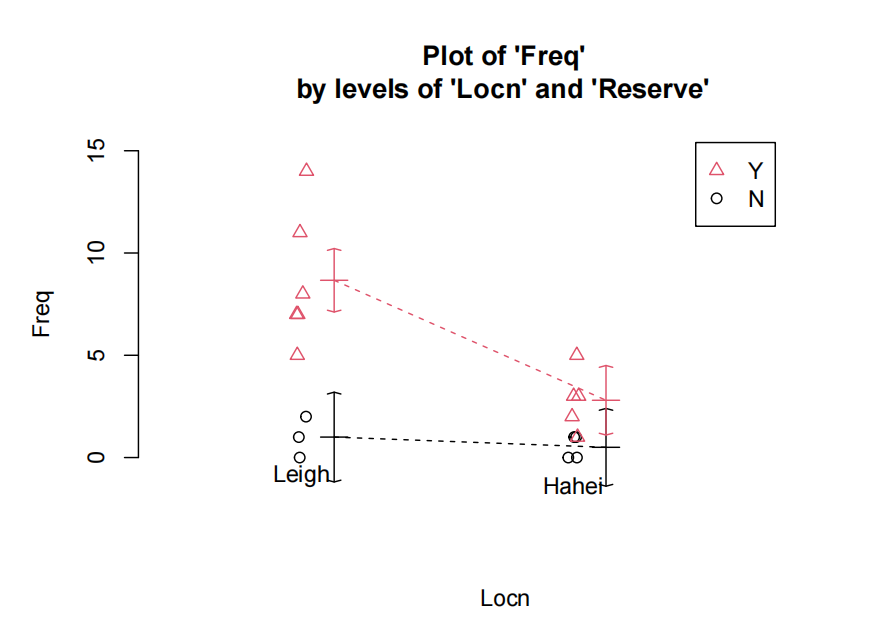
在莱伊，海洋保护区内的鲷鱼数量似乎比非保护区更高。而在哈希，海洋保护区内的鲷鱼数量与非保护区相比几乎没有差异。然而，交互图显示，在这两个地点，保护区的乘数效应可能是相似的（即没有交互作用）。

Model Building and Check Assumptions

Snap.glm<-glm(Freq~Locn*Reserve,family=Possion,data=Snap.df)

summary(Snap.glm)

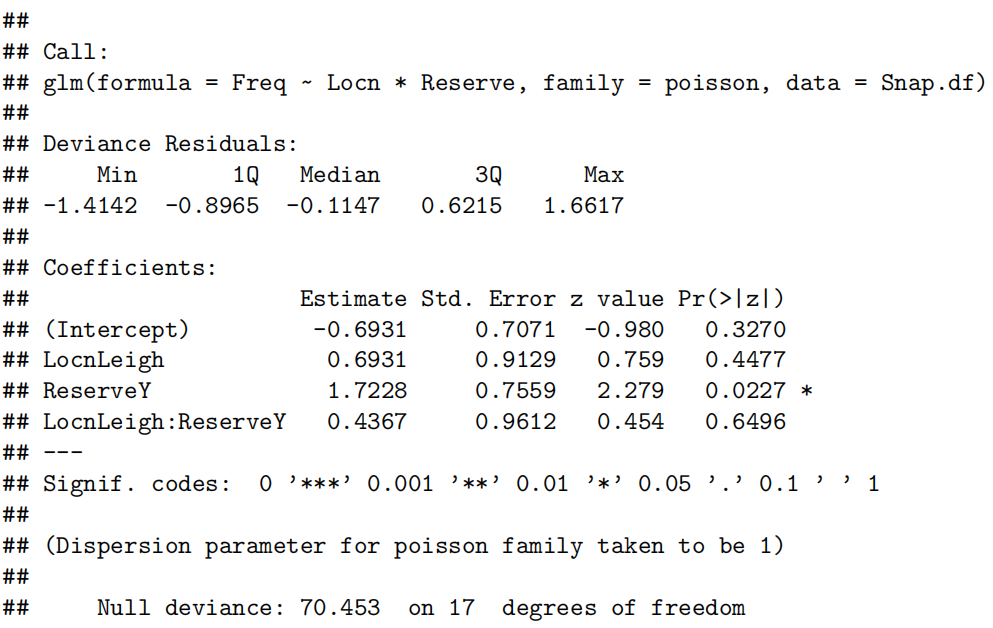
## Residual deviance: 14.678 on 14 degrees of freedom

## AIC: 69.143

## Number of Fisher Scoring iterations: 5

1-pchisq(14.678,14)

## [1] 0.4005141

Snap2.glm<-glm(Freq~Locn+Reserve,family=possion,data=Snap.df)

summary(Snap2.glm)

plot(Snap2.glm,which=1)

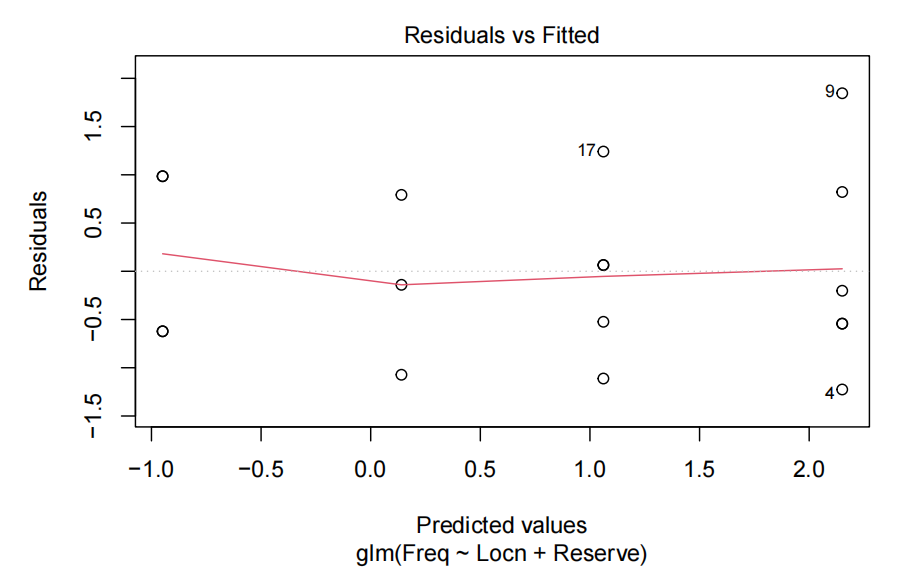
exp(confint(Snap2.glm))

Methods and Assumption Checks

作为响应变量，Freq是一个计数，我们拟合了一个具有泊松响应分布的广义线性模型。我们有两个解释因素：Locn和Reserve。最初，我们在Reserve和location之间拟合了交互作用项。交互作用项不显著（P值= 0.65)，因此模型仅保留主效应进行了重新拟合。两个因素都显著，因此最终模型中保留了这两个因素。

所有假设均得到满足。没有证据表明过度离散，因此我们可以信任泊松模型的结果（P值= 0.40)。

对于我们的最终模型，我们假设观察i的捕捞量是均值µi的泊松分布，其中

$l o g (μ_{i}) = β_{0} + β_{1} \times L o c n . L e i g h_{i} + β_{2} \times R e v e r s e . Y e s_{i}$

其中，Locn.Leighi和Reserve.Yesi是虚拟变量，如果观察值i分别来自Leigh和海洋保护区，则取值为1，否则取值为0。

Executive Summary

探索红鲷鱼的数量与地理位置及保护区状态之间的关系十分有趣。

我们得出结论，在海洋保护区内的红鲷鱼数量预期是保护区外的3到21倍。

此外，莱伊地区的红鲷鱼数量预期是哈黑地区的1.7到5.4倍。

Chapter 15: Modelling proportion data using the binomial distribution（用二项式分布对比例数据进行建模）

二元 (伯努利) 数据、优势比 (Odds) 与对数优势比 (Log-odds)

1.二元 (伯努利) 数据 (Binary/Bernoulli Data)

响应变量只有两种可能结果，通常编码为 0 (失败/否) 或 1 (成功/是)。
一次试验的结果服从伯努利分布，其参数为 p (成功的概率)。
均值 $E [Y] = p$ ，方差 $V a r (Y) = p (1 - p)$ 。

2.优势比 (Odds):

事件发生的概率与不发生的概率之比：

$O d d s = \frac{P (事件不发生)}{P (事件发生)} = \frac{p}{1 - p}$
优势比的范围是 $[0, \infty)$ 。
如果知道优势比，可以计算概率： $p = \frac{O d d s}{1 + O d d s} = \frac{\frac{p}{1 - p}}{1 + \frac{p}{1 - p}} = \frac{\frac{p}{1 - p}}{\frac{1 - p + p}{1 - p}} = p$

3.对数优势比 (Log-odds / Logit):

优势比的自然对数：

$L o g - o d d s = l o g (O d d s) = l o g (\frac{p}{1 - p}) \equiv l o g i t (p)$
对数优势比的范围是 (−∞,+∞)，这使其适合作为线性模型的响应。
如果知道对数优势比，可以计算概率：

$p=\frac{exp(Log-odds)}{1+exp(Log-odds)} $(这是逻辑斯谛函数，R中为 plogis())。

建模对数优势比 (logistic回归)

1.模型形式： 将对数优势比与解释变量的线性组合联系起来：

$l o g i t (p) = l o g (\frac{p}{1 - p}) = β_{0} + β_{1} x_{1} + β_{2} x_{2} + . . .$

对于单个数值型解释变量 x： $l o g (\frac{p}{1 - p} = β_{0} + β_{1} x)$

等价地，概率 p 的形式为：$p=\frac{exp(\beta_0+\beta_1x)}{1+exp(\beta_0+\beta_1x)}=\frac{e^{\beta_0+\beta_1x } } {1+e^{\beta_0+\beta_1x } } $

这个 p 关于 x 的函数呈 "S" 形曲线。

例如，如果 $β_{0} = - 10$ 且 $β_{1} = 0.3$ ，则曲线如下所示：

$β_{1}$ 的大小越大，曲线越陡。
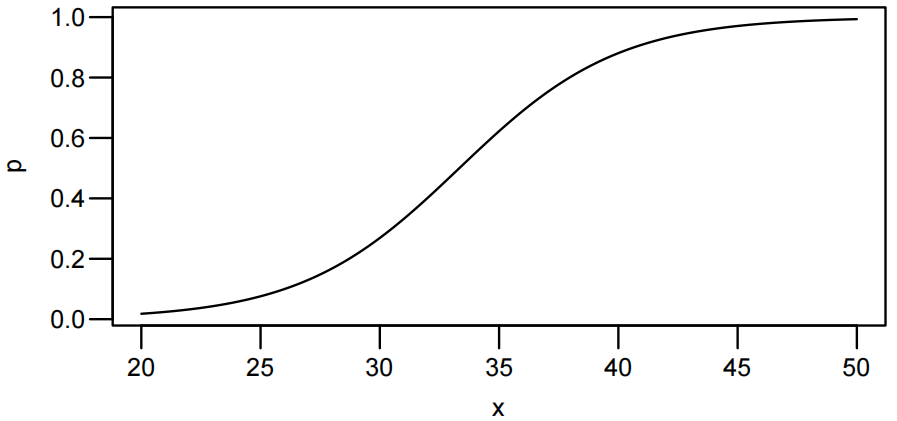
如果 $β_{1} < 0$ ，则曲线为反“S”形。
更改 $β_{0}$ 可以更改曲线的水平位置。

2.逻辑斯谛回归 (Logistic Regression)

这种使用logit作为连接函数，对二元或比例数据进行建模的方法称为逻辑斯谛回归。它是广义线性模型 (GLM) 的一种，响应变量服从二项分布 (伯努利分布是其特例)，连接函数是logit。

3.系数解释 ( $β_{1}$ )

当解释变量 $x$ 每增加一个单位时，对数优势比增加 $β_{1}$ 。

等价地，优势比乘以 $e x p (β_{1})$ 。$exp(β_1) $称为优势比率 (Odds Ratio, OR)。

如果 $e x p (β_{1}) > 1$ ，表示 x 增加时，成功的优势比增加。
如果 $e x p (β_{1}) < 1$ ，表示 x 增加时，成功的优势比减少。
如果 $e x p (β_{1}) = 1$ ，表示 x 对成功的优势比没有影响。

通过 glm 建模二元响应 (未分组数据)

适用情况： 数据中每一行代表一次独立的伯努利试验，响应变量为0或1。

R函数： 使用 glm() 函数，并设置 family = binomial (默认使用logit连接函数)。

model_fit<-glm(response~explanatory1+explanatory2,family=binomial,data=Data.df)

模型诊断： 对于未分组的二元数据，传统的残差图和影响点诊断通常信息量不大，因为残差本身也只有几个可能的值。通常假设模型满足基本条件。不能直接使用残差离散度来评估模型拟合好坏。

通过 glm 建模二项响应 (分组数据)

适用情况： 数据中每一行代表一组试验 (例如，n 次试验)，记录了成功次数 k (或成功比例 k/n) 以及相应的解释变量值。

R函数： 仍然使用 glm() 和 family = binomial。

model_gfit<-glm(proportion_success~predictor,weights=number_of_trials,family=binomial, data = grouped_data)

模型诊断 (分组数据)：

过离散 (Overdispersion)： 当观测数据的方差大于二项分布假设的方差时发生。
- 检验：查看残差离散度 (Residual Deviance) 与残差自由度 (Residual df)。如果残差离散度远大于残差自由度，或
 
 1 - pchisq(residual_deviance, residual_df) 的p值很小 ( < 0.05)，则可能存在过离散。
- 处理：如果存在过离散，应改用 family = quasibinomial 重新拟合模型。这将调整标准误和p值，但不改变系数估计。
残差图 (plot(model, which = 1)) 在分组数据且每组期望成功数和失败数都较大 (如 > 5) 时更有用。

模型解释与推断 (logistic回归)

系数解释： 如前所述，exp(βk) 表示对应解释变量 xk 每增加一个单位，成功优势比的乘性变化。

置信区间：

对系数 $β_{k}$ 计算置信区间。
对置信区间的端点取指数 (exp())，得到优势比率的置信区间。

预测概率 p：

predict(model, newdata, type = "link")：在对数优势比尺度上预测。
predict(model, newdata, type = "response")：直接预测概率 p。
predictGLM(model, newdata, type = "response") (s20x包)：预测概率 p 并给出其置信区间。

第十五章R语言代码总结

1.未分组数据（即0/1的二进制数据，稀疏数据sparse data）使用GLM-binomial拟合模型

bb.fit2<-glm(basket~distance,family=binomial,data=bb.df)

2.分组数据能够检查假设并决定是否使用family=quasibinomial

语法1-指定成功比例和试验次数

bb.fit3<-glm(propn~distance*gender,weight=n,family=binomial,data=bb.grouped.df)

语法2-指定成功和失败的频率

bb.grouped.df<-transform(bb.grouped.df,success=n*propn,fail=n*(1-propn))

bb.fit4<-glm(cbind(success,fail)~distance*gender,family=binomial,data=bb.grouped.df)

3.残差检验与GLM-Possion是一致的

1-pchisq(bb.fit4$deviance,bb.fit4$df.residual)

1-pchisq(2.3688,2)

如果算出来p-value<0.05就用family=quasibinomial

4.计算参数置信区间并用exp反转解释对几率的乘法效应（百分比变化）

exp(confint(bb.fit2))

5.预测概率的置信区间predictGLM，其中type="response"代表直接反映到概率，而type="link"就只管到odd也就是优势比

bb.pred.intervals<-predictGLM(bb.fit2,newdata=data.frame(distance=c(1,2,3)),type="response")

bb.pred.intervals

怎么理解100*(exp(cinfint(Haddock.glm))-1)的作用？

confint(Haddock.glm)

作用：获取逻辑回归模型 Haddock.glm 中各参数的置信区间（默认 95% 置信水平），结果在对数优势比（log-odds）尺度上。

背景：在拖网捕鱼案例中，Haddock.glm 模型拟合了鱼的叉长（fork length）与被保留概率的关系，参数估计值在对数优势比尺度上。

exp(confint(...))

作用：将对数优势比尺度的置信区间转换为优势比（Odds Ratio）尺度。

原理：若参数 (\beta) 表示对数优势比的变化，则 (\exp(\beta)) 表示优势比的倍数（如 (\exp(\beta)=1.4) 表示 odds 增加 40%）。

exp(...) - 1

作用：将优势比转换为优势比的变化量。

示例：若优势比为 1.4，则变化量为 (1.4 - 1 = 0.4)，即 odds 增加 40%。

100 \* (...)

作用：将变化量转换为百分比形式，便于直观解释。

结果解读：如输出 30% 表示 “自变量每变化 1 单位，事件发生的 odds 增加 30%”。

Case Study 15.1: Haddock retention in a trawl

Problem

实验包括观察在给定叉长下进入拖网鳕鱼笼的鱼的数量，以及被它保留的鱼的数量。

在Haddock.df数据框中，codend是保留的codend编号，cover是逃逸到覆盖区域的编号。因此，鱼类总数为codend + cover。

感兴趣的变量为：

•propn：拖网捕获的鱼的比例。

•forklen：鱼的叉长（以厘米计）。（这是从吻部到尾鳍末端的长度。）

Question of Interest

鱼的长度如何影响它被拖网捕获的几率？

Read in and Inspect the Data

Haddock.df<-read.table("Haddock.txt",headr=T)

Haddock.df$n<-with(Haddock.df,codend+cover)

Haddock.df$propn<-with(Haddock.df,codend/n)

plot(propn~forklen,data=Haddock.df,xlab="Fork length (cm)",las=1)

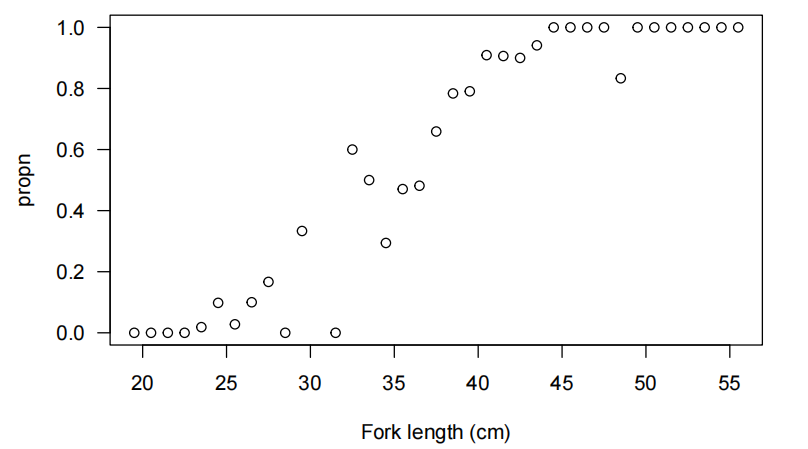
我们可以看到，随着鱼的长度增加，拖网捕获的鳕鱼比例也增加。值得注意的是，这一比例呈S形曲线。

Model Building and Check Assumptions

Haddock.glm<-glm(propn~forklen,family=binomial,weight=n,data=Haddock.df)

plot(Haddock,which=1)

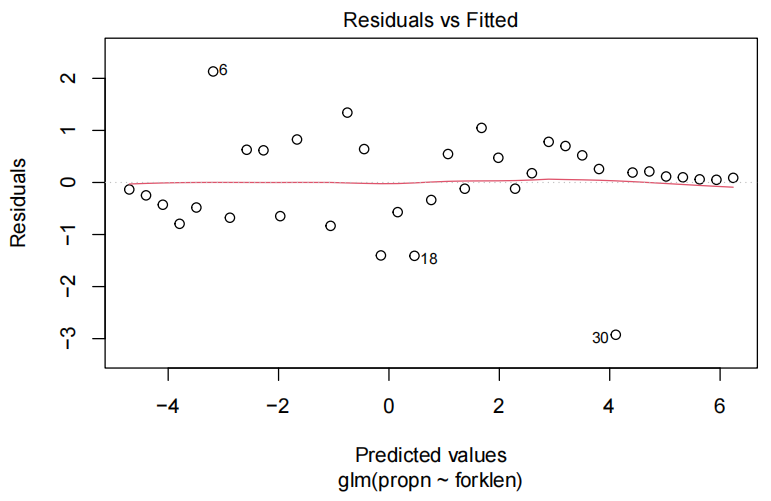
summary(Haddock.glm)

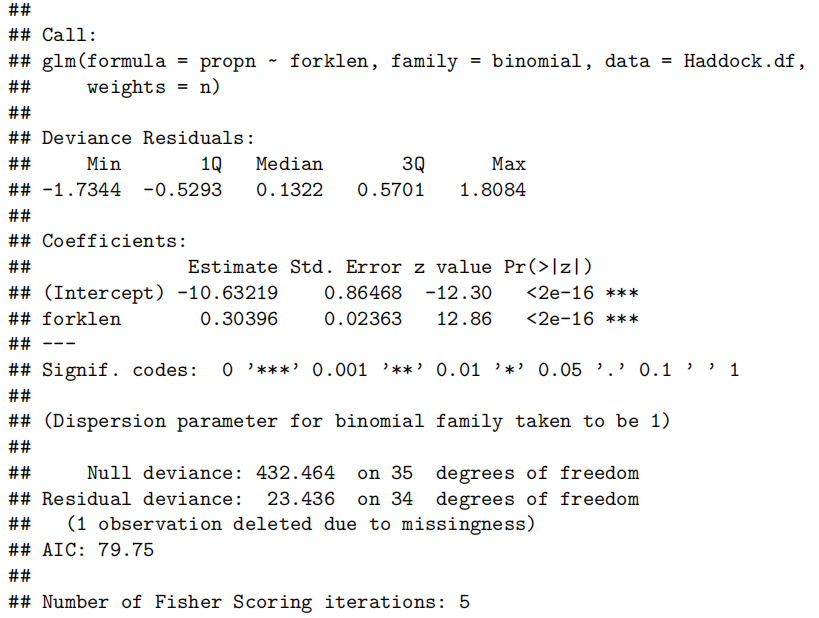
1-pchisq(23.436,34)

## [1] 0.9133009

exp(confint(Haddock.glm))

100*(exp(cinfint(Haddock.glm))-1)

Methods and assumption Checks

记录了进入鳕鱼网的鱼的数量以及被保留的鱼的数量，针对不同叉长的鱼类。因此，我们拟合了一个二项逻辑回归模型，其中叉长（数值）是唯一的预测变量。响应数据被视为分组数据，每个组对应一个特定的叉长值。

考虑到我们预期高保留概率长度类别的残差会很小，拟合二项式模型的残差图没有显示出明显的趋势。没有证据表明存在过度离散（P值= 0.91)，因此我们可以信任该二项式模型的结果。

我们最终模型是： $l o g (O d d s_{i}) = β_{0} + β_{1} \times l e n g t h_{i}$

其中 $O d d s i$ 是鱼在第i个叉长值处的保留几率。

Executive Summary

我们的目的是调查鱼叉长度与进入拖网鳕鱼笼后被保留的几率之间的关系。

我们估计，每增加1厘米的鳕鱼叉长，它被保留在鳕鱼尾部的可能性就会增加30%到42%。

Case Study 15.2: Whio chick surviva

Chapter 16: Analysis of contingency tables（列联表分析）

引言与分类数据

分类数据 (Categorical Data): 当对每个观测对象测量的所有变量都是因子变量时，数据即为分类数据。因子变量的水平即为类别。

列联表 (Contingency Table): 将分类数据中各个因子水平组合出现的频数（计数）排列成的表格。

双向表 (Two-way Table): 由两个因子变量交叉分类形成，如 r×c 表（r 个行水平，c 个列水平）。
多维表 (Multi-way Table): 由三个或更多因子变量交叉分类形成。

分析目的：主要研究因子变量之间是否存在关联 (association / independence)，如果存在关联，则量化其强度。

解释变量与响应变量： 在某些情况下，可以区分解释变量和响应变量（如疫苗研究中，处理是解释变量，反应程度是响应）；而在其他情况下（如头发颜色与眼睛颜色研究），这种区分可能不明确。

数据来源： 计数可能来自固定试验次数（类似二项数据）或不固定（类似泊松数据）。这种区分可能影响解释，但分析方法（GLM）通常可以通用。

二项模型分析列联表 (以2x2表示例)

适用思路： 当可以将一个因子视为解释变量，另一个二分因子视为响应结果（成功/失败）时，可以使用二项GLM。

数据准备： 将列联表转换为每行代表解释变量的一个水平，列包含成功次数和失败次数 (或总次数和成功比例)。

模型拟合：

Freqs.df<-data.frame(Attend=c("not.attend","attend"),Fail=c(27.17),Pass=c(19.83))

# 假设 Freqs.df 的结构如下：

# Attend Fail Pass

# not.attend 27 19

# attend 17 83

AP.binom<-glm(cbind(Pass,Fail)~Attend,data=Freqs.df,family=binomial)

结果解释： 解释变量的系数的指数形式 (exp(β1)) 表示该水平相对于基线水平，成功结果的优势比率。例如，在出勤/通过的例子中， $\exp ({\hat{β}}_{Attend})$ 表示出勤学生通过考试的优势比是不出勤学生通过考试优势比的倍数。

泊松模型分析列联表 (以2x2表示例)

适用思路： 将列联表中的每个单元格的频数视为一个泊松计数，其期望值受行因子、列因子及其交互作用的影响。

数据准备： 将列联表“拉长”，每行代表一个单元格，包含行因子水平、列因子水平以及对应的频数。

模型拟合 (交互模型)： 对于单元格 (i,j)（第 i 行，第 j 列），其期望频数 E[nij] 的模型为： $l o g (E [n i j]) = μ + α_{i} + γ_{j} + (α γ)_{i j}$

其中$ α_i $是行效应，$ γ_j $是列效应，$ (αγ)_{ij}$是交互效应。

# 假设 Freqs2.df 的结构如下 (长格式)：
# Attend     Pass      freq
# attend     fail      17
# attend     pass      83
# not.attend fail      27
# not.attend pass      19

Freqs2.df$Attend <- relevel(Freqs2.df$Attend, ref = "not.attend") # 设置基线

Freqs2.df$Pass <- relevel(Freqs2.df$Pass, ref = "fail") # 设置基线

AP.pois <- glm(freq ~ Attend * Pass, family = poisson, data = Freqs2.df)

结果解释 (交互项)： 在饱和模型 (参数个数等于单元格数) 中，交互项系数的指数形式 ( $e x p ({\hat{β}}_{i n t e r a c t i o n})$ ) 即为优势比率 (Odds Ratio, OR)。

对于一个2x2表：

| | 列 1 (Fail) | 列 2 (Pass) |
| ----------------- | ----------- | ----------- |
| 行 1 (Not Attend) | 27 | 19 |
| 行 2 (Attend) | 17 | 83 |

如果基线是行1和列1，则交互项 Attend_attend:Pass_pass 的系数 β3 的指数形式 exp(β3) 等于 (n11n22)/(n12n21)。这表示行2中列2对列1的优势比，与行1中列2对列1的优势比之比。

二项与泊松模型的等价性 (特指2x2饱和模型)

对于2x2列联表，当使用二项GLM分析一个变量对另一个二元变量的效应时，得到的对数优势比估计，与使用饱和泊松GLM分析这两个变量的关联时，交互项的对数优势比率估计在数值上是相同的。

这意味着两种方法在这种特定情况下可以得出关于优势比的相同推断（点估计和置信区间）。

饱和模型 (Saturated Model): 指模型中待估参数的数量等于数据中独立单元格的数量。这样的模型总能完美拟合数据，其残差离散度（Residual Deviance）为0，自由度也为0。

泊松模型的优势

通用性强：

二项模型主要适用于响应变量是二分（或可以转化为二分比例）的情况。
泊松模型（对数线性模型）非常灵活，可以分析任意维度的列联表（例如 r×c 表，三维表等）。
它可以用来检验更复杂的独立性假设（例如，在三维表中检验条件独立性或所有双向交互作用）。

因此，在列联表分析中，基于泊松分布的对数线性模型是一种更通用和强大的工具。

优势比率 (Odds Ratio, OR) (可选内容)

定义 (2x2表)： 对于一个2x2表：

| | 结果 B1 | 结果 B2 |
| ----- | ------- | ------- |
| 组 A1 | n11 | n12 |
| 组 A2 | n21 | n22 |

组 $A_{1}$ 中结果 $B_{2}$ 对 $B_{1}$ 的优势比为 $n_{12} / n_{11}$ 。组 $A_{2}$ 中结果 $B_{2}$ 对 $B_{1}$ 的优势比为 $n_{22} / n_{21}$ 。优势比率 (OR) 是这两个优势比的比值： $OR=\frac{n_{12}/n_{11 } } {n_{22}/n_{21 } } =\frac{n_{12}n_{21 } } {n_{11}n_{22 } } $

解释：

OR=1: 组别A与结果B之间无关联。
OR>1: 组A2发生结果B2的优势相对于B1的优势，要高于组A1。
OR<1: 组A2发生结果B2的优势相对于B1的优势，要低于组A1。

推断： 通常在对数尺度上进行推断，因为 log(OR) 的抽样分布更接近正态分布。其标准误的近似公式为：

$S E (l o g (\hat{O R})) \approx \sqrt{\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + \frac{1}{n_{22}}}$

置信区间先在对数尺度计算，然后取指数转换回OR尺度。

卡方检验 (Chi-squared Test for Association) (可选内容)

目的： 检验列联表中行变量和列变量之间是否存在统计学上的关联（即是否独立）。

原假设 ( $H_{0}$ )：行变量与列变量相互独立（无关联）。

备择假设 ( $H_{1}$ )：行变量与列变量不独立（有关联）。

检验统计量：

$X^2=\sum\sum\frac{(O_{ij}−E_{ij})^2}{E_{ij } } $

其中 $O_{i j}$ 是单元格 (i,j) 的观测频数， $E_{i j}$ 是在 H0 为真时单元格 (i,j) 的期望频数。期望频数计算公式为：

$E_{i j} = \frac{总样本量}{(第 i 行的总和) \times (第 j 列的总和)}$

分布： 在 H0 为真且样本量足够大（通常要求所有期望频数 Eij≥5）的条件下，X2 近似服从自由度为 (r−1)(c−1) 的卡方分布。

R函数： chisq.test(table_object, correct = FALSE) (当不使用Yates连续性校正时)。

与GLM的关系： 对于r×c表，卡方检验的独立性假设等价于对数线性模型中交互项为零的假设。

Case Study 16.1: Gender bias in admissions to Berkeley

Problem

加州大学伯克利分校因1973年录取4526名申请研究生项目的学生时存在性别偏见而被起诉。

感兴趣的变量包括：

部门：六级分类变量，级别为‘A’、‘B’、‘C’、‘D’和‘E’。
性别：二分类变量，级别为‘F’和‘M’。
结果：二分类变量，级别为‘入’和‘出’。
频率：计数变量，对应于部门、性别和结果的观察组合。

Question of Interest

我们想要研究性别与入院结果之间的关系。

Read in and naive analysis

Berk.df<-read.table("BerkeleyEnrolments.txt",header=T)

head(Berk.df)

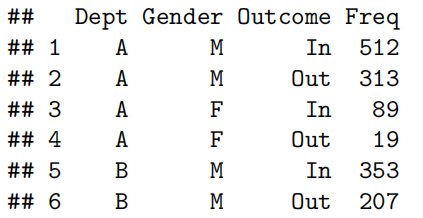
Berk.df<-transform(Berk.df,Dept=favtor(Dept),Gender=factor(Gender),Outcome=factor(Outcome))

Berk.tbl<-xtabs(Freq~Gender+Outcome,data=Berk.df)

Berk.tbl

## Outcome

## Gender In Out

## F 557 1278

## M 1198 1493

barplot(t(Berk.tbl),main="Berkeley admissions by

gender",col=c("lightblue","lightgreen"),xlab="gender",legend.text=c("In","Out))

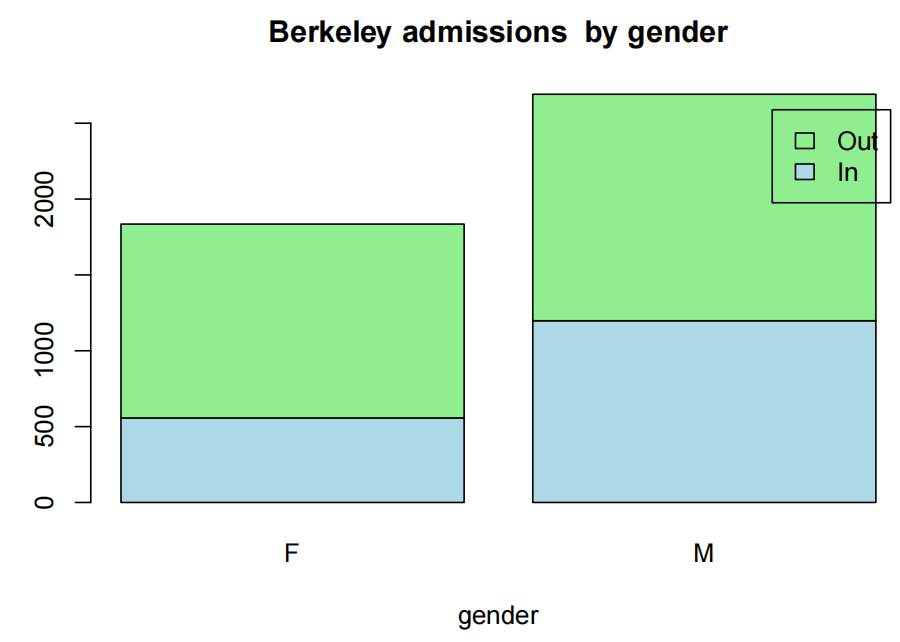
#Berk.gfit0 = glm(Freq ~ Gender \* Outcome,family = poisson, data = Berk.df)

#The above fit is over-dispersed, so quasi fit used*

Berk.quasifit0 = glm(Freq ~ Gender * Outcome,family = quasipoisson, data = Berk.df)

coef(summary(Berk.quasifit0))

exp(confint(Berk.quasifit0))[4,] #女性被排除在伯克利之外的几率！！

这似乎表明了一个明显的性别歧视案例——律师们高兴地搓着手。

然而，我们需要注意。在统计学330课程（这是本课程的后续课程）中，我们了解到，关联并不等同于因果关系。在这个案例中，性别与结果之间存在显著的关联，但这并不能直接证明两者之间存在因果联系。

在统计学330课程中，我们会进一步探讨是否存在间接的因果路径。实际上，我们想要探究的是：“如果其他条件相同，除了性别之外，女性和男性的几率是否相同？”这意味着我们需要考虑申请同一部门的男性和女性之间的差异。

考虑到部门因素会使模型变得更加复杂。拟合包含三向交互作用的模型无法提供有意义的解释，因此决定仅拟合包含所有双向交互作用的模型：

Model Building and Check Assumptions

Berk.gfit<-glm(Freq~Dept*Gender+Dept*Outcome+Gender*Outcome,family=possion,data=Berk.df)

plot(Berk.gfit,which=1)

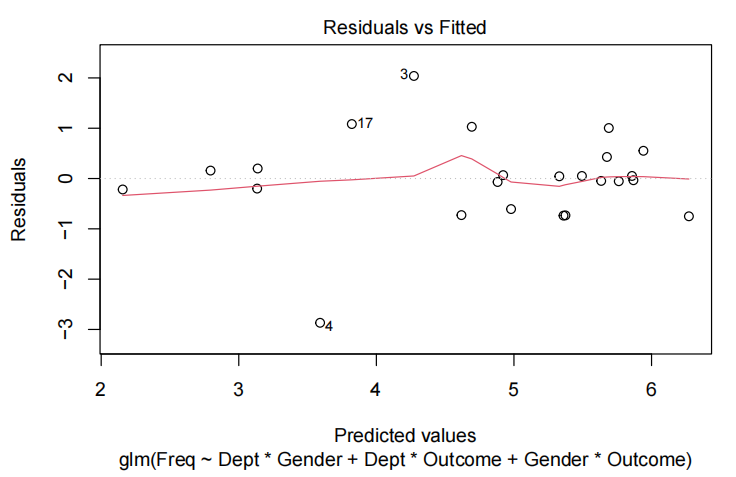
#接下来的两个调用是为了减少anova产生的输出量

Berk.gfit.anova<-anova(Berk.gfit,test="Chisq")

Berk.gfit.anova[,names(Berk.gfit.anova)]

summary(Berk.gfit)

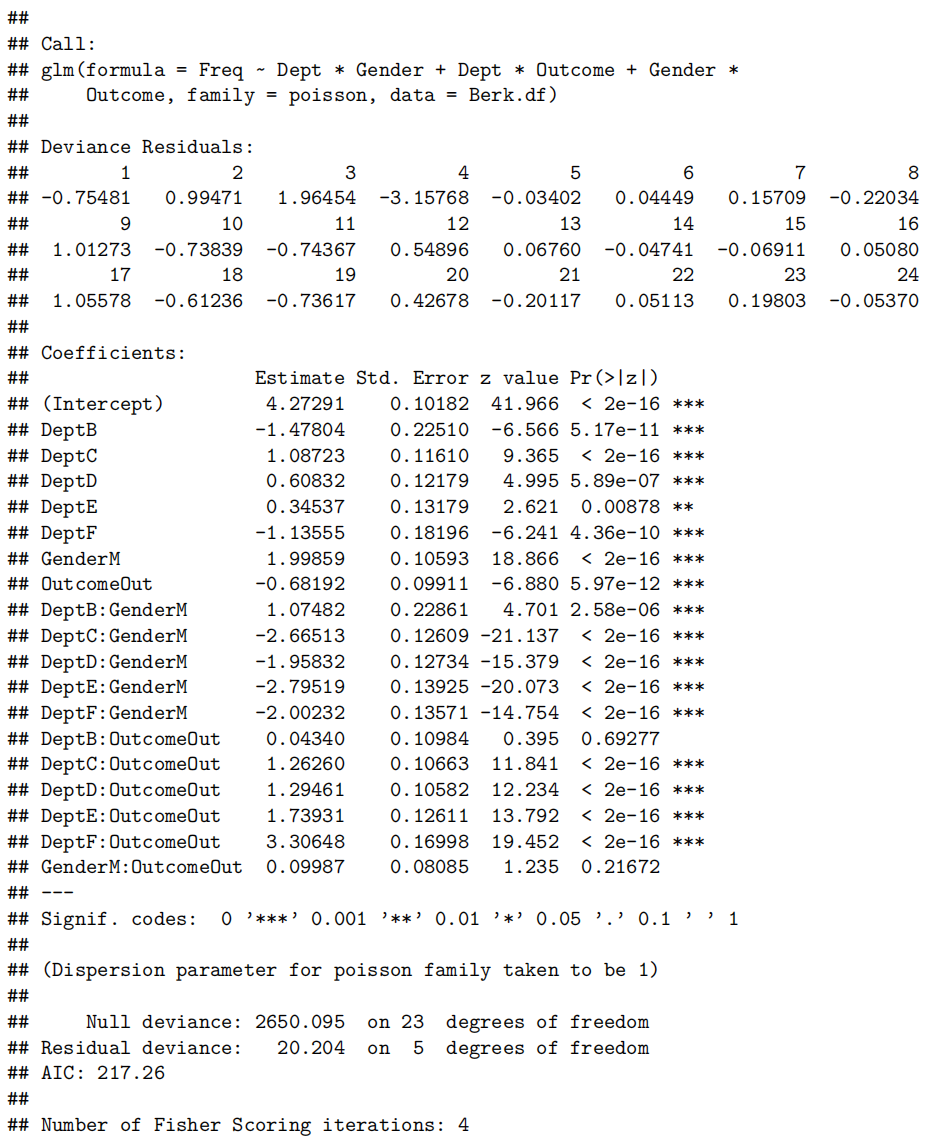
1-pchisq(20.204,5)（<0.05要用quasi）

## [1] 0.001144215

Berk.quasigfit<-glm(Freq~Dept*Gender+Dept*Outcome+Gender*Outcome,family=quasipossion)

Berk.quasigfit.anova<-anova(Berk.quasigfit,test="F")

Berk.quasigfit.anova[,names(Berk.quasigfit.anova)]

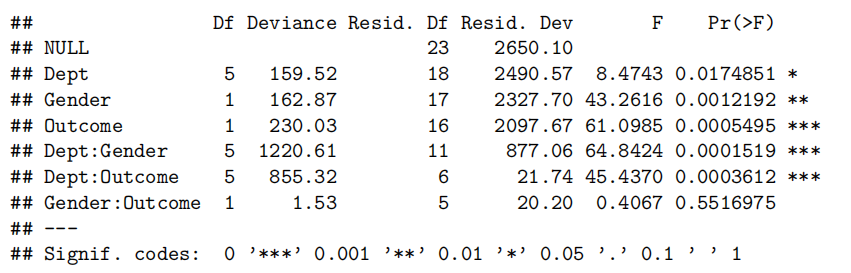
summary(Berk.quasigfit)

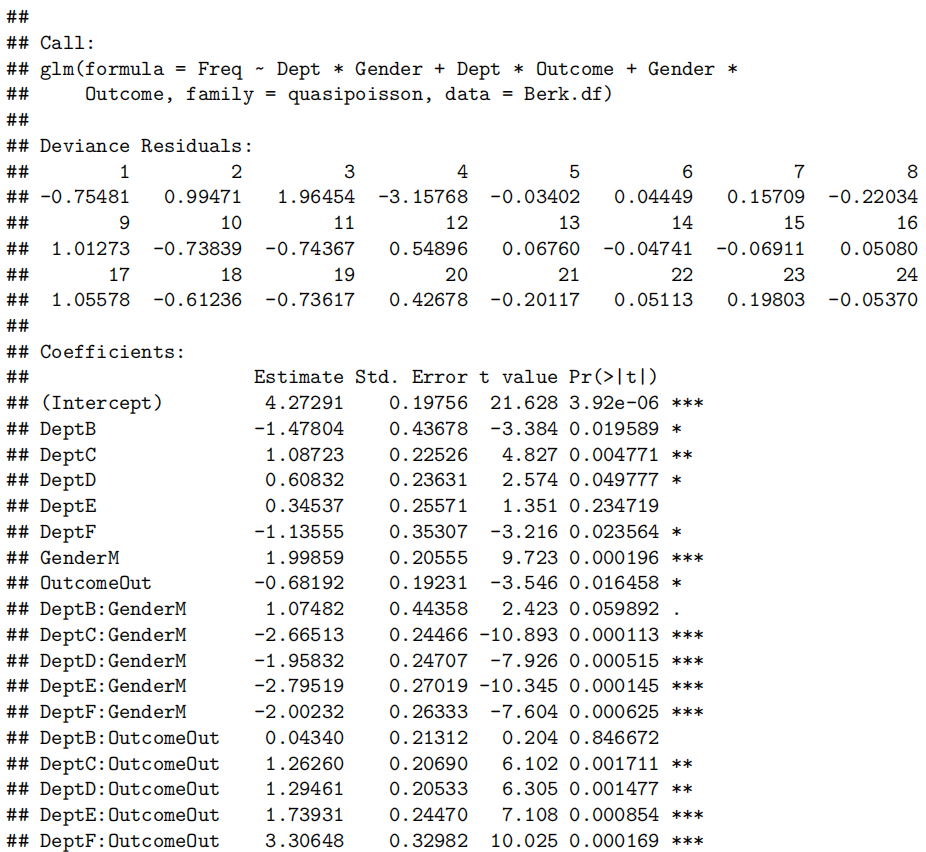
Produce the Additional Output Required

# Before adjusting for individual departments

chisq.test(Berk.tbl, correct = FALSE)

##

## Pearson’s Chi-squared test

##

## data: Berk.tbl

## X-squared = 92.205, df = 1, p-value < 2.2e-16

# After adjusting for individual departments

Berk.summ = coef(summary(Berk.quasigfit))

Berk.summ[nrow(Berk.summ), ]

## Estimate Std. Error t value Pr(>|t|)

## 0.09987009 0.15686847 0.63664858 0.55235491

c(exp(Berk.summ[nrow(Berk.summ), 1]), exp(confint(Berk.quasigfit)[nrow(Berk.summ), ]))

Method and Assumption Checks

我们的响应变量是按性别、结果和部门三个解释因素分解的计数。由于我们希望在其他条件相同的情况下评估性别的影响，因此拟合了一个广义线性三因素方差分析模型，该模型包括所有可能的两因素交互项。通过按部门查看数据，我们强烈预期某些与部门相关的二阶交互项将会显著。

残差图显示没有明显的趋势。残差偏差检验的p值为0.001，模型被重新拟合为准泊松模型。

Executive Summary

我们希望确定伯克利大学是否存在性别偏见。对数据的初步分析强烈表明存在这种偏见。然而，这一分析并未进行同类比较。也就是说，它没有比较申请同一系的学生。我们构建了一个模型，该模型包括所有系别、性别和结果，并发现没有显著影响。

为了完整性（尽管效应不显著），我们在下面量化了我们的结论：

估计效应是，每有一位女性被拒绝，就有1.11位男性被拒绝，一旦调整了系别的混杂效应。[注：这相当于说，经过调整后，男性被拒绝的概率估计为女性的1.11倍。]即，在调整系别后，平均而言，约有11%更多的男性被拒绝。比值的置信区间为0.81至1.51。

我们有证据表明，在调整各个科室之前，性别与入院结果之间的关联是显著的（P值≈0）。然而，一旦调整了各个科室，就没有足够的证据表明真实的比例与1不同（P值= 0.55)。

Lecturer Comment

这里发生的情况是，女性倾向于申请录取率较低的部门（可能是法律和医学）。男性则倾向于申请录取率较高的部门（可能是统计学！！）。性别与录取结果之间的关联确实存在，但并非由性别本身引起，而是由于不同性别在部门偏好上的差异所致。

Plots for revealing the deparmental preferences:

Gender vs Acceptance

propn.gender=Berk.tbl[,1]/apply(Berk.tbl,1,sum)

barplot(propn.gender,ylim=c(0,.7), main="Berkeley admission rate by gender", col=c("lightblue", "lightgreen"),xlab="gender",legend.text=c("female", "male"))

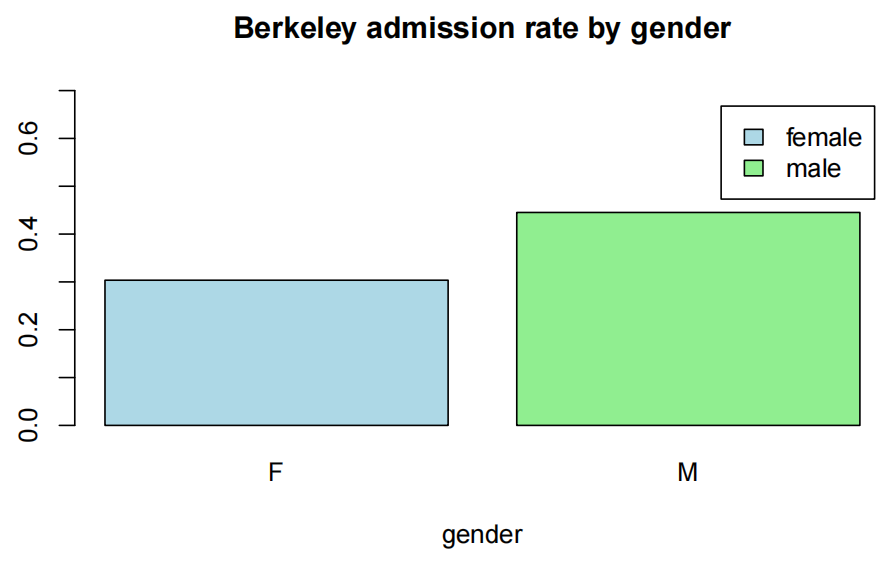
Looking at outcome by department for each gender

BerkByDept = xtabs(Freq ~ Gender + Outcome + Dept, data = Berk.df)

propn.gender.dept=BerkByDept[,1,]/apply(BerkByDept,c(1,3),sum)

barplot(propn.gender.dept, ylim=c(0,.85), main="Berkeley admission rate by dept and gender",col=c("lightblue""lightgreen"),xlab="Department",legend.text=c("female", "male"),beside=T)

Chapter1: Getting started with linear regression

Chapter2: The basics of simple linear regression

Chapter 3: Equivalence of the null linear model and the one-sample t-test(零线性模型的等价性和单样本t检验)

Chapter 4: Fitting curves(曲线) with the linear model

Chapter 5: Linear models with a 2-level categorical (factor) explanatory variable（具有2级分类（因素）解释变量的线性模型）

Chapter 6: Multiplicative（乘法） linear models（指数模型）

Chapter 7: Power law linear models（幂律线性模型，也就是幂指数模型）

Chapter 8: Linear models with both numeric and factor explanatory variables(具有数值和因子解释变量的线性模型)

Chapter 9: Linear models with both numeric and factor explanatory variables（具有数值和因子解释变量的线性模型）

Chapter 10: Multiple linear regression models（多元线性回归模型）

Chapter 11: Linear models with a single factor explanatory variable having three or more levels (One-way analysis of variance)具有三个或更多水平的单因素解释变量的线性模型（单因素方差分析）

Chapter 12: Linear models with two explanatory factor variables (Two-way analysis of variance)具有两个解释因子变量的线性模型（双向方差分析）

Chapter 13: Modelling count data using the Poisson distribution（使用 Poisson 分布对计数数据进行建模）

Chapter 14: Poisson modelling of count data: Two examples（针对GLM-Poisson的两个例题）

Chapter 15: Modelling proportion data using the binomial distribution（用二项式分布对比例数据进行建模）

二元 (伯努利) 数据、优势比 (Odds) 与对数优势比 (Log-odds)

建模对数优势比 (logistic回归)

通过 glm 建模二元响应 (未分组数据)

通过 glm 建模二项响应 (分组数据)

模型解释与推断 (logistic回归)

Chapter 16: Analysis of contingency tables（列联表分析）

引言与分类数据

二项模型分析列联表 (以2x2表示例)

泊松模型分析列联表 (以2x2表示例)

二项与泊松模型的等价性 (特指2x2饱和模型)

泊松模型的优势

优势比率 (Odds Ratio, OR) (可选内容)

卡方检验 (Chi-squared Test for Association) (可选内容)

提交成功

数据分析方法